Практическое занятие № 1 Прогнозирование вероятности наступления чрезвычайных ситуацийЦель: Научиться рассчитывать основные показатели, определяющие вероятность  наступления чрезвычайных ситуаций в течение года.Количественные характеристики риска чрезвычайных ситуаций   представляет собой прогнозирование вероятности её наступления  на величину ожидаемого ущерба У: . (1.1)Вероятности наступления очередной ЧС зависит о времени ожидания , (1.2)где τ> - время ожидания,  - продолжительность протекания самой ЧС, - функция риска. Функция риска является интегральной функцией распределения непрерывной случайной величины, Т-времени ожидания следующей ЧС, поэтому 0 при ; 0 при  . (1.3)Для представления функции риска чаще всего используют показательную и степенную функцию:

---

=1-exp- ; (1.4)

=1- , (1.5)

где  - средняя продолжительность чрезвычайной ситуации.

Функции риска (1.4) соответствует простейшему пуассонову потоку ЧС и быстро достигает насыщения, т.е. значения, близкого к единице. Функция риска (1.5) стремится к единице более медленно и характерна для последовательности редких катастрофических событий.

Параметры функций риска  и определяются путём статистической обработки вариационного ряда эмпирических значений интервалов между смежными ЧС.

Для этого диапазоны изменения  и необходимо разбить на одинаковые частичные интервалы и подсчитать частоты значений этих величин , попадающих в каждый интервал.

Каждому частичному интервалу ставится в соответствие значение  и , равные среднему арифметическому концов этих интервалов. Относительные частоты значений определяются по формуле

---

= , (1.6)

Где,  - объём выборки,m - число частичных интервалов. По относительным частотам периодов ожидания ЧС  вычисляются значения эмпирической функции риска:

. (1.7)

В качестве значений параметров  и берутся их выборочные точечные оценки:

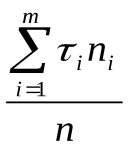= = ; (1.8)

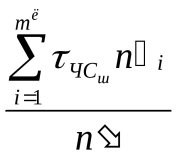= = . (1.9)

Параметр  Функции риска (1,5) определяется по эмпирическим данным методом наименьших квадратов

=1+ , (1.10)

где: A=  (1.11)

B=  (1.12)

Более точно соответствует опытным данным функция риска

---

, минимизирующая сумму квадратов разностей её расчётных и эмпирических значений:

S= min. (1.13)

В формуле риска (1) входит вероятность наступления ЧС за единицу времени, обычно в течении года. Эта вероятность может быть найдена с помощью функции риска:

. (1.14)

Расчет

Выбрать функцию риска и найти вероятность наступления разрушительного урагана по статистическому распределению времени ожидания очередного урагана, приведенному в таблице 1.1 (объём выборки n=20, одно значение   выходит за рамки исследуемого периода и не учитывается,  =(0,01).

Частичные интервалы	2 - 4	4 - 6	6 - 8	8 - 10	10 - 12	12 - 14
	3	5	7	9	11	13
	10	4	1	2	1	1

Решение

1. 
   Найдём относительные частоты значений  и рассчитаем эмпирическую функцию риска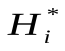 (табл. 1.2)
   

	3	5	7	9	11	13
	0,5	0,2	0,05	0,10	0,05	0,05
	0,5	0,7	0,75	0,85	0,9	0,95

---

2. 
   Найдем среднее значение интервала между двумя смежными ураганами
   

3. 
   Вычислим параметр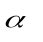  степенной функции риска
   

A= =70.99B= =260.89 =1+ =1.272

4. 
   Запишем функции риска и вычислим их значение в точках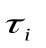 
   

(табл. 1.3) =1-exp(- ),  ( τ)=1-(

	3	5	7	9	11	13
	0,450	0,636	0,757	0,838	0,892	0,927
	0,788	0,815	0,832	0,843	0,851	0,858

5. 
   Для обеих функций риска вычислим сумму квадратов невязок:
   

---

Смотрите также файлы

• Здесь обязательно введите тему или вариант (для кр) .docx

• 9 класс я2 соч 4 Ф. И.docx

• Учитель не позволяет школьникам эмоциональных проявлений, таких как удивление, недовольство, оживление, боязнь и др.docx

• 4тосан бойынша жиынты баалауа арналан тапсырмалар 9 сынып Геометрия.docx

• "Электропривод грузового лифта" по дисциплине.docx