Министерство цифрового развития, связи и массовых коммуникаций

Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное

бюджетное образовательное учреждение высшего образования

Московский технический университет связи и информатики

_________________________________________________________________

Кафедра «Информатика»

Лабораторная работа № 4 по дисциплине Численные методы

«Численное интегрирование»

Выполнил студент группы БИН2109: Зубков М.В.

Проверил: Мацкевич А.Г.

Москва 2023

Цель работы:

В этой лабораторной работе решается задача численного интегрирования.

Индивидуальное задание:

Для решения задачи численного интегрирования выберем функцию подынтегральную функцию, пределы интегрирования и метод интегрирования, согласно варианту №5:

• 
  f(x) = cos(2x) + 2 sin(x) – подынтегральная функция;
  
• 
  a = 1, b = 3 – пределы интегрирования;
  
• 
  m = 2, т.е. метод интегрирования – метод трапеций;
  
• 
  t = 1, т.е. метод интегрирования – метод средних прямоугольников;
  
• 
  h₀ = 0.5 – шаг интегрирования.
  

Вычисление интегралов с шагом h₀ 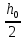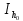и ( и 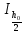) методом трапеций и оценка его погрешности по правилу Рунге

Правило Рунге применяют для вычисления погрешности путём двойного просчёта интеграла с шагами 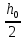и h, при этом погрешность вычисляется по формуле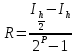

Полагают, что интеграл вычислен с точностью Е, если |R| < E, тогда 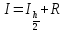, где I – уточненное значение интеграла, p – порядок метода.

---

Вычислим интеграл по формуле трапеций и оценим погрешность интегрирования методом двойного просчета:

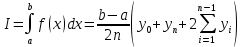, где y_i = f(x_i)

Расчет производился с помощью математического пакета Mathcad и представлен на рисунке 1.



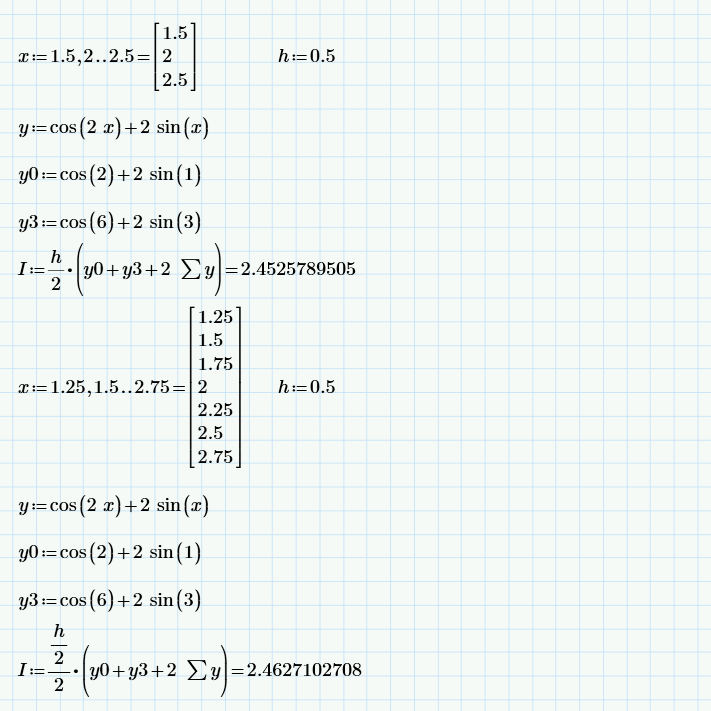
Рисунок 1 – вычисление интеграла методом трапеций

Оценка погрешности:



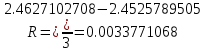
Вычисление интегралов с шагом h₀ и ( и ) методом средних прямоугольников при помощи программы

Ниже представлен программный код, вычисляющий интеграл с заданной точностью.

import math

a = float(input("Введите нижний предел интегрирования: "))
b = float(input("Введите верхний предел интегрирования: "))
eps = float(input("Введите точность: "))

n = 1
I = 0
iterations = 0

while True:
h = (b - a) / n
summa = 0
for i in range(n):
xi = a + i * h + h / 2
fxi = math.cos(2 * xi) + 2 * math.sin(xi)
summa += fxi

I_new = h * summa
iterations += 1
R = (I_new - I) / 3
if abs(R) < eps:
break
else:
I = I_new
n *= 2

print(f"При точности {eps} интеграл равен {I_new}")
print(f"Количество итераций: {iterations}")
print(f"Оценка погрешности: {R}")

На рисунке 2 представлен результат вычисления интеграла программой для точности 10^-2.



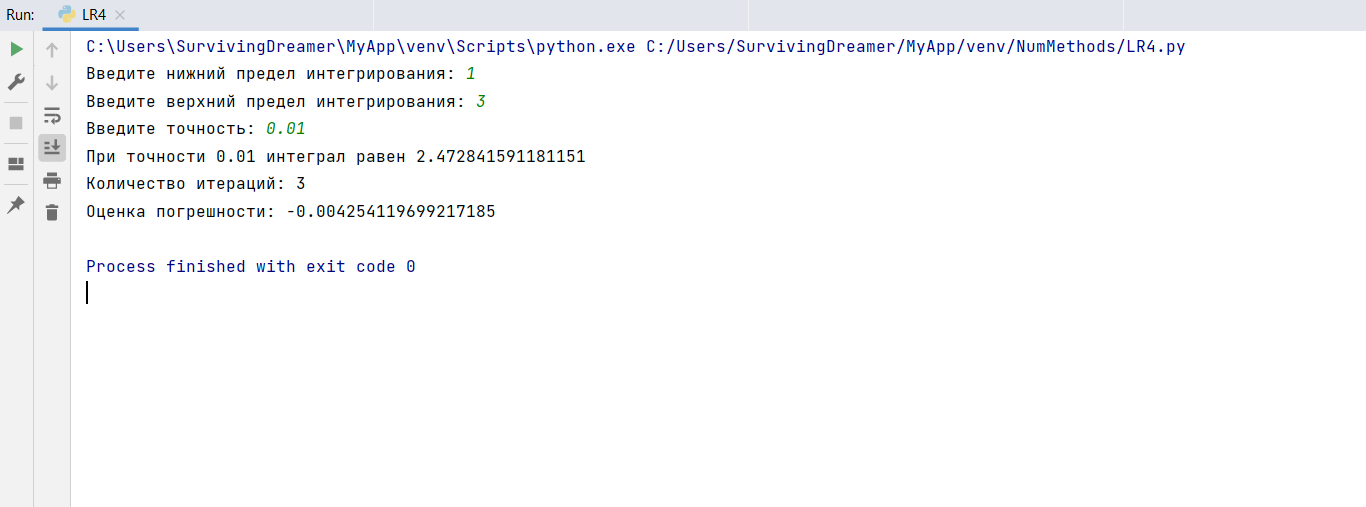
Рисунок 2 – вычисление интеграла с точностью 10^-2

Результаты вычислений интеграла с другими точностями представлены в таблице 1.

Таблица 1 – результаты вычислений интеграла при помози программы

Точность приближения	Значение интеграла	Оценка погрешности	Количество итераций
10-2	2.47284	-0.00425	3
10-3	2.46667	-0.00043	5
10-4	2.46626	-2.77606·10-5	7
10-5	2.46624	-6.94716·10-6	8

---

График зависимости количества итераций от точности приближения представлен на рисунке 3.



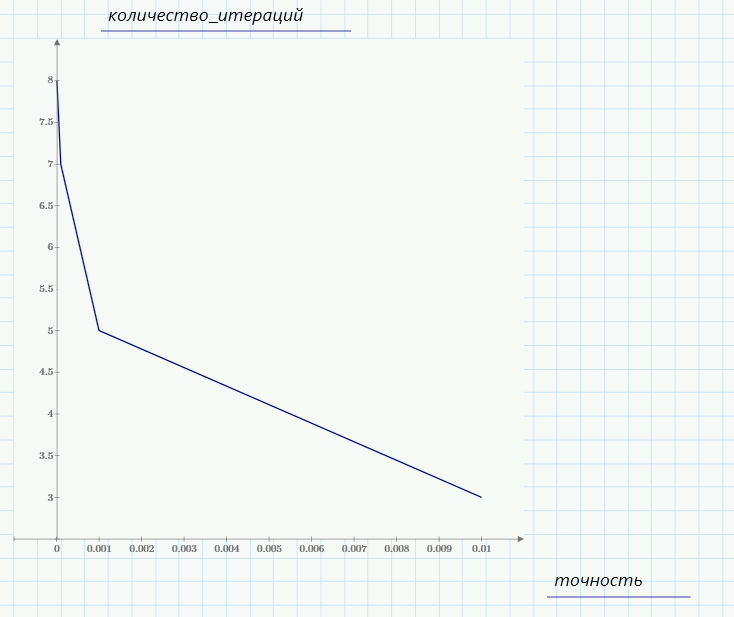
Рисунок 3 – зависимость количества итераций от точности приближения

---

Смотрите также файлы

• Практическая работа 1 Парная регрессия и корреляция по дисциплине Эконометрика.docx

• 1. Основные формы деятельности человека.docx

• Практическое задание 4 Формы, методы и средства в работе по ознакомлению с окружающим миром с детьми с различными нарушениями развития Учебноисследовательское задание.docx

• Группа бэпз 2001.pptx

• Суммативное оценивание за раздел 3С Относительная атомная масса. Простейшие формулы.docx