Файл: Решение Определим ожидаемую доходность из формулы где r i доходность, w i доля в портфеле.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тома Сергей Павлович, группа М-16
1. Найти ожидаемую доходность, если инвестор обладает портфелем акций, который характеризуется следующими показателями: Показать расчет.
| Акции | Доля в портфеле, % | Доходность, % |
| 1 | 20 | 10 |
| 2 | 50 | 20 |
| 3 | 30 | 40 |
Решение:
Определим ожидаемую доходность из формулы:
где Ri – доходность, wi – доля в портфеле, %;
Ответ: ожидаемая доходность портфеля составляет 24%.
2. Используя данные таблицы, рассчитайте коэффициент вариации для акций компаний A и B, если известно, что вероятность варианта 1 для обеих акций составляет 28 %, варианта 2 – 58 %, варианта 3 – 14 %. Оцените риск альтернативных вложений.
| Показатели | Акции компании А | Акции компании В |
| Текущая стоимость, руб. предполагаемый дивиденд, руб.: вариант 1 вариант 2 вариант 3 | 100 23,0 35,6 41,8 | 150 37,2 42,0 51,6 |
Решение:
Определим доходности акций по каждому варианту из формулы:
Ri = di / C
где d – предполагаемый дивиденд в i-ой экономической ситуации; C – текущая стоимость акции.
Результаты оформим в виде таблицы.
| Показатели | Акции компании А | Доходность, % | Акции компании В | Доходность, % |
| Текущая стоимость, руб. предполагаемый дивиденд, руб.: вариант 1 вариант 2 вариант 3 | 100 23,0 35,6 41,8 | 23,0 35,6 41,8 | 150 37,2 42,0 51,6 | 24,8 28,0 34,4 |
Определим ожидаемую доходность из формулы:
где Ri – доходность, в i-ой экономической ситуации; pi – вероятность получения дохода в i-ой экономической ситуации.
Определим дисперсию из формулы:
σ2А1 = (23 – 6,44)2 · 0,28 = 76,79
σ2А2 = (35,6 – 20,65)2 · 0,58 = 129,67
σ2А3 = (41,8 – 5,85)2 · 0,14 = 180,92
σ2В1 = (24,8 – 6,94)2 · 0,28 = 89,27
σ2В2 = (28 – 16,24)2 · 0,58 = 80,21
σ2В3 = (34,4 – 4,82)2 · 0,14 = 122,53
Стандартное отклонение доходности составит:
Коэффициент вариации (V):
VA1 = 8,76 / 6,44 = 1,36
VA2 = 11,39 / 20,65 = 0,55
VA3 = 13,45 / 5,85 = 2,30
VB1 = 9,45 / 6,94 = 1,36
VB2 = 8,96 / 16,24 = 0,55
VB3 = 11,07 / 4,82 = 2,30
Ответ: значения коэффициента вариации позволяют заключить, что на единицу доходности по 2 варианту акций А и В приходится наименьший риск, чем по оставшимся вариантам.
2. Оцените риск по I и II портфелям, состоящим из трех видов ценных бумаг (А, В и С) на основании следующих данных. Определите наименее рисковый.
| | Доля в I портфеле | Доля во II портфеле | Β (показатель рискованности вложений) |
| А | 0,4 | 0,5 | 0,5 |
| В | 0,3 | 0,3 | 3,0 |
| С | 0,3 | 0,2 | 2,0 |
Решение:
Дисперсия портфеля:
где σi – показатель рискованности i-ой ценной бумаги; wi – доля i-ой ценной бумаги в портфеле.
Стандартное отклонение:
Ответ: менее рискованным является портфель II.
3. Инвестиционный аналитик оценил распределение вероятностей доходности акций компании А следующим образом:
| Доходность | Вероятность |
| -5 | 0,1 |
| 0 | 0,2 |
| 5 | 0,3 |
| 10 | 0,3 |
| 15 | 0,1 |
Найти ожидаемую доходность и стандартное отклонение доходности. Показать расчет
Решение:
Определим ожидаемую доходность из формулы:
где Ri – доходность, в i-ой экономической ситуации; pi – вероятность получения дохода в i-ой экономической ситуации.
Определим дисперсию из формулы:
σ2 = (-5 – 5,5)2 · 0,1 + (0 – 5,5)2 · 0,2 + (5 – 5,5)2 · 0,3 + (10 – 5,5)2 · 0,3 + (15 – 5,5)2 · 0,1 = 32,25
Стандартное отклонение доходности составит:
Ответ: ожидаемая доходность равна 5,5%, при этом стандартное отклонение составляет 5,67%.
4. Экспертами предоставлены данные об ожидаемой доходности акций А и В в зависимости от общеэкономической ситуации:
| Экономическая ситуация | Вероятность | Доходность А, % | Доходность В, % |
| Быстрый рост экономики | 0,15 | 17 | 13 |
| Умеренный рост экономики | 0,45 | 14 | 11 |
| Нулевой рост экономики | 0,30 | 8 | 9 |
| Спад | 0,10 | 2 | 7 |
Решение:
Определим ожидаемую доходность из формулы:
где Ri – доходность, в i-ой экономической ситуации; pi – вероятность получения дохода в i-ой экономической ситуации.
Определим дисперсию из формулы:
σ2А = (17 – 11,45)2 · 0,15 + (14 – 11,45)2 · 0,45 + (8 – 11,45)2 · 0,3 + (2 – 11,45)2 · 0,1 = 20,05
σ2В = (13 – 10,3)2 · 0,15 + (11 – 10,3)2 · 0,45 + (9 – 10,3)2 · 0,3 + (7 – 10,3)2 · 0,1 = 3,91
Стандартное отклонение доходности составит:
Коэффициент вариации (V):
VA = 4,47 / 11,45 = 0,39
VB = 1,71 / 10,3 = 0,17
Определим коэффициент ковариации из формулы:
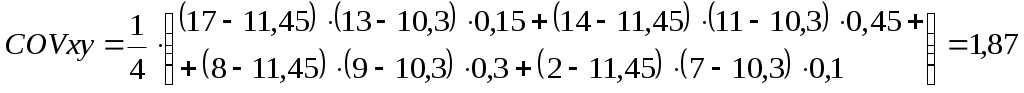
Определим коэффициент корреляции между акциями А и В из формулы:
Значение коэффициента корреляции свидетельствует, что доходности ценных бумаг изменяются в одном направлении с изменением конъюнктуры.
Ответ: ожидаемая доходность акций А равна 11,45%, при этом стандартное отклонение составляет 4,47%; ожидаемая доходность акций В равна 10,3%, при этом стандартное отклонение составляет 1,71%. На единицу доходности акций А приходится примерно вдвое больший риск, чем у акций В. Доходности ценных бумаг изменяются в одном направлении с изменением конъюнктуры.