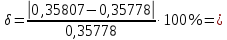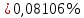Файл: Решение Согласно свойствам логарифмов, подлогарифмическое выражение должно быть больше нуля, т е.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 23.11.2023

Просмотров: 31

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

РАЗДЕЛ 1. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ

Вариант № 6

№ 1.

Найти и изобразить на плоскости область определения функции двух переменных .

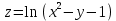Решение:

Согласно свойствам логарифмов, подлогарифмическое выражение должно быть больше нуля, т. е:







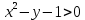
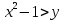
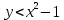
Чтобы изобразить область определения функции, построим сначала график функции 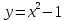(парабола 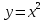, смещенная на 1 масштабную единицу вниз) и выделим относительно оси ординат область, которая располагается ниже графика: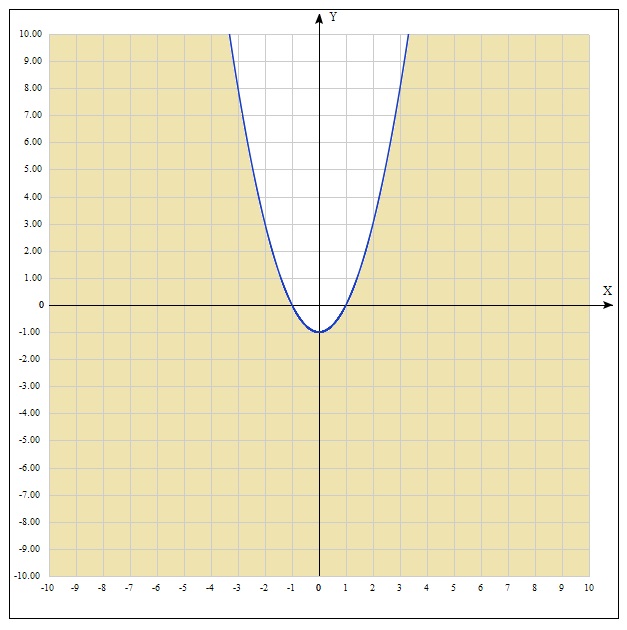



№ 2.

Найти частные производные первого порядка функций двух переменных:

2.1.

















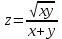
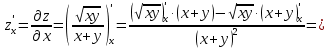
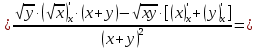
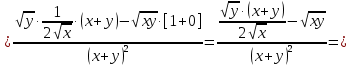
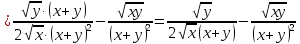
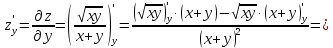
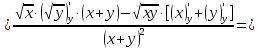
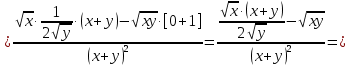
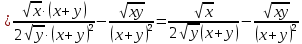
2.2.









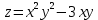
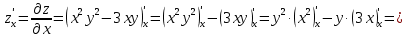
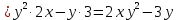
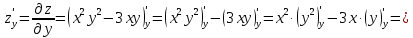
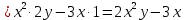
2.3.





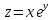
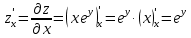
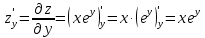
№ 3.

Найти все частные производные второго порядка функции двух переменных:



































=



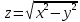
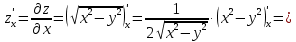
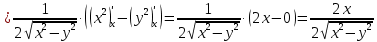
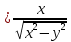
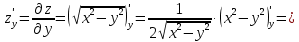
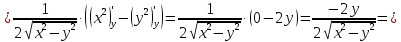
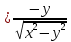
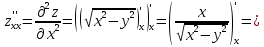
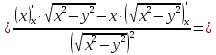
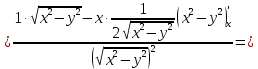
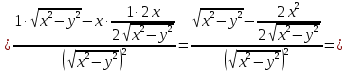
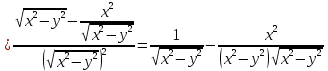
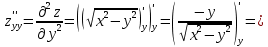
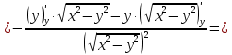
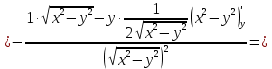
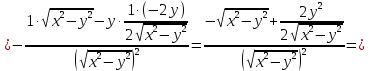
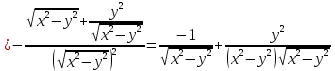
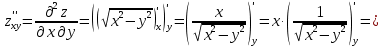
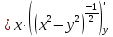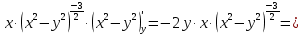
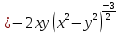
№ 4.

Найти производную функции 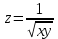в точке 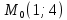в направлении, составляющем с осью абсцисс угол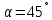

Решение:













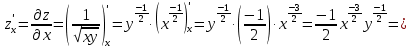
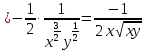
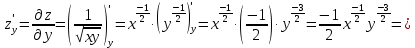
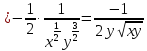
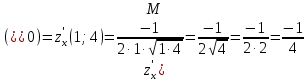
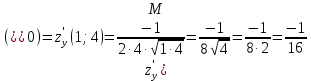
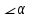– угол с осью абсцисс, ,

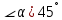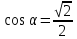
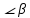– угол с осью абсцисс, ,

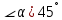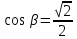
производную функции в точке в направлении, составляющем с осью абсцисс угол , имеет вид: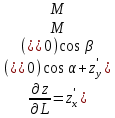



Вычисляем нашу производную по направлению 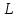в точке :



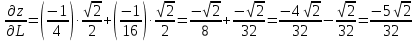
№ 5.

Найти градиент функции 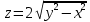в точке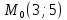













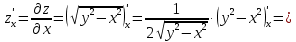
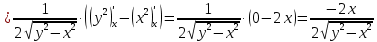
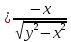
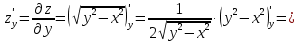
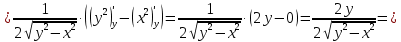
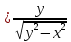
Тогда

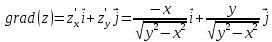
В точке :





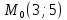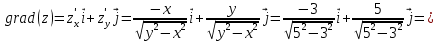
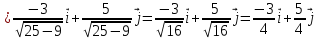
№ 6.

Найти с помощью полного дифференциала приближённое значение выражения .

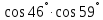Решение:

Введем обозначение функции


,



, ,

, ,

















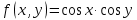
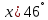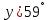
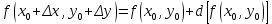
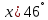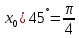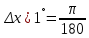
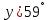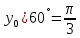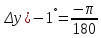
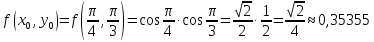
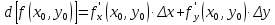
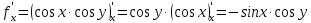
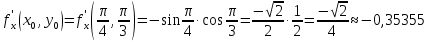
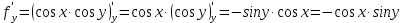
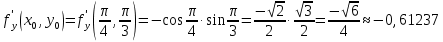
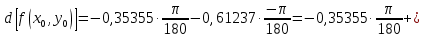
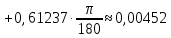
Таким образом,

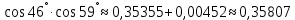
Скалькулированное значение функции:

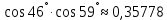
Абсолютная погрешность вычислений:

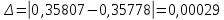
Относительная погрешность вычислений:

Смотрите также файлы