- стандартная схема набора резцов;

- коэффициенты характеризирующие угольный массив принимаются усреднёнными для шахт Донбасса.

Суть увеличения эффективности добычи ОК заключается в следующем.

Из-за невозможности чёткого отслеживания границы раздела порода-уголь и горно-геологических особенностей угольного пласта возможность контролировать зольность добываемого угля позволяет уменьшить расходы на его обогащение, а также на электроэнергию, потребляемую ОК.

На основе изложенных положений составим расчётную схему идентифицируемого объекта.



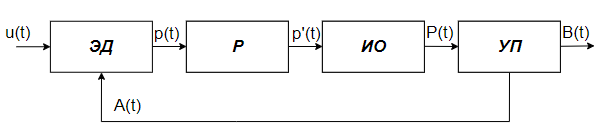
Рисунок 2.1.2 – Расчётная схема идентифицируемого объекта

В этой схеме:

ЭД – электродвигатель;

Р – редуктор;

ИО – исполнительный орган;

УП – угольный пласт;

u(t) – подаваемое напряжение;

p(t) – мощность на выходе ЭД;

p’(t) – мощность на выходе редуктора;

P(t) – сила резания исполнительного органа;

B(t) – количество добываемого угля;

A(t) – сопротивление угля резанию.

---

2.2 ВЫБОР МЕТОДА ИДЕНТИФИКАЦИИ
Наличие расчетной схемы исследуемого объекта позволяет перейти к составлению уравнений математической модели. Как известно, трудоемкость разработки, а часто и корректность результатов моделирования во многом определяются выбранной методикой исследования. Прежде всего, это касается выбора метода структурной идентификации исследуемого объекта.

Принимаем наиболее распространенный подход к разработке математической модели - классический - получение уравнений на основе применения физических законов, описывающих разрушение угольного пласта в процессе добычи шнековым ИО.
2.3 ПОЛУЧЕНИЕ УРАВНЕНИЙ МОДЕЛИ ИССЛЕДУЕМОГО ОБЪЕКТА
Расчёт суммарной силы резания исполнительного органа очистного комбайна при отбойке угля можно по формуле:

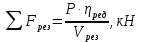, где (1)

P – мощность двигателя, Вт;

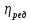– коэффициент полезного действия редуктора ИО;

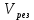– скорость резания, м/мин.

Коэффициент полезного действия редуктора комбайна следует расчитывать по формуле:

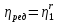, где (2)

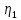– коэффициент полезного действия одного зубчатого зацепления, рекомендуется принимать равным 0,97;

r – количество пар зубчатого зацепления, определяется по кинематической схеме.

Суммарная сила резания на ИО комбайна может быть определена также по формуле:

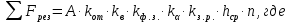(3)

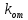– коэффициент отжима, учитывающий уменьшение сопротивляемости резанию по ширине захвата ИО комбайна по сравнению с сопротивляемостью резанию неослабленного горным давлением угольного пласта;

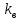– коэффициент, учитывающий изменение силы резания резцами комбайна по сравнению с силой резания стандартным резцом с шириной режущей кромки 20 мм;

---

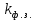– среднее значение коэффициента формы резания забоя ИО комбайна;

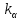– коэффициент, учитывающий изменение силы резания резцами комбайна по сравнению силой резания стандартными резцами установки ДКС-2, имеющий угол резания 50 ̊;

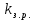– коэффициент, учитывающий увеличение силы резания в следствии затупления резцов;

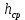– средняя глубина резания ИО комбайна, м;

n – количество резцов, одновременно разрушающих пласт угля одним ИО.

Коэффициент определяется по формуле: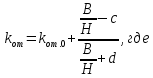

(4)

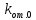– коэффициент, определяемый по таблицам;

B – ширина захвата ИО;

H – мощность вынимаемого пласта;

с и d – коэффициенты, определённые экспериментально и для большинства угольных месторождений с=0.1, d=1.0.

Коэффициент определяется по формуле: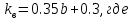

(5)

b – ширина режущей кромки резца, см.

Коэффициент 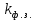является табличным.

Коэффициент 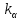является табличным.

Коэффициент 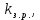в соответствии с особенность резцов зачастую не затупляться, а выламываться из кулаков, рекомендуется принимать в пределах 1.2÷1.3.

Среднюю глубину резания 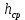, можно выразить из выражения:

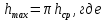(6)

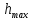– максимальная глубина резания, см.

В свою очередь, 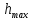находится как: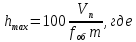

---

(7)

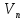– скорость подачи комбайна, м/мин;

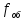– частота вращения рабочего органа, об/мин:

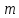– число резцов в линии резания.

Таким образов приравняв равенства 6 и 7:

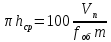(8)

Выразив получим: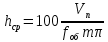

(9)
Приравняв уравнения 1 и 3, получим:
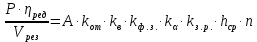(10)

Отсюда:

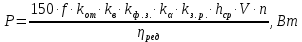(11)

2.4 ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ ИССЛЕДУЕМОГО ОБЪЕКТА
К основным параметрам, характеризующим работу ОК относятся:

- диаметр шнека;

- величина раздвижности исполнительного органа;

- максимальная рабочая скорость подачи;

- тяговое усилие при максимальной скорости подачи;

- номинальное напряжение;

- удельные энергозатраты;

- тип системы подачи.

Кроме того, необходимо выделить такой параметр исследуемого объекта как производительность – это количество добытого полезного ископаемого в единицу времени. Различают теоретическую (показывающую эффективность работы машины при её непрерывной работе, техническую (показывающую эффективность работы машины с учётом её технического несовершенства) и эксплуатационную (показывающую эффективность работы машины с учётом как технического несовершенства, так и потерь с учётом времени на организационные моменты).

3 РЕАЛИЗАЦИЯ РАЗРАБОТАННОЙ МОДЕЛИ СРЕДСТВАМИ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ

3.1 ОБОСНОВАНИЕ МЕТОДИКИ РЕШЕНИЯ МОДЕЛИРУЮЩИХ УРАВНЕНИЙ
В пункте 2.3 была выведена прямая зависимость мощности приводного двигателя шнекового ИО от соотношения порода-уголь. Моделирование данной зависимости будет происходить методом построения семейства характеристик для следующих случаев соотношения порода-уголь: 35/65, 30/70, 25/75, 20/80, 15/85, 10/90 и 5/95.

---

Особенность данного метода является расчёт действительного значения сопротивления угольной массы резанию.

3.2 РАЗРАБОТКА АЛГОРИТМА МОДЕЛИРОВАНИЯ
Блок – схема алгоритма моделирования работы ОК представлена на рисунке 3.2.1



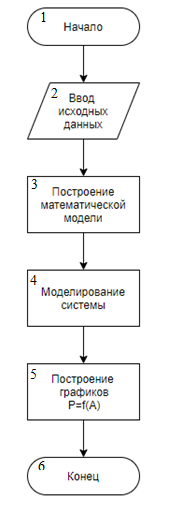
Рисунок 3.2.1 – Блок – схема алгоритма моделирования

В данной блок – схеме:

1 Блок «Начало» - начало программы.

2 Блок «Ввод исходных данных» - ввод необходимых данных.

3 Блок «Построение математической модели» - построение математической модели.

4 Блок «Моделирование системы» - моделирование системы.

5 Блок «Построение графиков P=f(A)» - построение зависимостей мощности приводного двигателя от значения сопротивления горной массы резанию.

6 Блок «Конец» - конец программы.

4 ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ДЛЯ ПРОВЕДЕНИЯ ИССЛЕДОВАНИЙ

4.1 ОЦЕНИВАНИЕ АДЕКВАТНОСТИ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Прежде чем приступить к решению конкретных технических задач, необходимо подтвердить адекватность разработанной математической модели.

Результаты моделирования, приведённые в приложении, показали, что, задаваясь конкретными конечными условиями, полученное семейство графиков характеризует с достаточно высокой точностью изменение мощности приводного двигателя шнекового ИО в зависимости от соотношения порода-уголь, имея допущение об постоянном нормальном состоянии энергообеспечения привода.

Таким образом, можно сделать вывод, что разработанная математическая модель является адекватной.

4.2 ОПТИМИЗАЦИЯ ИССЛЕДУЕМОГО ОБЪЕКТА
Полученная функция P=f(A) имеет вид:



Если детально изучить данную зависимость, то можно выявить следующие:

- данная функция не учитывает в себе возможные изменения в сети электроснабжения, так как на первоначальном этапе задаются параметр номинальной мощности, с помощью которого находится зона «нечувствительности» привода к добываемой угольной массе;

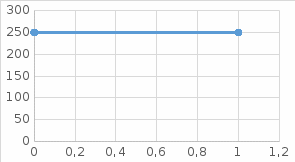
Рисунок 4.2.1 – Зона «нечувствительности» привода

- в состав данной зависимости

---

Смотрите также файлы

• Фпафвапфывап фпафвапфывап фпафвапфывап.docx

• График прохождения летней практики Директор школы Калугина О. А.docx

• Экзаменационные билеты по дисциплине Менеджмент.docx

• Тема 1 эндоскопические методы исследования лорорганов. Клиническая анатомия, физиология и методы исследования наружного и среднего уха..docx

• Реферат по дисциплине Охрана окружающей среды на объектах экономики.pdf