ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 138
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
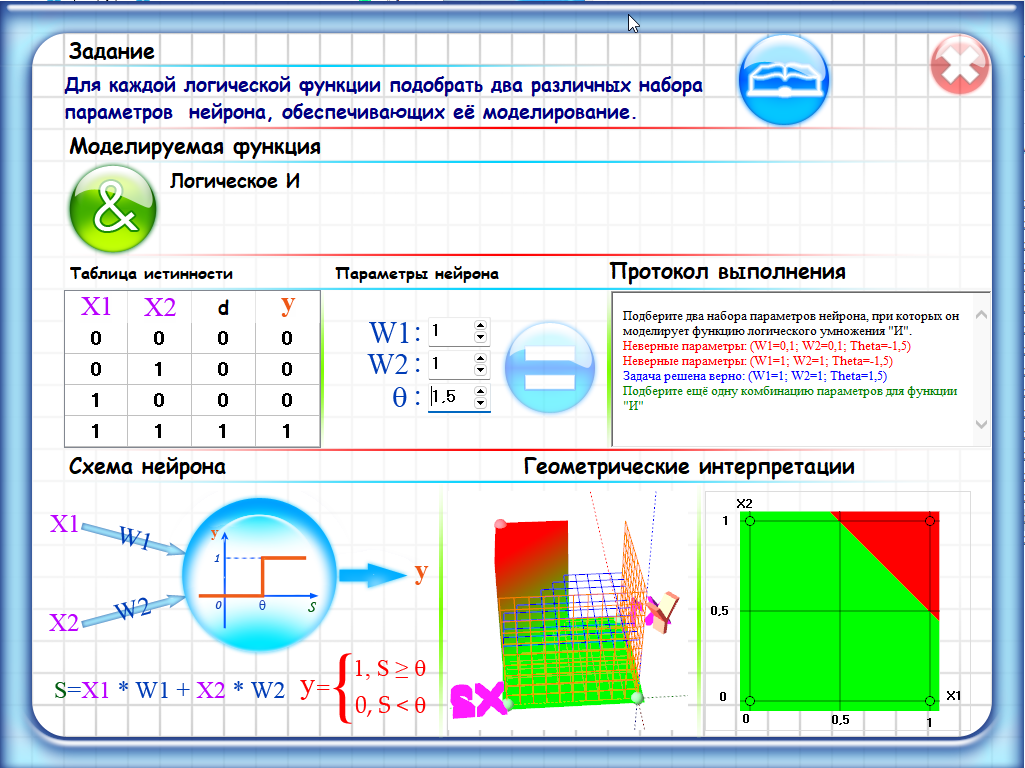


Набор параметров 1:
Веса: w1 = 1, w2 = 1
Порог: theta = 1.5
С использованием этих параметров, нейрон будет выдавать выходное значение 1 только в том случае, если оба входных значения X1 и X2 равны 1, что соответствует функции логического умножения "И".
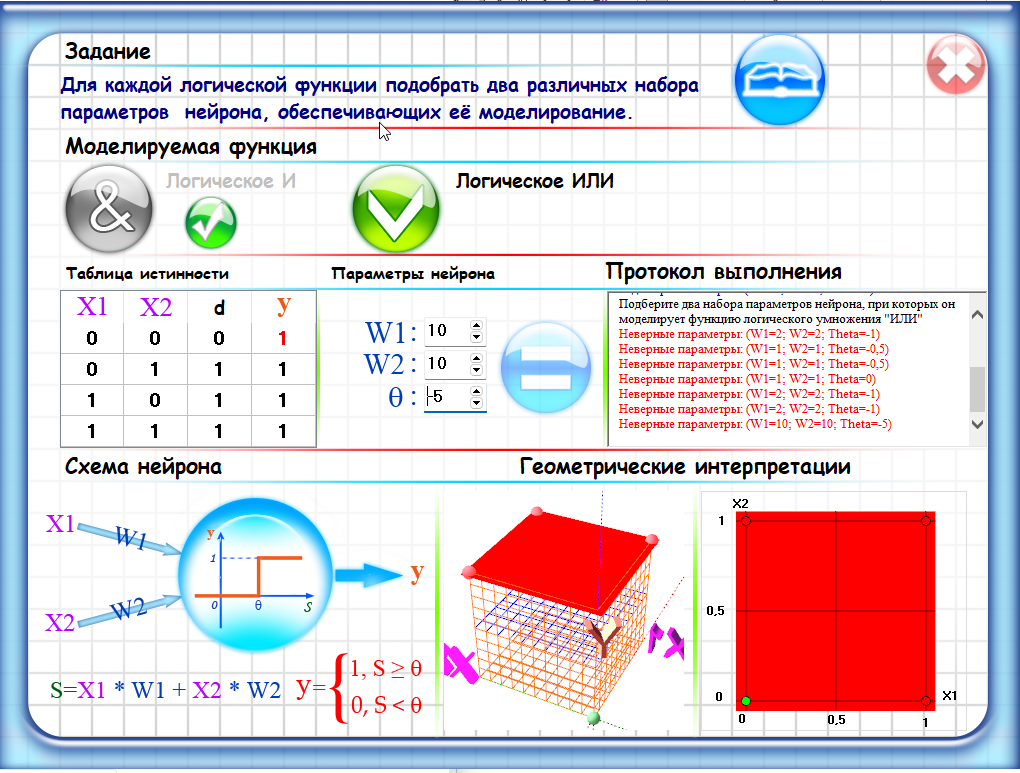
Набор параметров 2:
Веса: w1 = 2, w2 = 2
Порог: theta = 3
С использованием этих параметров, нейрон также будет выдавать выходное значение 1 только в том случае, если оба входных значения X1 и X2 равны 1, что также соответствует функции логического умножения "И". В данном случае, порог выше, так как веса нейрона увеличены, чтобы обеспечить более сильную активацию, если оба входных значения равны 1.
Лаб 2
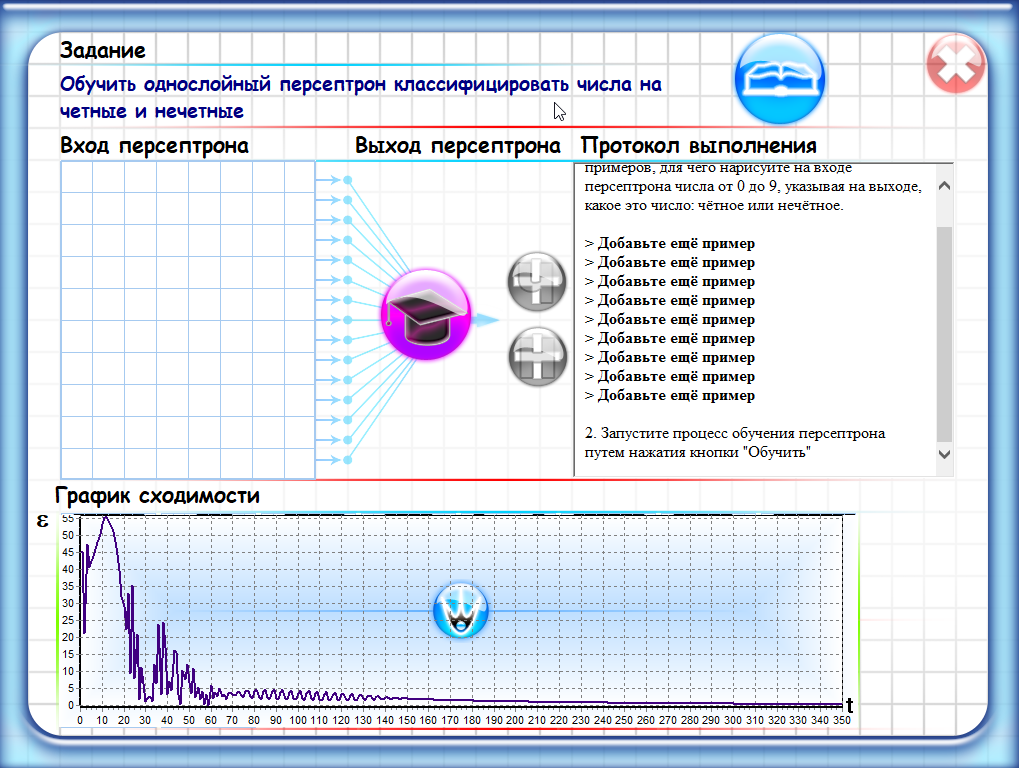
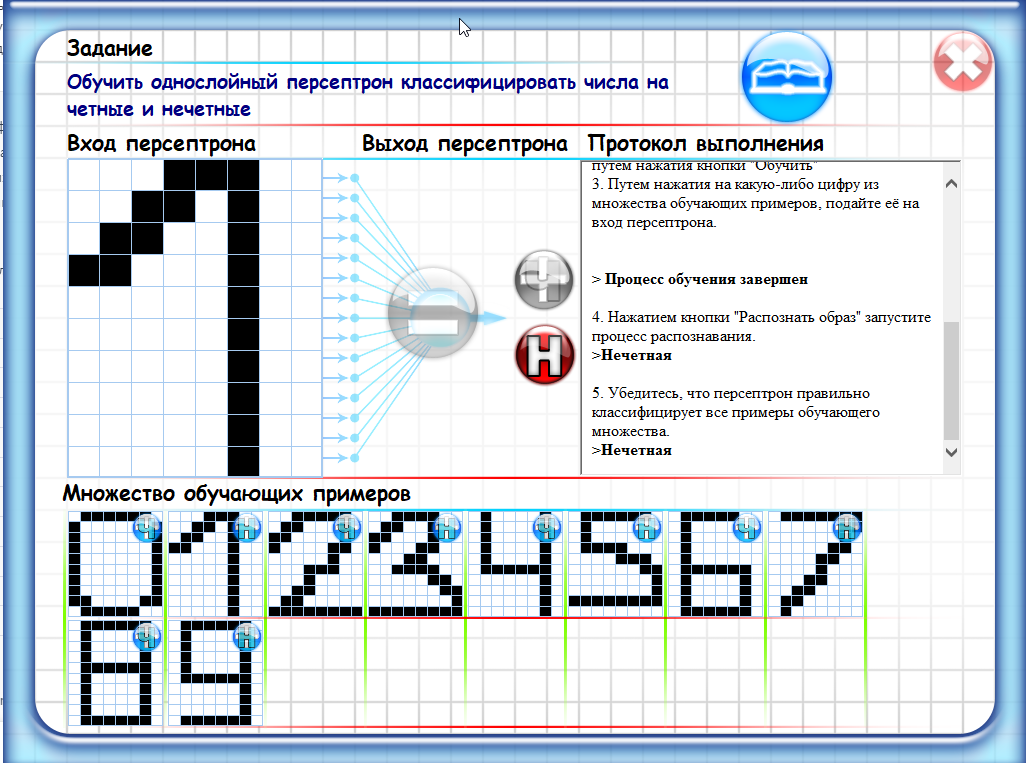
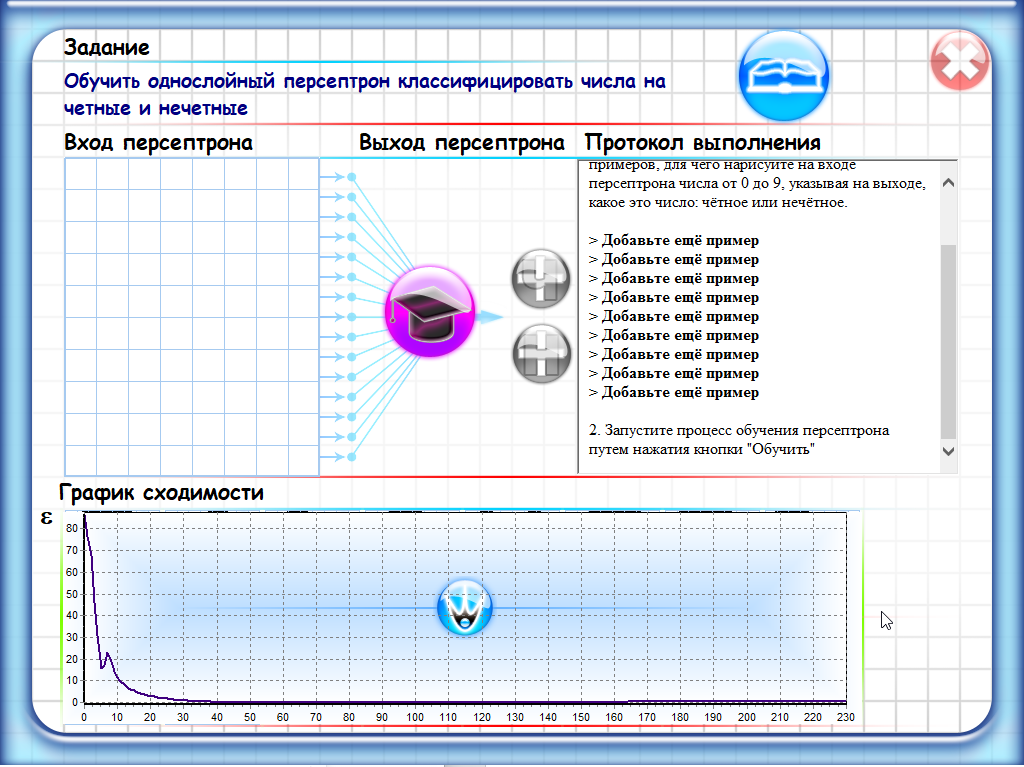
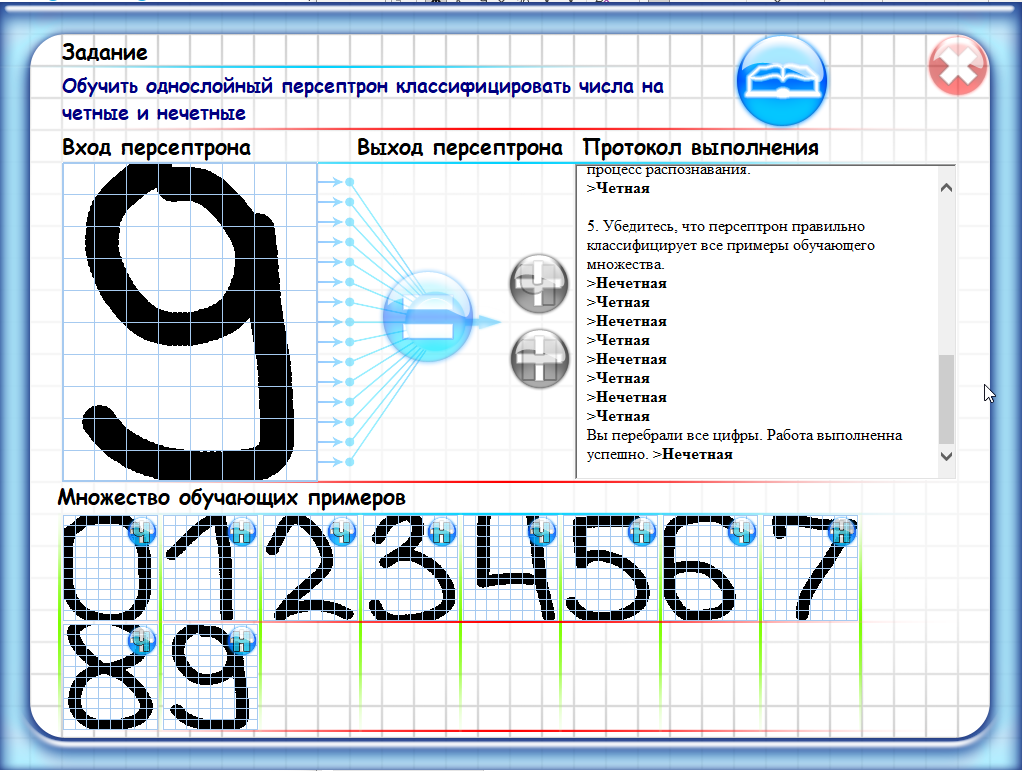
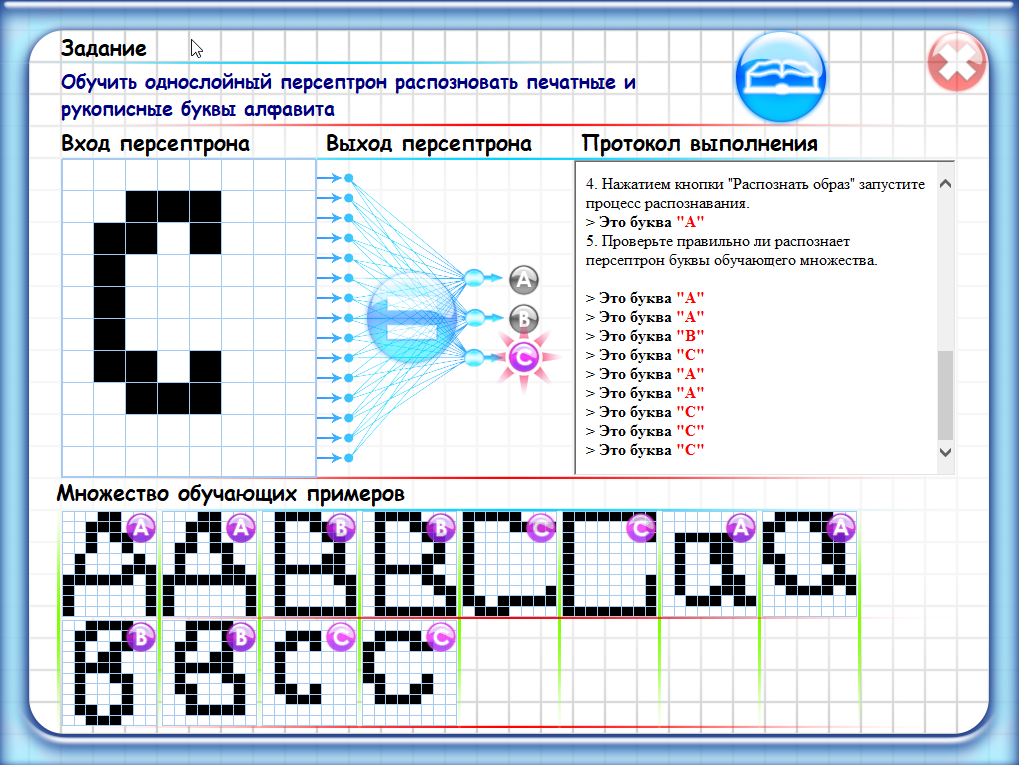
Однослойный персептрон - это простейшая форма искусственной нейронной сети, состоящая из одного слоя нейронов. Каждый нейрон в этой сети принимает на вход набор числовых значений (вектор) и производит выходной сигнал, используя веса, связывающие входные значения и нейрон.
В задаче классификации, например, однослойный персептрон может принимать на вход набор признаков и выдавать на выходе бинарное значение (0 или 1), которое соответствует принадлежности объекта к одному из двух классов.
Обучение однослойного персептрона заключается в настройке весов нейронов таким образом, чтобы минимизировать ошибку классификации на обучающих данных. Этот процесс обычно осуществляется с помощью алгоритма обратного распространения ошибки (backpropagation), который позволяет корректировать веса на каждой итерации обучения.
Лаб 3
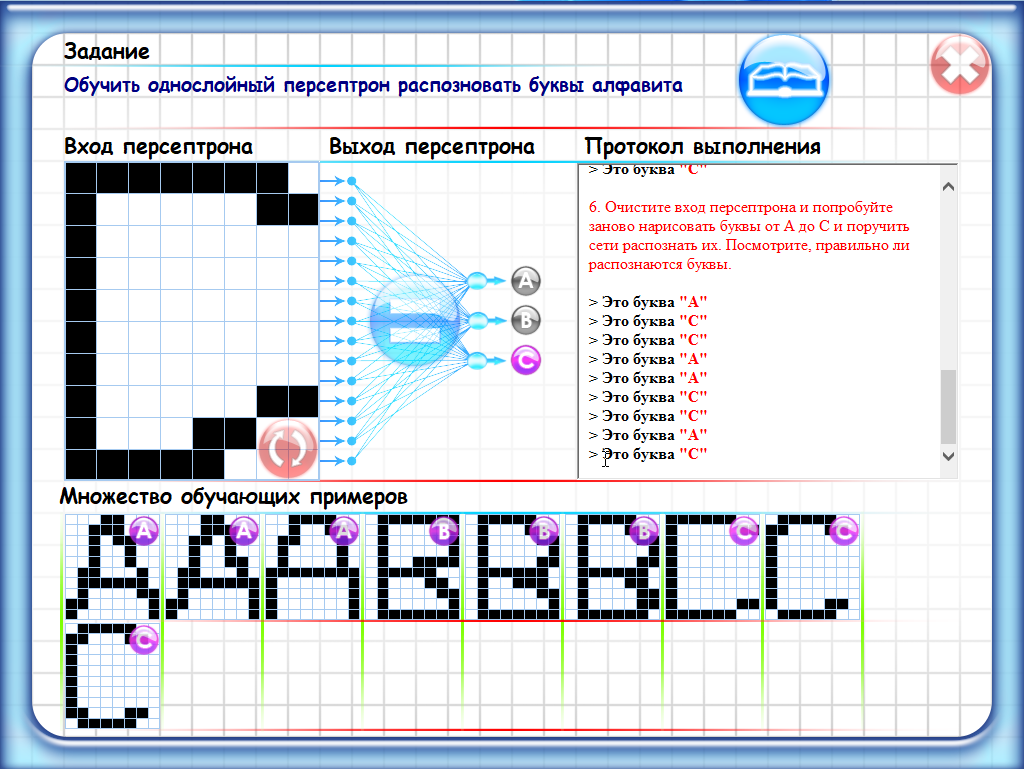
Лаб 4.
Лаб 5.
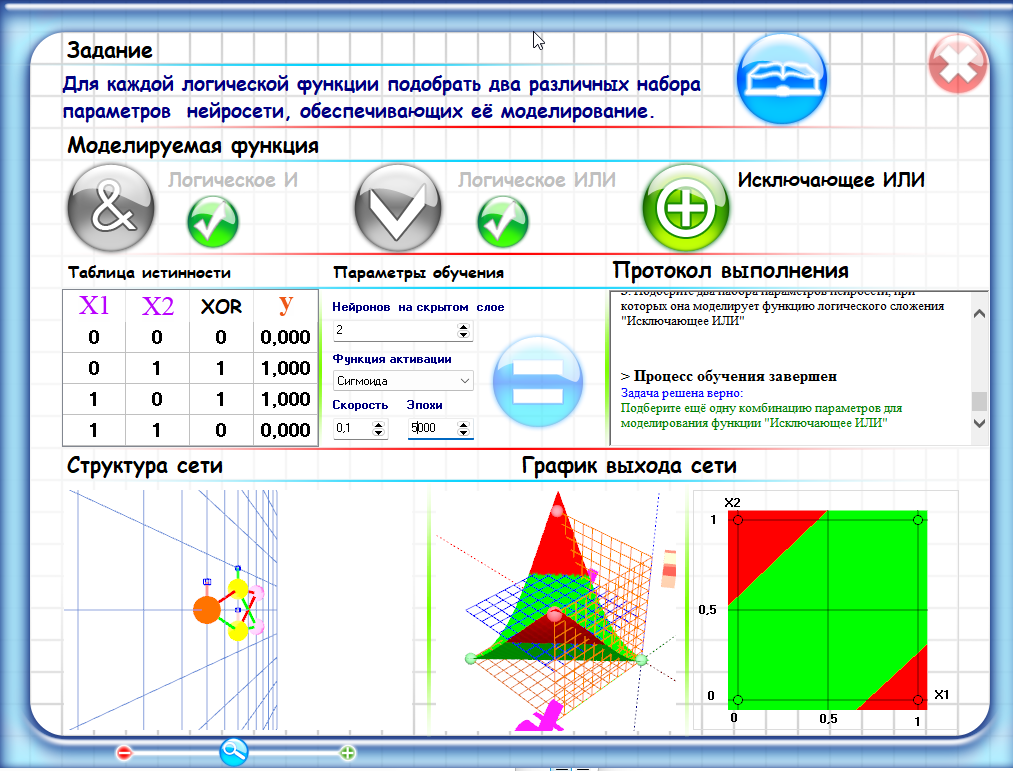

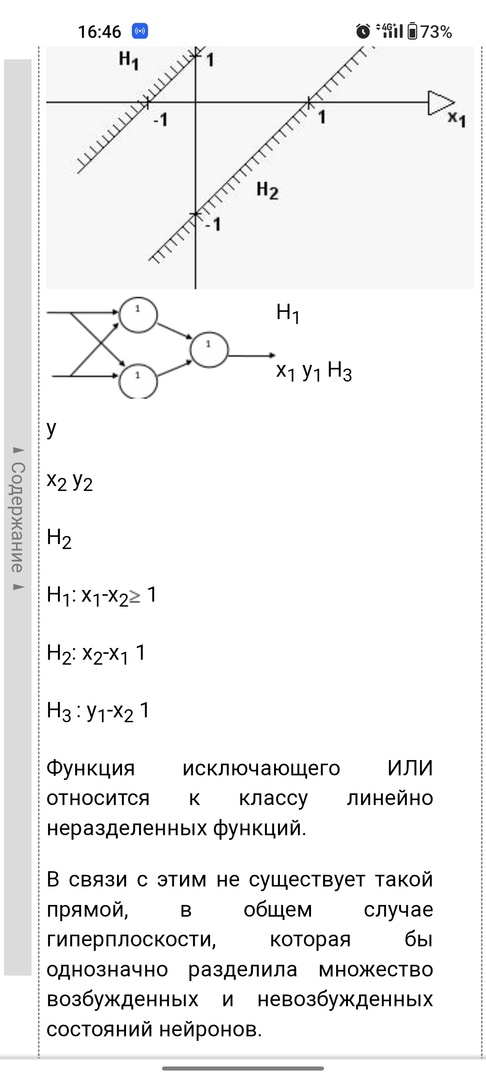
Однонейронный персептрон может моделировать логические функции, которые являются линейно разделимыми, то есть, когда существует линия, которая может разделить классы на плоскости.
Однако логическая функция "исключающее ИЛИ" (XOR) не является линейно разделимой. Это означает, что однонейронный персептрон не может использоваться для моделирования этой функции.
В случае функции XOR нам нужно две линии (гиперплоскости), чтобы разделить примеры на два класса. Это требует более сложной архитектуры сети, которая может иметь несколько скрытых слоев и нелинейные функции активации.
Поэтому, чтобы моделировать логическую функцию "исключающее ИЛИ" (XOR), мы должны использовать более сложные модели нейронных сетей, которые могут иметь несколько слоев и более сложные функции активации.