Отчет по индивидуальной работе №1

«Производная и дифференциал. Приложения производной».

Перечень вопросов

1. 
   Понятие производной от функции.
   
2. 
   Производная сложной функции.
   
3. 
   Основные правила дифференцирования.
   
4. 
   Производные основных элементарных функций.
   
5. 
   Логарифмическое дифференцирование.
   
6. 
   Параметрически заданные функции, их дифференцирование.
   
7. 
   Дифференциал и производные первого и высших порядков.
   
8. 
   Применение производной при вычислении предела (правила Лопиталя)
   
9. 
   Условие монотонности функции.
   
10. 
    Понятие экстремума функции. Необходимое условие существование экстремума.Первое достаточное условие экстремума. Второе достаточное условие экстремума.
    
11. 
    Наибольшее и наименьшее значение функции на отрезке.
    
12. 
    Выпуклость графика функции, точки перегиба. Достаточное условие выпуклости графика функции.
    
13. 
    Асимптоты графика функции.
    

1)Производная функции в точке x₀ равна угловому коэффициенту ка­сательной к графику функции, проведенной в точке с абсциссой x₀.

2) Производная сложной функции равна произведению производной внешней функции на производную от внутренней функции.

3) Рассмотрим основные правила дифференцирования.

Если функции  дифференцируемы в точке , то сумма, разность, произведение и частное этих функций (частное при условии, что ) также дифференцируемы в этой точке и имеют место следующие формулы:

1. 
   
   
2. 
   
   
3. 
   ;
   
4. 
   .
   

---

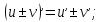
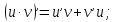
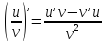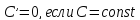4)  Степенная функция: (xⁿ)` =nx^n-1.

2. Показательная функция: (a^x)` =a<sup>x</sup>lna(в частности, (е<sup>x</sup>)` = е^x).

3. Логарифмическая функция:  (в частности, (lnx)` = 1/x).

4. Тригонометрические функции:

(sinх)` =cosx

(cosх)` = -sinx

(tgх)` = 1/cos²x

(ctgх)` = -1/sin²x

5. Обратные тригонометрические функции:



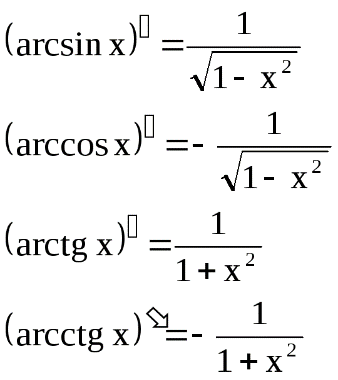
5) В ряде случаев для нахождения производной целесообразно заданную функцию сначала прологарифмировать (по умолчанию имеется в виду натуральный логарифм). Затем найти производную от этого логарифма и по ней отыскать производную от заданной функции. Такой прием называется логарифмическим дифференцированием.

Метод логарифмического дифференцирования позволяет легко найти производную показательно-степенной функции вида

Прологарифмируем обе части функции и преобразуем выражение:

.

Теперь дифференцируем уравнение, как неявно заданную функцию:

;

;

;

;

Так как  , то окончательно получаем:

.

6)

7) Пусть y = f(x) дифференцируема на множестве X1⊆D(f) . Тогда на X1 определена f ′(x). Функцию f ′(x) называют также первой производной функции f(x) (или производной первого порядка функции f(x)). Если f ′(x) дифференцируема на некотором множестве X2⊆X1, то (f ′(x)) ′ называют второй производной функции y = f(x) (или производной второго порядка функции f(x) )

8) В задачах по пределам часто встречаются неопределенные отношения 

---

или  , а также приводимые к ним   и некоторые другие. Быстро раскрыть такие неопределенности помогает следующее правило Лопиталя:

и т.д.,

т.е. отношение функций заменяется отношением их производных до тех пор, пока неопределенность не исчезнет. Очень важно запомнить, что при отсутствии неопределенности правило Лопиталя применять нельзя.

9) Условия монотонности функции

• 
  (Критерий монотонности функции, имеющей производную на интервале) Пусть функция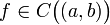  непрерывна на 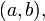и имеет в каждой точке 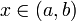производную  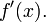Тогда
  

 не убывает на  тогда и только тогда, когда

 не возрастает на  тогда и только тогда, когда

10)

Определение.

Точка

x0 называется точкой

локального максимума

---

функции f (x) , если существует такая окрестность точки x0 , что для всех х из этой окрестности f (x) ≤ f (x0 ).

Определение. Точка x0 называется точкой локального минимума функции f (x) , если существует такая окрестность точки x0 , что для всех х из этой окрестности f (x) ≥ f (x0 ).

• 
  Необходимое условие существования экстремума функции: если х = х₀ - точка экстремума, то f ^/(x₀) =0 или f ^/(x₀) не существует.
  

Точки, в которых f ^/(x₀) обращается в нуль или не существует, называется критическими.

• 
  Достаточное условие существования экстремума функции: если функция y=f(x) непрерывна в точке х = х₀ и ее окрестности, дифференцируема в этой окрестности, кроме, быть может, самой точки, и производная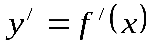  при переходе через точку х = х₀ меняет свой знак, то функция имеет экстремум при х = х_{0 .}
  

11) Пусть функция у = f (х) непрерывна на отрезке [a, b]. Как известно, такая функция на этом отрезке достигает наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке отрезка [a, b], либо на границе отрезка.

Для нахождения наибольшего и наименьшего значений функции на отрезке [a, b] необходимо:

1)найти критические точки функции в интервале (a, b);

2)вычислить значения функции в найденных критических точках;

3) вычислить значения функции на концах отрезка, то есть при x= а и х = b;

4)из всех вычисленных значений функции выбрать наибольшее и наименьшее.

12) График функции  , дифференцируемой на интервале

---

, является на этом интервалевыпуклым, если график этой функции в пределах интервала  лежит не выше любой своей касательной (рис. 1).

График функции  , дифференцируемой на интервале , является на этом интервалевогнутым, если график этой функции в пределах интервала  лежит не ниже любой своей касательной (

Точкой перегиба графика функции  называется точка , разделяющая промежутки выпуклости и вогнутости.

Теорема о достаточном условии вогнутости (выпуклости) графика функции

1) Если для дважды дифференцируемой функции   то график этой функции будет вогнутым в данном промежутке.

2) Если же   то график функции будет выпуклым в этом промежутке.

13) Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой

---

Смотрите также файлы

• 1. Вершины сетевой модели типа Работа Дуга отображают .pdf

• Автономная некоммерческая организация высшего образования московский международный университет совместный рабочий график (план) проведения с 27. 06. 2022 24. 07. 2022.docx

• Методические указания по выполнению курсовой работы по дисциплине Теоретические основы электротехники для обучающихся направления подготовки.pdf

• Программа Открой себя Программа Открой себя.pptx

• Группа 12 (23. 01. 09 Машинист локомотива) Задание по дисциплине оп. 04 Материаловедение для дистанционного обучения Задания выполняются в отдельной тетради, тетрадь подписывается (Ф. И., группа, предмет). Форма оценивания темы.docx