Файл: Сетевое планирование и график Гантта Выбрав вариант задания из таблицы 1, соответствующий первой букве фамилии студента или слушателя, выполнить нижеследующее.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 70
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Находим полный резерв RПi-j = Tпj-ti-j-Tрi
RП(1,2) = 10-10-0 = 0
RП(1,3) = 15-5-0 = 10
RП(1,4) = 22-8-0 = 14
RП(2,3) = 15-3-10 = 2
RП(2,5) = 21-11-10 = 0
RП(2,6) = 33-15-10 = 8
RП(3,4) = 22-7-13 = 2
RП(3,6) = 33-6-13 = 14
RП(4,6) = 33-11-20 = 2
RП(5,6) = 33-12-21 = 0
RП(5,9) = 61-7-21 = 33
RП(6,7) = 43-10-33 = 0
RП(6,8) = 51-6-33 = 12
RП(7,8) = 51-8-43 = 0
RП(7,9) = 61-15-43 = 3
RП(8,9) = 61-10-51 = 0
Свободный резерв времени также можно найти и по формуле RCi-j = Tпi-ti-j-Tрi
RC(1,2) = 10-10-0 = 0
RC(1,3) = 13-5-0 = 8
RC(1,4) = 20-8-0 = 12
RC(2,3) = 13-3-10 = 0
RC(2,5) = 21-11-10 = 0
RC(2,6) = 33-15-10 = 8
RC(3,4) = 20-7-13 = 0
RC(3,6) = 33-6-13 = 14
RC(4,6) = 33-11-20 = 2
RC(5,6) = 33-12-21 = 0
RC(5,9) = 61-7-21 = 33
RC(6,7) = 43-10-33 = 0
RC(6,8) = 51-6-33 = 12
RC(7,8) = 51-8-43 = 0
RC(7,9) = 61-15-43 = 3
RC(8,9) = 61-10-51 = 0
Независимый резерв времени также можно найти и по формуле RНi-j = Tрj-ti-j-Tпi
RН(1,2) = 10-10-0 = 0
RН(1,3) = 13-5-0 = 8
RН(1,4) = 20-8-0 = 12
RН(2,3) = 13-3-10 = 0
RН(2,5) = 21-11-10 = 0
RН(2,6) = 33-15-10 = 8
RН(3,4) = 20-7-15 = -2
RН(3,6) = 33-6-15 = 12
RН(4,6) = 33-11-22 = 0
RН(5,6) = 33-12-21 = 0
RН(5,9) = 61-7-21 = 33
RН(6,7) = 43-10-33 = 0
RН(6,8) = 51-6-33 = 12
RН(7,8) = 51-8-43 = 0
RН(7,9) = 61-15-43 = 3
RН(8,9) = 61-10-51 = 0
Таблица 2 - Анализ сетевой модели по времени
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Ранние сроки: начало tijР.Н. | Ранние сроки: окончание tijР.О. | Поздние сроки: начало tijП.Н. | Поздние сроки: окончание tijП.О. | Резервы времени: полный RijП | Независимый резерв времени RijН | Частный резерв I рода, Rij1 | Частный резерв II рода, RijC |
| (1,2) | 0 | 10 | 0 | 10 | 0 | 10 | 0 | 0 | 0 | 0 |
| (1,3) | 0 | 5 | 0 | 5 | 10 | 15 | 10 | 8 | 10 | 8 |
| (1,4) | 0 | 8 | 0 | 8 | 14 | 22 | 14 | 12 | 14 | 12 |
| (2,3) | 1 | 3 | 10 | 13 | 12 | 15 | 2 | 0 | 2 | 0 |
| (2,5) | 1 | 11 | 10 | 21 | 10 | 21 | 0 | 0 | 0 | 0 |
| (2,6) | 1 | 15 | 10 | 25 | 18 | 33 | 8 | 8 | 8 | 8 |
| (3,4) | 2 | 7 | 13 | 20 | 15 | 22 | 2 | -2 | 0 | 0 |
| (3,6) | 2 | 6 | 13 | 19 | 27 | 33 | 14 | 12 | 12 | 14 |
| (4,6) | 2 | 11 | 20 | 31 | 22 | 33 | 2 | 0 | 0 | 2 |
| (5,6) | 1 | 12 | 21 | 33 | 21 | 33 | 0 | 0 | 0 | 0 |
| (5,9) | 1 | 7 | 21 | 28 | 54 | 61 | 33 | 33 | 33 | 33 |
| (6,7) | 4 | 10 | 33 | 43 | 33 | 43 | 0 | 0 | 0 | 0 |
| (6,8) | 4 | 6 | 33 | 39 | 45 | 51 | 12 | 12 | 12 | 12 |
| (7,8) | 1 | 8 | 43 | 51 | 43 | 51 | 0 | 0 | 0 | 0 |
| (7,9) | 1 | 15 | 43 | 58 | 46 | 61 | 3 | 3 | 3 | 3 |
| (8,9) | 2 | 10 | 51 | 61 | 51 | 61 | 0 | 0 | 0 | 0 |
Следует отметить, что кроме полного резерва времени работы, выделяют еще три разновидности резервов. Частный резерв времени первого вида R1 - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R1 находится по формуле:
R(i,j)= Rп(i,j) - R(i)
Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле:
R(i,j)= Rп(i,j) - R(j)
Значение свободного резерва времени работы указывает на расположение резервов, необходимых для оптимизации.
Независимый резерв времени Rн работы (i,j) - часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле:
R(i,j)= Rп(i,j)- R(i) - R(j)
Критический путь: (1,2)(2,5)(5,6)(6,7)(7,8)(8,9)
Продолжительность критического пути: 61
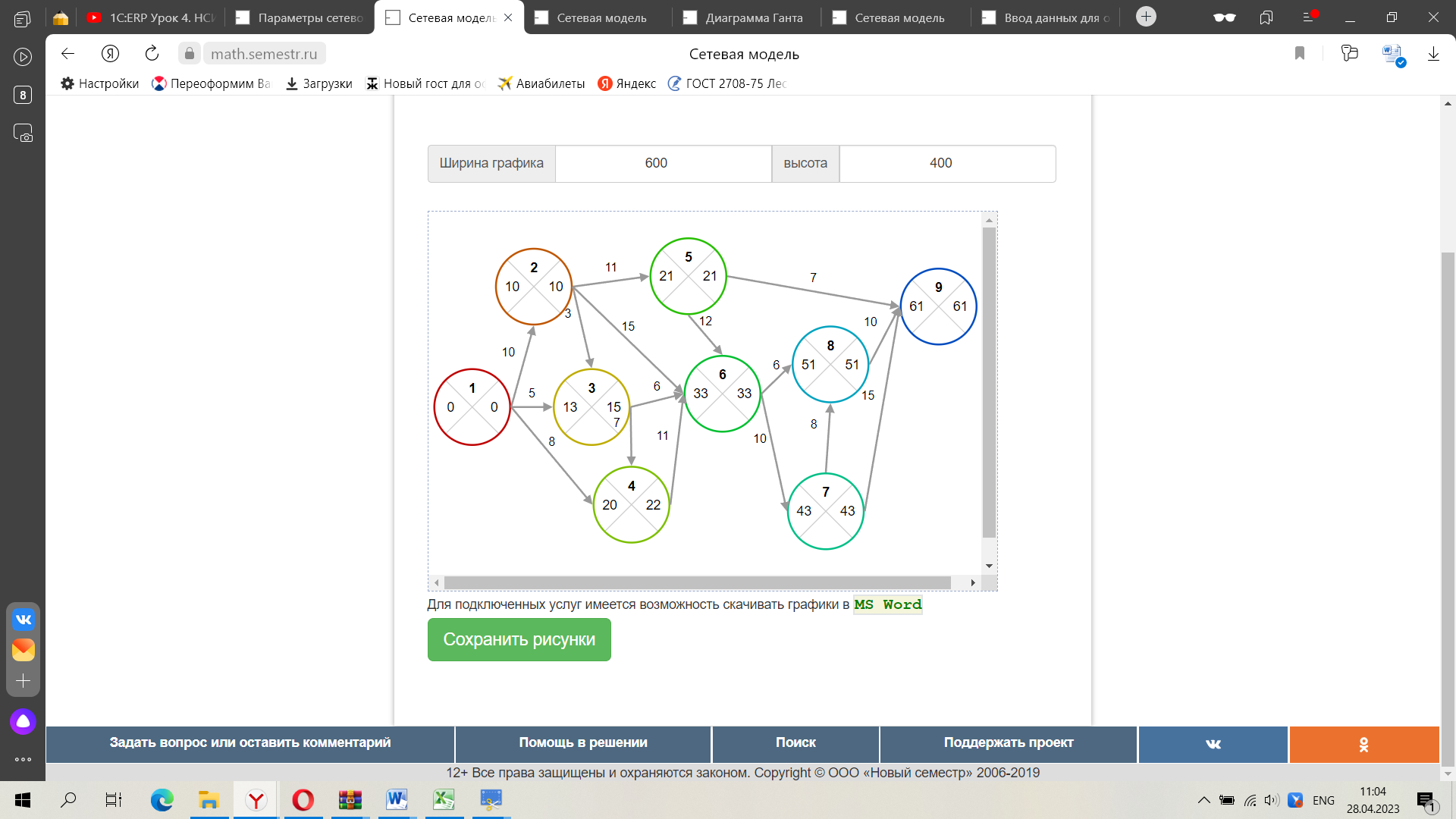
Рис. Сетевой график
Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:
Kc = npab / ncob
где Kc – коэффициент сложности сетевого графика; npab – количество работ, ед.; ncob – количество событий, ед.
Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.
Kc = 16 / 9 = 1.78
Поскольку 1.51 < Kc < 2, то сетевой график является средней сложности.
Коэффициентом напряженности КH работы Pi,j называется отношение продолжительности несовпадающих (заключенных между одними и теми же событиями) отрезков пути, одним из которых является путь максимальной продолжительности, проходящий через данную работу, а другим – критический путь:
где t(Lmax) – продолжительность максимального пути, проходящего через работу Pi,j, от начала до конца сетевого графика; tkp – продолжительность (длина) критического пути; t1kp – продолжительность отрезка рассматриваемого максимального пути, совпадающего с критическим путем.
Коэффициент напряженности КH работы Pi,j может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности КH работы Pi,j, тем сложнее выполнить данную работу в установленные сроки. Чем ближе Кн работы Pi,j к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу.
| Работа | Путь | Максимальный путь, t(Lmax) | Совпадающие работы | t1kp | Расчет | КH |
| (1,2) | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | - | - |
| (1,3) | (1,3)(3,4)(4,6)(6,7)(7,8)(8,9) | 51 | (6,7)(7,8)(8,9) | 28 | (51-28)/(61-28) | 0.697 |
| (1,4) | (1,4)(4,6)(6,7)(7,8)(8,9) | 47 | (6,7)(7,8)(8,9) | 28 | (47-28)/(61-28) | 0.576 |
| (2,3) | (1,2)(2,3)(3,4)(4,6)(6,7)(7,8)(8,9) | 59 | (1,2)(6,7)(7,8)(8,9) | 38 | (59-38)/(61-38) | 0.913 |
| (2,5) | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | - | - |
| (2,6) | (1,2)(2,6)(6,7)(7,8)(8,9) | 53 | (1,2)(6,7)(7,8)(8,9) | 38 | (53-38)/(61-38) | 0.652 |
| (3,4) | (1,2)(2,3)(3,4)(4,6)(6,7)(7,8)(8,9) | 59 | (1,2)(6,7)(7,8)(8,9) | 38 | (59-38)/(61-38) | 0.913 |
| (3,6) | (1,2)(2,3)(3,6)(6,7)(7,8)(8,9) | 47 | (1,2)(6,7)(7,8)(8,9) | 38 | (47-38)/(61-38) | 0.391 |
| (4,6) | (1,2)(2,3)(3,4)(4,6)(6,7)(7,8)(8,9) | 59 | (1,2)(6,7)(7,8)(8,9) | 38 | (59-38)/(61-38) | 0.913 |
| (5,6) | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | - | - |
| (5,9) | (1,2)(2,5)(5,9) | 28 | (1,2)(2,5) | 21 | (28-21)/(61-21) | 0.175 |
| (6,7) | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | - | - |
| (6,8) | (1,2)(2,5)(5,6)(6,8)(8,9) | 49 | (1,2)(2,5)(5,6)(8,9) | 43 | (49-43)/(61-43) | 0.333 |
| (7,8) | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | - | - |
| (7,9) | (1,2)(2,5)(5,6)(6,7)(7,9) | 58 | (1,2)(2,5)(5,6)(6,7) | 43 | (58-43)/(61-43) | 0.833 |
| (8,9) | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) | 61 | - | - |
Вычисленные коэффициенты напряженности позволяют дополнительно классифицировать работы по зонам. В зависимости от величины Кн выделяют три зоны: критическую (Кн > 0,8); подкритическую (0,6 < Кн < 0,8); резервную (Кн < 0,6).
Сократим критический путь на 1 день за минимальную доплату к ранее найденной стоимости в нормальном режиме выполнения работ.
Прежде всего, установим, за какую минимальную доплату можно завершить комплекс работ за 60 дня вместо 61 дней. Сокращение срока на день возможно только за счет уменьшения на один день продолжительности критического пути. Это, в свою очередь, можно достичь, ускоряя на день какие-либо критические работы, лежащие на этих путях. Для того, чтобы установить какие критические работы в совокупности ускорять дешевле, нужно вычислить средние стоимости 1 дня ускорения всех выявленных критических работ.
Рассмотрим критическую работу (1,2), ее можно ускорить с 10 до 0 дней, доплатив за это 0 д.е. Отсюда среднюю стоимость дня ускорения работы найдем по формуле:
Рассмотрим критическую работу (2,5), ее можно ускорить с 11 до 0 дней, доплатив за это 0 д.е.
Рассмотрим критическую работу (5,6), ее можно ускорить с 12 до 0 дней, доплатив за это 0 д.е.
Рассмотрим критическую работу (6,7), ее можно ускорить с 10 до 0 дней, доплатив за это 0 д.е.
Рассмотрим критическую работу (7,8), ее можно ускорить с 8 до 0 дней, доплатив за это 0 д.е.
Рассмотрим критическую работу (8,9), ее можно ускорить с 10 до 0 дней, доплатив за это 0 д.е.
После проведенных расчетов, очевидно, что уменьшение продолжительности критического пути (1,2)(2,5)(5,6)(6,7)(7,8)(8,9) на один день следует проводить за счет ускорения работы (1,2) с доплатой 0 д.е.
В итоге самым дешевым вариантом для сокращения срока на 1 день является ускорение на один день работ [(1,2)], что приведет к новому критическому сроку 60 дня с минимальной доплатой 0 = 0 д.е.
Выполним запланированные ускорения работ [(1,2)] и сделаем перерасчет временных характеристик сетевого графика.
Отсюда итоговая стоимость составит 0 + 0 = 0 д.е.
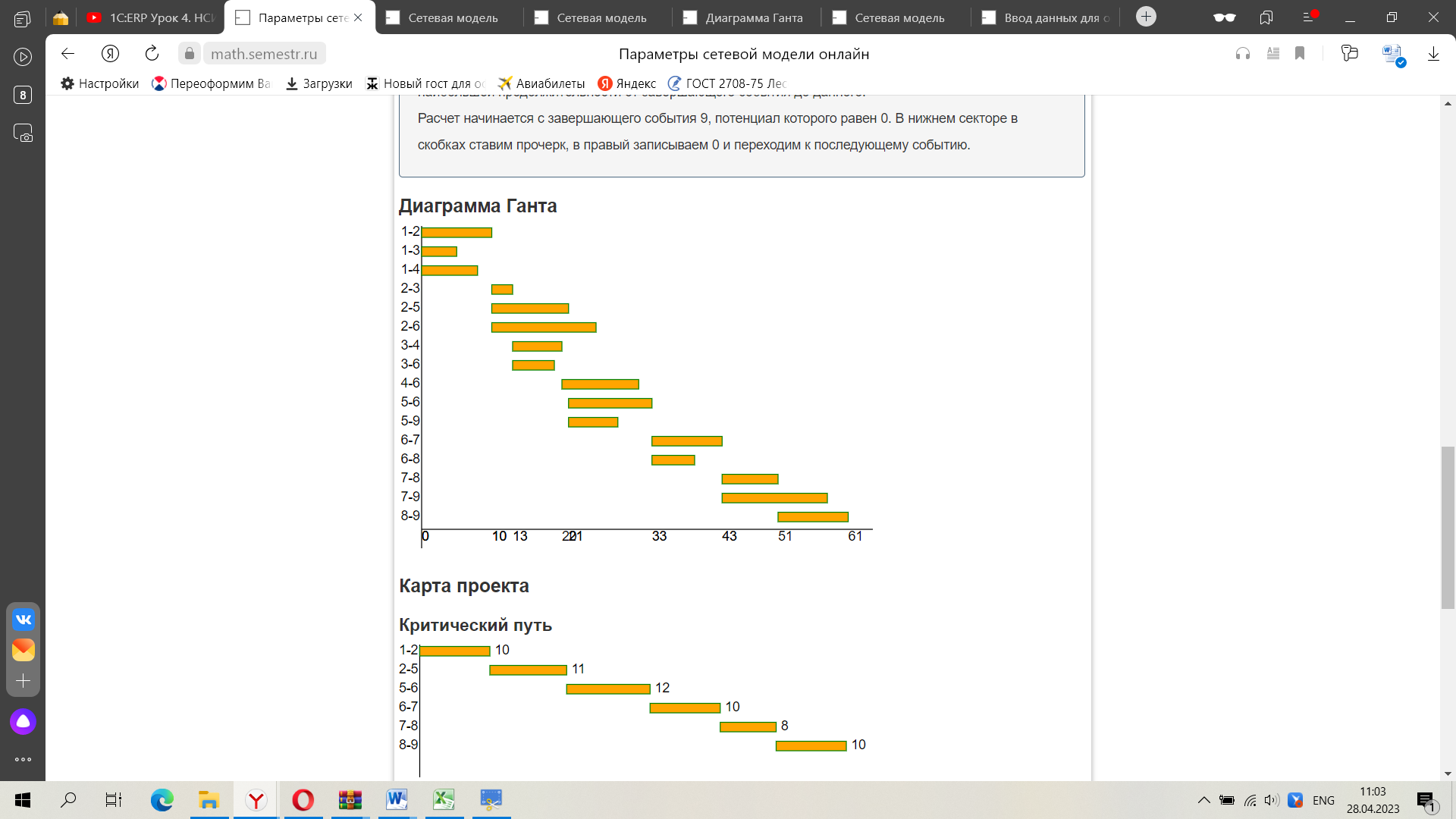
Рис. Диаграмма Ганта