Файл: Спецификация контрольноизмерительных материалов для проведения итоговой контрольной работы по математике в 11 классе.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 24.11.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Спецификация
контрольно-измерительных материалов для проведения
итоговой контрольной работы по математике
в 11 классе
1. Назначение контрольно-измерительных материалов.
Контрольно-измерительные материалы (КИМ) позволяют установить уровень освоения учащимися 11 класса Федерального компонента государственного образовательного стандарта среднего (полного) общего образования.
2. Документы, определяющие содержание контрольных измерительных материалов
Содержание контрольной работы определяется на основе:
-
Федерального компонента государственного стандарта среднего (полного) общего образования по математике на профильном уровне (приказ МОиН РФ от 05.03.2004г. № 1089, ред. от 31.01.2012 года), -
Рабочей программы по математике на базовом уровне (приказ МБОУ «СОШ № от № ).
3. Подходы к отбору содержания, разработке структуры контрольных измерительных материалов.
Подходы к отбору содержания, разработке структуры КИМ, содержание заданий разработано по основным темам учебного предмета «Математика».
Работа состоит из трех частей:
Часть 1 (базовый уровень) содержит 6 заданий базового уровня, среди которых задания 1-3 с выбором ответа.
Часть 2 (повышенный уровень) содержит 2 задания с развернутым ответом.
Часть 3 (высокий уровень) содержит 1 задание с развернутым ответом, подразумевающее нахождение наибольшего и наименьшего значения функции на заданном отрезке.
Таблица 1. Распределение заданий по частям работы
| Часть работы | Количество заданий | Максимальный первичный балл | Процент максимального первичного балла за выполнение заданий данной части от максимального первичного балла за всю работу, равного 100 | Тип задания |
| Часть 1 | 6 | 13 | 52 | С выбором ответа |
| Часть 2 | 2 | 7 | 28 | С развернутым ответом |
| Часть 3 | 1 | 5 | 20 | С развернутым ответом |
| Итого | 9 | 25 | 100 | |
Распределение заданий КИМ по содержанию и видам деятельности
Таблица 2. Распределение заданий по темам курса математики
| № | Название разделов/тем | Число заданий | Максимальный балл |
| 1 | Тригонометрические формулы | 1 | 2 |
| 2 | Производная и её геометрический смысл | 1 | 2 |
| 3 | Тригонометрические функции | 1 | 2 |
| 4 | Элементы комбинаторики | 1 | 2 |
| 5 | Производная и её геометрический смысл | 1 | 2 |
| 6 | Объемы тел | 1 | 3 |
| 7 | Решение тригонометрических уравнений | 1 | 3 |
| 8 | Интеграл | 1 | 4 |
| 9 | Применение производной к исследованию функций | 1 | 5 |
| | итого | 9 | 25 |
Продолжительность работы 2 урока (90 минут).
Система оценивания выполнения заданий и работы в целом
| Отметка | «2» | «3» | «4» | «5» |
| Баллы | 0-12 | 13-18 | 19-23 | 24-25 |
-
Обобщенный план варианта КИМ по МАТЕМАТИКЕ.
Уровни сложности заданий: Б – базовый, П – повышенный, В – высокий.
| № | Проверяемые элементы содержания | Проверяемые требования (умения) | Коды проверяемых требований (умений) (по КТ) | Коды проверяемых элементов содержания (по КЭС) | Уровень сложности задания | Максимальный балл за выполнение задания |
| 1 | Синус, косинус, тангенс углов | Уметь находить значения синуса косинуса, тангенса угла на основе определений, с помощью калькулятора и таблиц. | 1.3 | 1.2.1 1.2.2 | Б | 2 |
| 2 | Производные некоторых элементарных функций | Использовать определение производной при нахождении производных элементарных функций | 3.2 | 4.1.1 - 4.1.5 | Б | 2 |
| 3 | Область определения и множество значений тригонометрических функций | Находить область определения и область значения тригонометрических функций | 3.1 | 3.3.5 | Б | 2 |
| 4 | Комбинаторные задачи | Решать простейшие задачи из теории вероятности | 6.1 | 6.1.1, 6.1.2 | Б | 2 |
| 5 | Геометрический смысл производной | Применять понятие производной при решении физических задач | 3.2 | 4.1.1 | Б | 2 |
| 6 | Объемы тел | Решать задачи на вычисление объемов | 4.2 | 5.5.7 | Б | 3 |
| 7 | Решение тригонометрических уравнений | Уметь решать простейшие тригонометрические уравнения | 2.1 | 2.1.4 | П | 3 |
| 8 | Наибольшее и наименьшее значения функций | Применять правило нахождения наибольшего и наименьшего значения функции на отрезке и на интервале | 3.3 | 3.2.6 | П | 4 |
| 9 | Площадь криволинейной трапеции | Изображать криволинейную трапецию, ограниченную заданными кривыми. Находить площадь криволинейной трапеции | 4.1, 3.2 | 4.3.1, 4.3.2 | В | 5 |
Итоговая контрольная работа по математике для 11 класса
Вариант 1
I уровень. В заданиях 1–3 укажите букву верного ответа.
1.Вычислить
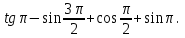
А. 1; Б 0; В. -1. Г. 2
2. Найдите производную функции
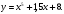
А.
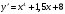 Б.
Б. 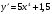 В.
В. 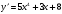 Г.
Г. 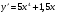
3. Найдите множество значений функции
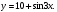
А. [–1; 1] Б.
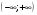 В.
В. 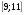 Г.
Г. 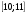
4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
5. Тело движется прямолинейно по закону х(t) = 3t4 - 2t3 +1 (x в метрах, t в секундах). Найдите его скорость в момент времени t = 2.
6. Радиус основания конуса равен 4, высота в два раза больше радиуса. Найдите объем конуса. (π=3)
II уровень
7. Решите уравнение
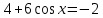
8. Найдите наименьшее значение функции у= х3 – х2 – 40х + 3 на отрезке
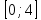
III уровень
9. Вычислить площадь фигуры ограниченной линиями: у = х+3 , у = -х2 +8х -7.
Вариант 2
I уровень. В заданиях 1–3 укажите букву верного ответа.
1. Вычислить
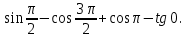
А. 1; Б 0; В. -1. Г. 2
2. Найдите производную функции
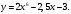
А.
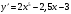 Б.
Б. 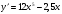 В.
В. 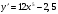 Г.
Г. 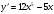
3. Найдите множество значений функции
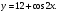
А. [–1; 1] Б.
 В.
В. 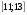 Г.
Г. 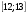
4. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 5 очков. Результат округлите до сотых.
5. Тело движется прямолинейно по закону х(t) = 2t4 - 3t2 – 5t(x в метрах, t в секундах). Найдите его скорость в момент времени t = 4c
6. Радиус основания цилиндра равен 6, а высота в три раза меньше радиуса. Найдите объем цилиндра. (π=3)
II уровень
7. Решите уравнение
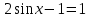
8. Найдите наибольшее значение функции у= х3 +2х2 -4х +4 на отрезке
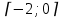
III уровень
-
Вычислить площадь фигуры ограниченной линиями: у = 8х - х2-2, у = х+8.
Ключ
| № задания | 1 вариант | 2 вариант |
| 1 | А | Б |
| 2 | Б | В |
| 3 | В | В |
| 4 | 0,17 | 0,11 |
| 5 | 72 | 483 |
| 6 | 128 | 216 |
| 7 | x=π+ 2πn | x=π/2+πn |
| 8 | -109 | 12 |
| 9 | 4.5 | 4,5 |