Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "Уфимский государственный нефтяной технический университет"
Кафедра "Математика"

Отчет по лабораторной работе №4
По дисциплине "Математические методы обработки результатов экспериментов"
"Однофакторный дисперсионный анализ"
Вариант №??
Выполнил: студент гр. ???- ??-01 ?????????
Проверил: доцент Лазарев В.А.
Уфа 2023

Дано:Для четырех уровней фактора F экспериментально получены значения исследуемой величины Х.

	F1	F2	F3	F4
1	45	47	56	30
2	68	52	29	45
3	47	45	37	40
4	56	54	36	69
5	58	61	38	15

Проверить гипотезу о влиянии фактора F на значения Х.
Задача:

1. 
   Вычислить групповые средние и общую среднюю.
   
2. 
   Вычислить общую, факторную и остаточную суммы квадратов отклонений от общей средней.
   
3. 
   Вычислить общую, факторную и остаточную дисперсии.
   
4. 
   Проверить гипотезу о равенстве групповых средних.
   

На количественный признак X воздействует фактор

---

F, имеющий

р=4 дискретных уровней и на каждом уровне проведено одинаковое число опы­тов q=5.
Теоретическое обоснование:
1) Общую среднюю можно получить как среднее арифметическое групповых средних:



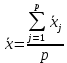
На разброс групповых средних относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы.

Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной 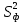, а вторая – остаточной .
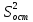2)С целью учета этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:



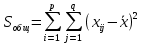
и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:



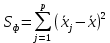
Последнее выражение получено путем замены каждой варианты в выражении 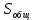групповой средней для данного фактора.

Остаточная сумма квадратов отклонений получается, как разность:


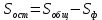
3)Для определения общей выборочной дисперсии необходимо 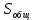разделить на число измерений pq: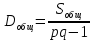



а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на :



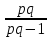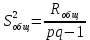
Соответственно, для несмещенной факторной выборочной дисперсии:



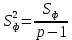
,где 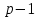- число степеней свободы несмещенной факторной выборочной дисперсии.

---

С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:



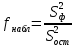
Так как отношение двух выборочных дисперсий и распределено по закону Фишера-Снедекора, то полученное значение 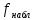сравнивают со значением функции распределения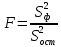



в критической точке 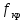, соответствующей выбранному уровню значимости α.

Если 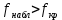, то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.

Для расчета 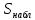и 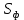могут быть использованы также формулы: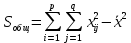




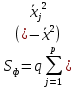
Решение:
Находим групповые средние:

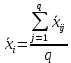
N	П1	П2	П3	П4
1	45	47	56	30
2	68	52	29	45
3	47	45	37	40
4	56	54	36	69
5	58	61	38	15
∑	274	259	196	199
xср	54.8	51.8	39.2	39.8

---

Обозначим р - количество уровней фактора (р=4). Число измерений на каждом уровне одинаково и равно q=5.

В последней строке помещены групповые средние для каждого уровня фактора.

Общая средняя вычисляется по формуле:



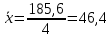
Для расчета по формуле составляем таблицу квадратов вариант:

N	П21	П22	П23	П24
1	2025	2209	3136	900
2	4624	2704	841	2025
3	2209	2025	1369	1600
4	3136	2916	1296	4761
5	3364	3721	1444	225
∑	15358	13575	8086	9511

S_общ = 15358 + 13575 + 8086 + 9511 - 5 • 4 • 46.4² = 3470.8

Находим по формуле:

S_ф = 5(54.8² + 51.8² + 39.2² + 39.8² - 4 • 46.4²) = 975.6

Получаем :



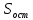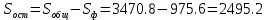
Определяем факторную дисперсию:



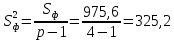
и остаточную дисперсию:



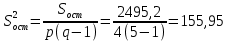
Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.

---

Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.

Оценка факторной дисперсии меньше оценки остаточной дисперсии, поэтому можно сразу утверждать справедливость нулевой гипотезы о равенстве математических ожиданий по слоям выборки.

Иначе говоря, в данном примере фактор F не оказывает существенного влияния на случайную величину.

Проверим нулевую гипотезу:

H0: «средние значения Х равны для всех значений фактора».

Находим .



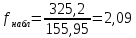
Для уровня значимости α=0.05, чисел степеней свободы 3 и 16 находим из таблицы распределения Фишера-Снедекора.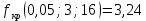

.

В связи с тем, что 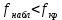, нулевую гипотезу о равенстве групповых средних принимаем. Другими словами, групповые средние в целом различаются не значимо, гипотезу о существенном влиянии фактора F на результаты экспериментов отклоняем.

---

Смотрите также файлы

• Ответы к экзамену по ит.docx

• Мониторинг инвестиционной деятельности регионов рф.ppt

• Практическая работа 2 Проект управленческого решения и перечень поручений.docx

• Білімділік масаты.docx

• "Бастау" олимпиадасы логикалы есептер 3 сынып.docx