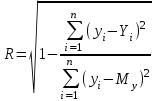Файл: Лабораторная работа 6 Нахождение коэффициентов аппроксимирующих функций.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №6
«Нахождение коэффициентов аппроксимирующих функций»
Цель: Научиться подбирать аппроксимирующие функции при обработке статистических данных.
Задание 1. Методом наименьших квадратов по табличным данным найти аппроксимирующие (приближаемые) функции, то есть регрессии: линейную, квадратичную, кубическую, показательную.
Задание 2. В каждом случае найти коэффициент и индексы корреляции. Указать функцию лучшей аппроксимации.
Задание 3. Построить линии регрессии на одной плоскости вместе с исходными данными.
Задание 4*. Разработать программу, позволяющую подбирать коэффициенты перечисленных выше аппроксимирующих функций, рассчитывать коэффициенты и индексы корреляции.
Варианты заданий.
-
Исходные данные товарооборота от дохода населения.

-
Исходные данные уровня благосостояния населения от уровня занятости.

-
Исходные данные товарооборота от дохода населения.

-
Исходные данные уровня занятости от заработной платы населения.

-
Исходные данные уровня рождаемости от уровня заработной платы населения.

-
Исходные данные объема выпускаемой продукции от числа занятых рабочих.

-
Исходные данные товарооборота между Россией и Японией за 5 лет (млрд долларов) (http://www.polpred.ru).

-
Исходные данные товарооборота между Россией и Японией за 5 лет (млрд дол.) (http://www.polpred.ru).

-
Некоторые исходные показатели экономического развития КНР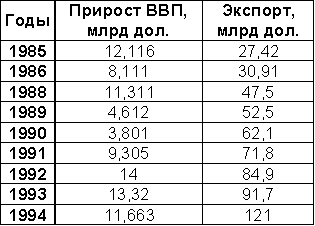
-
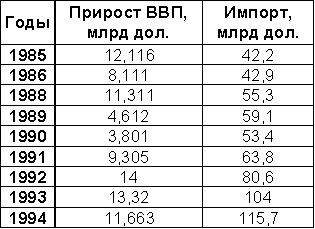
Некоторые исходные показатели экономического развития КНР (Источник: МЭ и международные отношения. – 2002. – № 8. – С. 65).
-
Исходные данные заработной платы от производительности труда.

-
Исходные данные товарооборота России и Японии в 1991 – 1995 гг. (Источник: Внешняя торговля. – 1995. – №2-3. – С. 21).

-
Исходные данные товарооборота России и Японии в 1991 – 1995 гг. (Источник: Внешняя торговля. – 1995. – №2-3. – С. 21).

-
Исходные данные притока прямых иностранных инвестиций в КНР (выбрать любую из пар зависимого и независимого показателей) (Источник: МЭ и международные отношения. – 2002. – № 8. – С. 66).
-
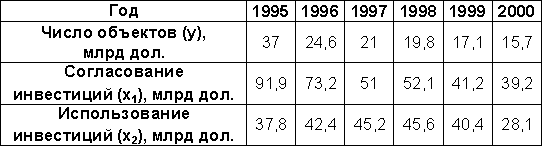
Исходные данные макроэкономических итогов политики за 6 лет (выбрать любую из пар зависимого и независимого показателей) (Источник: МЭ и международные отношения. – 2006. – № 2).
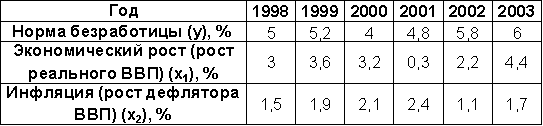
-
Исходные данные распределения добавленной стоимости по отраслям экономики в ЕС в 2002 г. (выбрать любую из пар зависимого и независимого показателей).

-
Исходные данные основных экономических показателей Армении в 1996 – 2002 гг. (выбрать любую из пар зависимого и независимого показателей) (Источник: Общество и экономика. – 2005. – № 4).
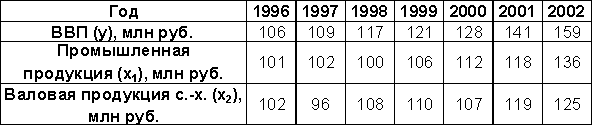
-
Исходные данные разнонаправленной динамики социально-экономического развития по группам наиболее и наименее развитых регионов России за 2004 г. (выбрать любую из пар зависимого и независимого показателей) (Источник: Экономист. – 2005. – №3).
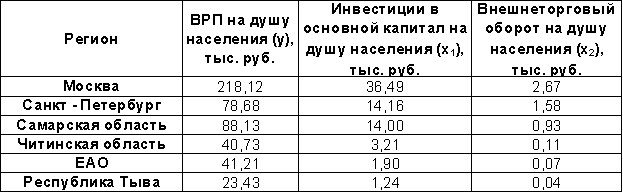
-
Исходные данные некоторых экономических показателей хозяйственно-финансовой деятельности с.-х. предприятий (выбрать любую из пар зависимого и независимого показателей) (Источник: Экономист. – 2005. – №3).
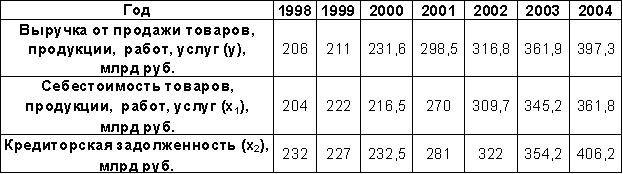
-
Исходные данные основных экономических показателей Украины в 1996 – 2002 гг. (выбрать любую из пар зависимого и независимого показателей) (Источник: Общество и экономика. – 2005. – № 4).
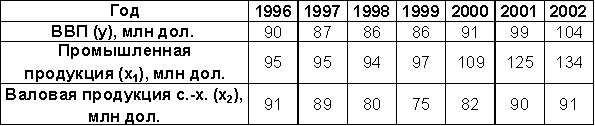
-
Исходные данные товарооборота России с Германией в 1992 – 1997 гг. (выбрать любую из пар зависимого и независимого показателей) (Источник: Внешняя торговля. – 1996. – №1-2. – С. 26).
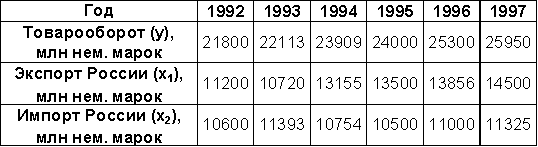
-
Исходные данные динамики основных показателей Китая с 1991 по 1996 гг. (выбрать любую из пар зависимого и независимого показателей).

-
Исходные данные товарооборота России и Кореи в 1991 – 1995 гг. (выбрать любую из пар зависимого и независимого показателей).

-
Исходные данные динамики основных показателей французской экономики за 6 лет (выбрать любую из пар зависимого и независимого показателей).

-
Исходные данные отраслевой структуры экономики США за 8 лет (выбрать любую из пар зависимого и независимого показателей).

Методические указания
Подбор параметров функции
-
Линейная функция
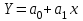
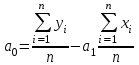 ,
, 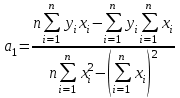
Коэффициент корреляции
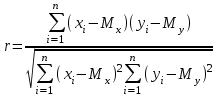
,
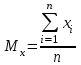 ,
, 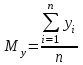
-
Квадратичная функция
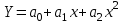
Система уравнений для определения коэффициентов функции.
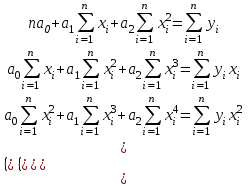
-
Кубическая функция
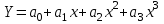
Система уравнений для определения коэффициентов функции.
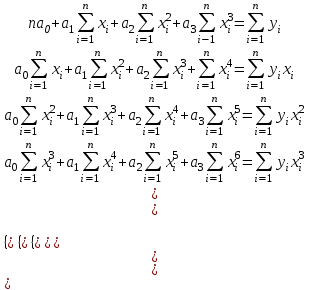
-
Показательная функция
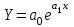
Для вычисления параметров функции необходимо выполнить некоторые арифметические преобразования, прологарифмируем функцию и получим:

Сделаем подстановку
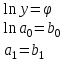
Функция приводится к линейной функции
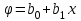
После нахождения коэффициентов b0 и b1 определим
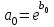
Индекс криволинейной корреляции определяется как