ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 17
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт финансов, экономики и управления
| (наименование института полностью) |
| Институт финансов, экономики и управления |
| (Наименование учебного структурного подразделения) |
| 38.03.01 Экономика |
| (код и наименование направления подготовки / специальности) |
| Финансы и кредит |
| (направленность (профиль) / специализация) |
Практические задания
по учебному курсу «Финансовые вычисления 1»
(наименование учебного курса)
Вариант ____ (при наличии)
| Обучающегося | А.С. Хрипко | |
| | (И.О. Фамилия) | |
| Группа | ЭКбд-1802а | |
| | | |
| Преподаватель | Морякова Анастасия Владимировна | |
| | (И.О. Фамилия) | |
Тольятти 2023
Бланк выполнения задания 1
Решение:
Для определения объема продукции х необходимо построить линейное уравнение, увязывающее в зависимость приведенные в условии задачи показатели. При этом:
выручка (
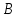
) представляет собой общий объем произведенной и реализованной продукции и определяется как произведение стоимости единицы продукции (
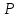) и общего объема произведенной продукции в натуральном выражении (
):
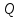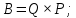
общая сумма затрат складывается из затрат постоянных и затрат переменных. Последние, в свою очередь, определяются как произведение суммы затрат, приходящейся на единицу произведенной продукции, и общего объема произведенной продукции в натуральном выражении:
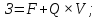
прибыль рассчитывается по формуле:
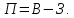
Записываем формулу:
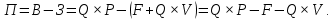
Из приведенной формулы выражаем объем производства:
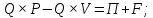
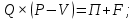
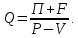
Осуществляем расчет:
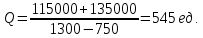
Вывод. Для получения прибыли в сумме 115 тыс. руб. предприятие должно произвести и реализовать 545 ед. продукции.
Бланк выполнения задания 2
Решение:
Осуществляем расчет себестоимости при разных объемах выпуска:
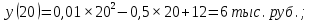
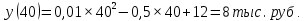
Записываем первую производную функции себестоимости:
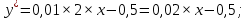
записываем вторую производную функции себестоимости:
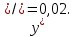
С помощью первой производной определяем скорость изменения себестоимости при разных объемах выпуска:
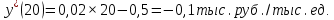
Полученное значение говорит о следующем: при указанном объеме увеличение объема выпуска на 1 тыс. ед. приводит к снижению себестоимости на 0,1 тыс. руб. Осуществляем проверку:
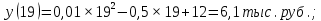
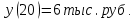
Таким образом, действительно, увеличение объема выпуска на 1 тыс. ед. дает снижение себестоимости с 6,1 до 6,0 тыс. руб., т.е. на 0,1 тыс. руб.
Аналогичные расчеты осуществляем из другого объема выпуска:
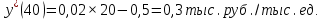
Осуществляем проверку:
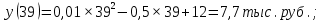
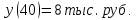
Да, действительно, в данном случае увеличение объема выпуска на 1 тыс. ед. дает, напротив, рост себестоимости с 7,7 до 8,0 тыс. руб., т.е. на 0,3 тыс. руб.
Темп изменения себестоимости, т.е. относительная скорость изменения себестоимости представляет собой логарифмическую производную функции себестоимости:
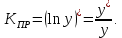
Осуществляем расчет:
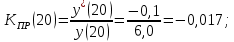
проверка:
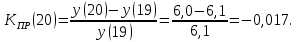
Таким образом, при объеме выпуска 20 тыс. ед. увеличение выпуска на 1% приводит к снижению себестоимости на 1,7%.
Продолжаем расчет:
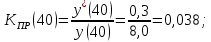
проверка:
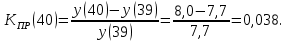
Таким образом, при объеме выпуска 40 тыс. ед. увеличение выпуска на 1% приводит к росту себестоимости на 3,8%.