Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и

Информатики
Межрегиональный центр переподготовки специалистов

Контрольная работа

По дисциплине: «Исследование операций»

Динамические игры с полной информацией
Выполнил: Мухин Е.Е.

Группа: ПИ-90

Вариант: 3


Проверил: Мейкшан В.И.

Новосибирск, 2021 г

Оглавление

Введение
В какой-либо конфликтной ситуации решение принимается не одним индивидуумом, а несколькими участниками, и функция выигрыша каждого индивидуума зависит не только от его стратегии, но также и от решений других участников. Математическая модель такого рода называется игрой, а участники конфликта игроками.

Если игроков двое, а интересы их противоположны, то игра называется антагонистической.

На практике участники конфликтов часто совершают свой выбор не один раз, а последовательно во времени, в зависимости от развития конфликта. Одним из классов игр, которые описывают конфликты, динамика которых влияет на поведение участников, являются позиционные игры.


1. Понятие динамической игры. Полная и неполная, совершенная и несовершенная информация. Дерево игры
Динамической называется игра, в которой каждый игрок может сделать несколько ходов, и, по крайней мере, один из игроков, делая ход, знает, какой ход сделал другой игрок (возможно, он сам).

Динамическая игра — более сложный объект, чем статическая игра. Для того, чтобы описать динамическое игровое взаимодействие нескольких субъектов, нам необходимо знать две вещи. Во-первых, это последовательность действий игроков при возможных сценариях развития событий в игре, а также выигрыши, получаемые игроками в зависимости от произошедших в игре событий. Во-вторых, необходимо знать, что каждому игроку может быть известно относительно ходов, уже сделанных другими игроками. В первом случае, мы говорим о дереве игры; во втором — об информационных множествах игроков¹.

В динамических играх различают полную и совершенную информацию.

Если все игроки имеют общую информацию о правилах игры и функциях выигрыша, то информацию считают полной. Это понятие в равной степени относится как к статическим, так и к динамическим играм.

Понятие совершенной информации относится только к динамическим играм, в которых игроки делают ходы последовательно в разные моменты времени. Говорят, что динамическая игра обладает совершенной информацией, если все сделанные ходы сразу же становятся известны всем игрокам².

Иногда динамическую игру удобно представить в виде дерева.

В данном случае, во-первых, нужно определить множество игроков. Для того, чтобы моделировать случайные события, влияющие на выигрыш игроков, необходимо определить еще одного игрока — природу.

Во-вторых, нужно определить, в каком порядке игроки ходят, и какие действия им доступны на каждом ходе³.

Представление в виде дерева называется развернутой формой игры. Она должна содержать⁴:

- множество вершин дерева игры, в том числе одну начальную вершину;

- для каждой вершины, кроме начальной – единственную вершину, которая непосредственно ей предшествует; при этом цепь предшествующих вершин, построенная из любой вершины, должна заканчиваться в начальной вершине (это предполагает отсутствие циклов);

- множество игроков;

- для каждой вершины, кроме конечных – единственного игрока, которому принадлежит ход в данной вершине;

- для каждой конечной вершины – вектор выигрышей всех игроков;

- (если в игре есть случайные ходы «природы», то следует задать также распределение вероятностей на множестве всех возможных ходов «природы»).

Пример. Игра «Террорист». В самолет сел террорист, который требует лететь из Майами в Гавану вместо Нью-Йорка. В предположении, что террорист не может определить маршрут полета, летчик выбирает, куда лететь. Если он летит в Гавану, игра заканчивается, а если в Нью-Йорк, то ход делает террорист, который решает, взрывать самолет или нет. На конечных вершинах дерева проставлены выигрыши игроков (первый игрок – пилот).



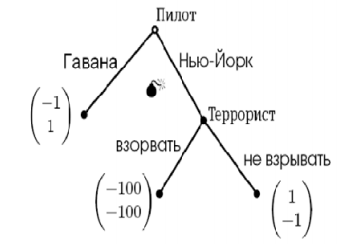
Рисунок 1. – Игра «Террорист»
Пример⁵: D игре «хулиган с гранатой» первый ход Прохожий; ему доступны действия «отдать» и «не отдавать». В случае, если выбрано действие «не отдать», делает ход Хулиган; его возможные действия — «взорвать» и «не взорвать». Эту информацию мы можем изобразить в виде следующего дерева (или графа) игры, изображенного на рис.


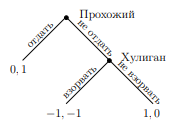
Рисунок 2. – Игра «Хулиган»
Дерево игры состоит из вершин и соединяющих их отрезков. Каждая вершина означает либо момент принятия решения одним из игроков, либо момент окончания игры. Моменты принятия решения обозначены жирными точками; их на нашем дереве два — принятие решения Прохожим, и принятие решения Хулиганом.

Всего существует три варианта окончания игры:

- если Прохожий отдает кошелек,

- если Прохожий не отдает кошелек и Хулиган взрывает гранату,

- если Прохожий не отдает кошелек, и Хулиган не взрывает.

В дереве игры всегда существует одна вершина, соответствующая началу игры. В нашем случае, это — вершина, в которой делает ход Прохожий.

Наконец, в-третьих, нам надо определить, как выигрыши игроков зависят от ходов, которые были сделаны. Формально, для каждой конечной вершины дерева игры мы определяем выигрыши для каждого игрока. В нашем случае, мы предполагаем, что выигрыш каждого игрока равен -1 в случае взрыва гранаты, 0 в случае, если взрыва нет, но игрок остался без кошелька, и 1, если взрыва не было, и кошелек остался у игрока.

Каждому ходу, который игрок делает в какой-то вершине, соответствует вершина, в которой игра оказывается после сделанного хода. Например, после хода Прохожего «отдать», игра переходит в конечную вершину с выигрышем (0, 1). После хода «не отдать» игра переходит в вершину, в которой ход делает Хулиган. Будем говорить, что вершина, в которой делает ход Прохожий, лежит выше, чем вершина, в которой делает ход Хулиган. В любом дереве игры, для любой вершины, кроме начальной, однозначно задается история игры — то есть последовательность вершин, через которые игра уже успела пройти. В частности, для любой вершины (опять же, кроме начальной) существует ровно одна вершина, непосредственно предшествующая данной. Это исключает «деревья» вроде графа, изображенного на рис. 3.



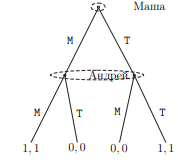
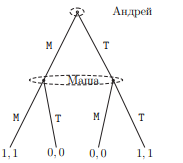
Рисунок 3, 4
Необходимость наличия начальной вершины исключает возможность циклов (рис.4).

2. Метод обратной индукции
В динамических играх с полной и совершенной информацией удобно решать игру методом обратной индукции.

В соответствии с методом обратной индукции игра «разматывается» с конца. При этом рассматриваются все последние вершины игры, в которых один из игроков делает выбор, исходя из его рациональности. Далее процесс повторяется для всех предшествующих вершин, пока не дойдет до начальной вершины⁶.

Например, в игре «Террорист» единственной вершиной, из которой можно начать применение метода обратной индукции («предфинальная» позиция), является вершина, в которой ход делает террорист. Террорист из двух вариантов (взрывать или не взрывать бомбу в Нью-Йорке) выбирает – не взрывать, поскольку при заданных выигрышах ему выгоднее именно не взрывать.

После этого игру можно частично свернуть (редуцировать), и дерево игры упрощается:



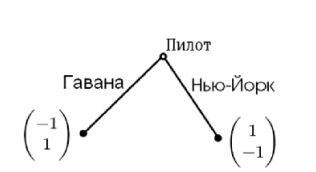
Рисунок 5
Поскольку действия террориста в Нью-Йорке несложно предугадать, пилот выбирает лететь в Нью-Йорк, где его выигрыш больше. Таким образом, обратная индукция показывает, что пилот полетит в Нью-Йорк, а террорист не будет взрывать бомбу. Обратную индукцию можно реализовать и на основе функций отклика игроков⁷.


3. Стратегия в динамической игре. Равновесия «пустых угроз». Совершенное в подыграх равновесие Нэша
Равновесие Нэша, совершенное по подыграм - концепция решения в теории игр, рафинирование равновесия Нэша для игр в развёрнутой форме. 

Набор стратегий игроков называется равновесием, совершенным по подыграм, если его сужение на любую подыгру данной игры есть равновесие Нэша в ней. Интуитивно это означает, что действия сторон в некоторой игре будут одинаковы, независимо от того, разыгрывается ли она отдельно или является частью более общей надыгры. 

Равновесие, совершенное по подыграм, позволяет отсеять равновесия Нэша, основанные на недостоверных угрозах игроков. 

Распространённый метод решения - обратная индукция, при которой оптимизация ходов игроков начинается с конца игры. Данный метод не работает, если в игре отсутствуют подыгры, а также для повторяющихся игр с бесконечным горизонтом.

Множество игроков и в нормальной форме, и в развернутой должно быть одним и тем же. Однако понятие стратегии в динамической игре требует уточнения.

Динамической называется игра, в которой каждый игрок может сделать несколько ходов, и по крайней мере один из игроков, делая ход, знает, какой ход сделал другой игрок (возможно, он сам).

В динамических играх различают полную и совершенную информацию. Если все игроки имеют общую информацию о правилах игры и функциях выигрыша, то информацию считают полной. Это понятие в равной степени относится как к статическим, так и к динамическим играм. Понятие совершенной информации относится только к динамическим играм, в которых игроки делают ходы последовательно в разные моменты времени. Говорят, что динамическая игра обладает совершенной информацией, если все сделанные ходы сразу же становятся известны всем игрокам.

Иногда динамическую игру удобно представить в виде дерева. Такое представление называется развернутой формой игры. Она должна содержать:

- множество вершин дерева игры, в том числе одну начальную вершину;

- для каждой вершины, кроме начальной – единственную вершину, которая непосредственно ей предшествует; при этом цепь предшествующих вершин, построенная из любой вершины, должна заканчиваться в начальной вершине (это предполагает отсутствие циклов);

- множество игроков;

- для каждой вершины, кроме конечных – единственного игрока, которому принадлежит ход в данной вершине;

- для каждой конечной вершины – вектор выигрышей всех игроков;

- (если в игре есть случайные ходы «природы», то следует задать также распределение вероятностей на множестве всех возможных ходов «природы»).

Пример. Игра «Террорист». В самолет сел террорист, который требует лететь из Майами в Гавану вместо Нью-Йорка. В предположении, что террорист не может определить маршрут полета, летчик выбирает,

куда лететь. Если он летит в Гавану, игра заканчивается, а если в Нью-Йорк, то ход делает террорист, который решает, взрывать самолет или нет. На конечных вершинах дерева проставлены выигрыши игроков (первый игрок – пилот): В динамических играх с полной и совершенной информацией удобно решать игру методом обратной индукции. В соответствии с методом обратной индукции игра «разматывается» с конца. При этом рассматриваются все последние вершины игры, в которых один из игроков делает выбор, исходя из его рациональности. Далее процесс повторяется для всех предшествующих вершин, пока не дойдет до начальной вершины. Например, в игре «Террорист» единственной вершиной, из которой можно начать применение метода обратной индукции («предфинальная» позиция), является вершина, в которой ход делает террорист. Террорист из двух вариантов (взрывать или не взрывать бомбу в Нью-Йорке) выбирает

– не взрывать, поскольку при заданных выигрышах ему выгоднее именно не взрывать.

Теорема. В игре с совершенной информацией и конечным числом ходов множество решений, получаемых обратной индукцией, совпадает с множеством СПРН.

Нормальная форма игры может быть очень громоздкой. Использование последней теоремы сильно упрощает поиск СПРН, поскольку не требует записи игры в нормальной форме и нахождения в ней РН⁸.

4. Модель дуополии Штакельберга

Дуополия (от латинского: два и греческого: продаю) — ситуация, при которой имеются только два продавца определённого товара, не связанных между собой монополистическим соглашением о ценах, рынках сбыта, квотах и др.

Модель асимметричной дуополии, предложенная Г. фон Штакельбергом в 1934 г., представляет развитие моделей количественной дуополии Курно и Чемберлина.

Асимметрия дуополии Штакельберга заключается в том, что дуополисты могут придерживаться разных типов поведения - стремиться быть лидером или оставаться последователем. Последователь Штакельберга придерживается предположений Курно, он следует своей кривой реагирования и принимает решения о прибылемаксимизирующем выпуске, полагая выпуск соперника заданным. Лидер Штакельберга, напротив, не столь наивен, как обыкновенный дуополистКурно, Он настолько изощрен в понимании рыночной ситуации, что не только знает кривую реагирования соперника, но и инкорпорирует ее в свою функцию прибыли⁹.

В отличие от модели Курно, в которой обе фирмы являются на рынке равноправными игроками, в модели Штакельберга одна из них (лидер I) активна, а другая (последователь II) пассивна. Последователь предоставляет лидеру возможность первому предложить на рынке желаемое количество товара и оставшийся после этого неудовлетворенный отраслевой спрос рассматривает как свою долю рынка.

Модель дуополии Курно представляет собой симметричную количественную дуополию, ибо обе фирмы придерживаются одного типа поведения на рынке. Первая (вторая) фирма полагает, что конкурирующая с ней вторая (первая) фирма имеет фиксированный выпуск в производственном периоде, т.е. она его не изменяет в этом периоде, если даже первая (вторая) фирма изменит свой выпуск, что

(1у ду2

йу2

*У

формально выражается так: —- = 0, —- = 0.

Модель дуополии Штакельберга — модель асимметричной количественной дуополии, ибо каждая из двух фирм придерживается одного из двух типов поведения: стремится стать либо лидером по объему выпускаемой продукции, либо последователем, т.е. следовать за лидером.

В этом параграфе проанализирована ситуация, когда одна фирма (например, первая) является лидером (по объему выпускаемой продукции), а другая фирма (вторая) является последователем.

Рассмотрим дуополию, когда издержки обеих фирм имеют соответственно вид С[ = су + (]ь С2 = су2 + (12, т.е. МС{ = МС2 = с.

Как и раньше, символом у{ обозначим объем выпуска первой фирмы (фирмы-лидера), символом у2 — объем выпуска второй фирмы (фирмы-последователя) в течение фиксированного периода. Символом у обозначена сумма у, + у2.

Согласно первой предпосылке Штакельберга вторая фирма полагает, что выпуск первой фирмы фиксирован в производственном периоде, т.е. не изменится в данном периоде, это формально означает следующее:

^ = 0, (5.23)

4у2

т.е. для второй фирмы сохраняется предпосылка Курно. Собственно, эта предпосылка делает вторую фирму фирмой-последователем.

Первая фирма, согласно второй предпосылке Штакельберга, предполагает, что вторая фирма сокращает в производственном периоде объем производства на 1/2, в соответствии с выражением (5.17), если первая фирма увеличивает объем своего производства на одну единицу, что формально означает, что

(5.24)

Собственно предпосылка (5.24) делает первую фирму фирмой-лидером. Прибыль РЯУ первой фирмы имеет вид РЯ{ = ру^ - су| - с1 -= (а-Ьу1-Ьу2)у1-су1-с11.

Для решения задачи максимизации прибыли ТУ?, первой фирмы следует сначала использовать условие первого порядка

с1РЯ

с1у

= а - с - 2Ьу - Ьу2 - Ьу^

(1у2

с!у{

(5.24)

= а - с -

-Ьу - Ьу2 = 0,

т.е. первая (фирма-лидер) учитывает в функции своей прибыли равенство (5.24).

Из последнего равенства получаем уравнение реакции первой фирмы ^^(уг) на выпуску второй фирмы:
2а - с 3 Ь
(5.25)

Прибыль РЯ2 второй фирмы имеет ВИД РЯ2 = ру2 - су2 - с12 = = (а - Ьу2- Ьу)у2- су2- с12.

Для решения задачи максимизации прибыли РЯ2 второй фирмы следует использовать условие первого порядка

дРЯ2 _, . . с/у,

ду.

с1у2

(5.23)

= а - с - 2Ьу2 - Ьу - 0,

= а -с- 2Ьу2 - Ьу - Ьу2 1 -

откуда получаем уравнение реакции второй фирмы на вы

пуск первой фирмы:

(5.26)

а-с у

У> ----С

2 2 Ь 2

Подставив выражение (5.25) в (5.26), получим
а-с

Ъ

2( а-с уЛ

2Ъ 2 у

откуда вытекает, что
а-с 2 Ъ

(5.27)

Подставив (5.27) в (5.26), получим



а-с



1 а-с

2 2Ь

а-с

4У'

---

Выпуски _у,(Л/|) и у 2*11 образуют равновесие Штакельберга 1, когда первая фирма является лидером, а вторая фирма является последователем. Если лидером является вторая фирма, а первая фирма является последователем, имеем равновесие Штакельберга 2.

Отметим, что в равновесии Штакельберга 1 объем выпуска первой фирмы в два раза больше объема выпуска второй фирмы.

Сведем все характеристики равновесий 1 и 2 по Штакельбергу в табл. 5.1, в которую также поместим все характеристики равновесия Курно

Уравнение изопрофиты первой фирмы (фирмы-лидера), соответствующей ее максимальной прибыли РЯ, имеет вид

(а - с)ух - Ьу1 - Ьуху2 -с!х= С) - (5.28)

8 о

откуда следует, что

а-с
Ъ

1 (а-с)2 1

8 Ь2 V

(5.29)
Такое взаимоотношение между конкурентами может возникнуть вследствие ассиметричного распределения информации: лидер знает функцию затрат последователя, в то время как последователь не осведомлен о производственных возможностях лидера.

В такой ситуации фирмам не нужно принимать стратегических решений. Прибыль лидера зависит только от его объема выпуска, так как объем выпуска последователя задан уравнением его реакции: qII = qII(qI).

Для наглядного сопоставления равновесия Курно с равновесием Штакельберга линии реакции дуополистов нужно дополнить линиями равной прибыли (изопрофитами). Уравнение изопрофиты получается в результате решения уравнения прибыли дуополии относительно объема выпуска, обеспечивающего заданную величину прибыли.


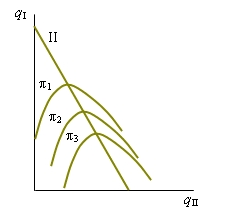
Рисунок 6 – Изопрофиты дуополии
На рисунке 6 показано, как располагаются изопрофиты фирмы II. При заданном выпуске фирмы I соответствующая ему точка на линии реакции фирмы II указывает объем ее производства, максимизирующий прибыль. Получить такую же прибыль при большем или меньшем своем выпуске фирма II может только, если фирма I уменьшит предложение на рынке, поэтому вершины изопрофит располагаются на линии реакции. Чем ниже расположена изопрофита, тем большую прибыль она представляет, так как соответствует меньшему выпуску конкурента.

Совместив карты изопрофитдуополистов, можно увидеть сочетания q_I,q_II, соответствующие отраслевому равновесию в моделях Курно и Штакельберга (рис. 7). Точка пересечения линий реакции (С) представляет равновесие в модели Курно, а точка касания линии реакции последователя с наиболее низкой изопрофитой лидера представляет равновесие в модели Штакельберга (

---

S_I или S_II).


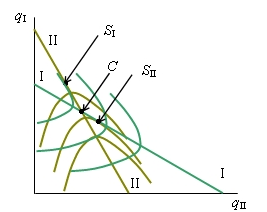
Рисунок 7. - Равновесный выпуск в моделях Курно и Штакельберга
Из рисунке 7 следует, что у фирмы, становящейся лидером, прибыль увеличивается по сравнению с той, которую она получала при конкуренции по модели Курно: лидер переходит на более низкую изопрофиту.

Можно доказать, что при линейных функциях отраслевого спроса и общих затрат дуополистов в модели Штакельберга рыночная цена будет ниже, чем в модели Курно⁹.

Картель. Поскольку максимальную прибыль на рынке гомогенного блага обеспечивает монопольная цена, то наибольшую прибыль дуополисты (олигополисты) получат в случае организации картеля - явного или тайного сговора об ограничении рыночного предложения с целью поддержания монопольной цены.

Однако картельное соглашение не является равновесием Нэша, так как каждый участник картеля может повысить прибыль за счет увеличения своего выпуска, пока другие придерживаются соглашения. Вероятность нарушения картельного соглашения возрастает по мере увеличения числа его членов¹⁰.

5. Модель Рубинштейна
Рубинштейн дал критическую интерпретацию требованию рациональности, анализируя концепцию «совершенногоравновесия». Длятогочтобыравновесиебылосовершенным, недостаточно, чтобы пара выбранных в начале игры стратегий была лучшей для каждого игрока в том смысле, что при заданном выборе оппонента у него не существует никакой другой стратегии, которая бы приводила к более выгодному исходу. Планируемые стратегии также должны формировать равновесие в каждом раунде игры при всех возможных вариантах предыстории (в противном случае предложение любого эффективного по Парето распределения и его одобрение может быть равновесным).

В частности, в любой точке договорного процесса, рассматриваемого в виде чередующейся последовательности предложений и отказов, должны быть выполнены следующие условия:

1) игрок, чья очередь делать предложение, не имеет альтернативы лучше той, что предписана ему стратегией;

2) другой игрок, планируя принять (отвергнуть) предложение в определенный момент времени, не может улучшить своего положения, отказавшись от (приняв) него.

В модели Рубинштейна риск разрыва сотрудничества является в большей мере экзогенным, а не возникает в результате принятия игроками решения прекратить кооперацию. Например, фирма и профсоюз предприятия договариваются о распределении квазиренты, которое можно осуществить только после достижения соответствующего соглашения. Однако в определенный момент времени возможность получения квазиренты может быть перехвачена конкурирующей фирмой, и вероятность этого события является постоянным во времени параметром. Другая интерпретация его модели заключается в том, что

---

исходный и представляют собой выигрыши, обеспечивающие статус-кво участников. Если обе стороны достигают согласия, то возможность получения квазиренты возрастает. Однако они должны постоянно индексировать (дисконтировать) размер своих будущих выигрышей с учетом временного коэффициента дисконтирования. Другими словами, они заинтересованы в скорейшем достижении согласия¹¹.

Заключение
В конце работы, можно сделать выводы.

Динамическая игра — модель, предполагающая возможность сделать несколько ходов каждому из игроков в процессе игры и возможность корректировки стратегий каждого из игроков с учетом уже сделанных ходов всех игроков.

Динамические игры — игры, в которых игроки принимают решения в зависимости от уже сделанных ходов других игроков.

Динамические игры с полной информацией — игры, для которых выполняется принцип общего знания: все игроки обладают одинаковой информацией об уже сделанных и возможных ходах всех других игроков и эта информация является общим знанием.

В динамических играх, как и в с статических, игроки должны выбирать свои стратегии при предположении возможных ходов всех других игроков.

Одним из вариантов динамической игры является иерархическая игра, т. е. игра в которой один игрок (центр) имеет право первого хода, а другие игроки (агенты) выбирают свои стратегии, ориентируясь на стратегию центра. Задача центра — выбрать такую стратегию, которая максимизировала бы его платеж вместе со стратегиями, выбранными агентами в овеет на стратегию центра.

Можно привести много примеров сложных информационных взаимодействий в различных системах - экономических, социальных, политических, технических, биологических. Последние, например, подробно обсуждаются в [1]. Информационное взаимодействие в системах может описываться разными математическими средствами и, в частности, такими, как стохастические динамические игры с равновесием по Нэшу. Выбор игроком на каждом шаге игры управляющего решения основан, прежде всего, на информации, доступной ему на тот момент. Характер и объем этой информации для каждого из участников игры называется информационной структурой игры.


Список использованных источников

1. 
   Захаров А.В. Теория игр в общественных науках, 2010 [Электронный ресурс] URL: http://iamdrunk.ru/teach/учеба_пгати/2010-2011/1%20семестр/Теория%20Информационных%20Процессов%20и%20Систем/game_theory.pdf
   
2. 
   Зенкевич Н.А., Петросян Л.А., Янг Д.В.К. Динамические игры и их приложения в менеджменте: учеб. пособие / Н.А.Зенкевич, Л.А. Петросян, Д.В.К. Янг; Высшая школа менеджмента СПбГУ. — СПб.: Изд-во «Высшая школа менеджмента», 2009.— 415 с.
   
3. 
   Конюховский, П. В. Теория игр : учебник для академического бакалавриата / П. В. Конюховский, А. С. Малова. — М. : Издательство Юрайт, 2015. — 252 с.
   
4. 
   Модели Рубинштейна [Электронный ресурс] URL: http://www.soldiers-mothers-rus.ru/stati/modeli-rubinshteina55
   
5. 
   Модель дуополии Штакельберга [Электронный ресурс] URL: http://www.economicus.ru/site/grebenikov/E_Micro/chap6/6_2/6_2_1_1.html
   
6. 
   МОДЕЛЬ ШТАКЕЛЬБЕРГА [Электронный ресуру] URL: https://uchebnik-ekonomika.com/uchebnik_mikroekonomika/11213-model-shtakelberga-22190.html
   
7. 
   Печерский Л.С. , Беляева А.А. Теория игр для экономистов. Вводный курс [Электронный ресурс] URL: http://www.allmath.ru/appliedmath/operations/operations22/operations.htm
   
8. 
   Шагин, В. Л. Теория игр : учебник и практикум для академического бакалавриата / В. Л. Шагин. — М. : Издательство Юрайт, 2015. — 223 с
   
9. 
   Челноков, А. Ю. Теория игр : учебник и практикум для бакалавриата и магистратуры / А. Ю. Челноков. — М. : Издательство Юрайт, 2016. — 223 с
   
10. 
    Черемных Ю.Н.. Микроэкономика. Продвинутый уровень: Учебник. - М.: ИНФРА-М, - 844 с.. 2008
    

---

---

Смотрите также файлы

• Реферат Средства управления процессами в ос windows Содержание I. Операционная система как система управления ресурсами и процессами 2 II. Управление процессами в ос windows 6 iii. Диспетчер задач 9.doc

• Хозяйственная операция.doc

• 2й вариант Отличие делового общения от обыденного.docx

• "Сенімен Болаша" Тркістан облысты Жастар анатыны ісшаралар жоспары.docx

• Пэ как одна из отраслей научного знания, выполняет.doc