МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Ижевский государственный технический университет имени М. Т. Калашникова»

Кафедра АСОИУ

ОТЧЁТ

по практической работе № 2

по дисциплине «Основы системного анализа»

на тему «Принятие решений в условия риска и неопределенности»


Выполнил

студент гр. Б20-782-1зу С. А. Насонова
Проверил

канд. физ.-мат. наук, доцент кафедры АСОИУ Е. В. Касаткина

Ижевск 2023

Постановка задачи

Возможно строительство 8 электростанций. Эффективность каждого из типов зависит от различных факторов. Предполагается, что выделено 6 различных состояний, каждое из которых означает определенное сочетание влияющих на эффективность объектов факторов. Экономическая эффективность отдельных типов электростанций задана матрицей А (см. исходные данные). Строки соответствуют различным альтернативам, столбцы – состояниям среды.

Задание

1. 
   Принять решение о строительстве электростанции с использованием классических критериев:
   

1. 
   критерий Вальда;
   
2. 
   критерий азартного игрока;
   
3. 
   критерий Гурвица (установить диапазоны принятия различных альтернатив при λϵ[0; 1]);
   
4. 
   критерий Лапласа;
   

2. 
   Принять решение о строительстве электростанции с использованием критериев с сожалениями:
   

1. 
   критерий Сэвиджа;
   
2. 
   критерий Лапласа с сожалениями;
   
3. 
   критерий субъективно-средних сожалений;
   

3. 
   Принять решение о строительстве электростанции при учете заданных вероятностей с использованием критериев:
   

1. 
   критерий максимальной вероятности;
   
2. 
   критерий Байеса;
   
3. 
   критерий Ходжа-Лемана (установить диапазоны принятия различных альтернатив при μϵ[0; 1]);
   
4. 
   критерий минимума дисперсии оценочного функционала.
   

4. 
   Провести анализ чувствительности принятого на основе критерия Байеса решения (рассмотреть не менее 10 наборов вероятностей).
   
5. 
   Найти Парето оптимальные решения и принять решение с использованием правила одновременного учета среднего ожидаемого дохода и среднего ожидаемого риска, понимаемого как стандартное отклонение (4*M(Fi) – 3*σ(Fi)).
   
6. 
   Провести исследование решения, полученного по критерию Байеса в случае обращения в консалтинг. Базируясь на байесовском подходе, а также учитывая статистическую информацию о деятельности консалтинговой фирмы, сделать вывод об оценке стоимости консалтинговых услуг, при которой обращение в эту фирму окажется выгодным для ЛПР. Нарисовать полное дерево решений для обоснования полученных выводов при обращении в консалтинг.
   

---

Вариант 13

A1	53	91	129	130	108	50
A2	37	37	54	60	141	86
A3	105	138	28	71	43	-3
A4	67	138	47	33	15	130
A5	64	-5	16	146	123	83
A6	29	14	-6	-2	76	75
A7	-8	46	41	46	38	107
A8	101	81	23	150	84	15
pi	0.1	0.09	0.22	0.22	0.3	0.007

Статистические данные о надежности прогнозов имеют следующий вид (Условные вероятности правильности прогноза):

Реальные состояния	Прогноз
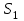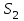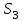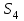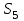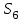S1	0,6	0,3	0,05	0,02	0,02	0,01
S2	0,15	0,6	0,15	0,05	0,025	0,025
S3	0,05	0,2	0,6	0,1	0,025	0,025
S4	0,05	0,05	0,15	0,6	0,1	0,05
S5	0	0,025	0,025	0,2	0,6	0,15
S6	0	0	0,05	0,1	0,25	0,6

---

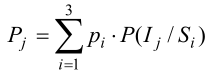
Полные вероятности:



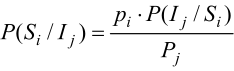
Апостериорные вероятности:
Для определения наиболее предпочтительного типа электростанции можно умножить каждый элемент матрицы А на соответствующий элемент вектора pj, а затем сложить результаты для каждого типа электростанции.

Например, для расчета эффективности первого типа электростанции можно выполнить следующую операцию:

A1: (53*0.1) + (91*0.09) + (129*0.22) + (130*0.22) + (108*0.3) + (50*0.07) = 106.37

Аналогичные операции можно выполнить для всех типов электростанций и выбрать тот, у которого результат будет наибольшим.

Таким образом, для принятия решения о выборе типа электростанции нужно выполнить математическое моделирование, учитывающее данные матрицы А и вектора pj.

A2: (37*0.1) + (37*0.09) + (54*0.22) + (60*0.22) + (141*0.3) + (86*0.07) = 80.43

A3: (105*0.1) + (138*0.09) + (28*0.22) + (71*0.22) + (43*0.3) + (-3*0.07) = 57.39

A4: (67*0.1) + (138*0.09) + (47*0.22) + (33*0.22) + (15*0.3) + (130*0.07) = 50.32

A5: (64*0.1) + (-5*0.09) + (16*0.22) + (146*0.22) + (123*0.3) + (83*0.07) = 84.3

A6: (29*0.1) + (14*0.09) + (-6*0.22) + (-2*0.22) + (76*0.3) + (75*0.07) = 30.45

A7: (-8*0.1) + (46*0.09) + (41*0.22) + (46*0.22) + (38*0.3) + (107*0.07) = 41.37

A8: (101*0.1) + (81*0.09) + (23*0.22) + (150*0.22) + (84*0.3) + (15*0.07) = 81.7

Наибольшим значением эффективности будет A1 = 106.37

1. 
   Принять решение о строительстве электростанции с использованием классических критериев:
   

1. 
   критерий Вальда
   

Строим матрицу:

Ai	П1	П2	П3	П4	П5	П6	min(A)
A1	53	91	129	130	108	50	50
A2	37	37	54	60	141	86	37
A3	105	138	28	71	43	-3	-3
A4	67	138	47	33	15	130	15
A5	64	-5	16	146	123	83	-5
A6	29	14	-6	-2	76	75	-6
A7	-8	46	41	46	38	107	-8
A8	101	81	23	150	84	15	15

---

Критерий Вальда для выбора типа электростанции определяется как наименьший элемент в каждой матрице А по строкам. Таким образом, для каждого состояния выбирается тип станции, который имеет наибольший минимальный элемент в соответствующей строке матрицы А:

Выбираем из(50; 37; -3; 15; -5; -6; -8; 15)

min=-8

Вывод: тип электростанции с наименьшим минимальным значением – A7, соответствует наибольшей осторожности и выбирается на основе критерия Вальда.

2. 
   критерий азартного игрока
   

Для критерия азартного игрока, выбирается альтернатива с максимальным значением максимума из всех возможных значений для каждой альтернативы и каждого состояния среды.

Вариант 13

Ai	П1	П2	П3	П4	П5	П6	max(A)
A1	53	91	129	130	108	50	130
A2	37	37	54	60	141	86	141
A3	105	138	28	71	43	-3	138
A4	67	138	47	33	15	130	138
A5	64	-5	16	146	123	83	146
A6	29	14	-6	-2	76	75	76
A7	-8	46	41	46	38	107	107
A8	101	81	23	150	84	15	150

---

Принятие решения:

Теперь выберем альтернативу с максимальным значением максимума из всех возможных значений. Исходя из расчетов, альтернатива с максимальным значением максимума имеет значение 150 и соответствует альтернативе A8.

Вывод: на основе критерия азартного игрока, рекомендуется выбрать альтернативу A8 - строительство электростанции.

3. 
   Критерий Гурвица
   

Для критерия Гурвица с параметром λ, необходимо найти максимум из взвешенных значений максимумов и минимумов для каждой альтернативы и каждого состояния среды. В данном случае, так как у нас задан диапазон значений параметра λ ∈ [0; 1], мы можем выбрать различные значения λ в этом диапазоне и оценить результаты.

Произведём расчет для λ = 0.5

A1 = λ * max(53, 91, 129,130, 108, 50) + (1 - λ) * min(53, 91, 129,130, 108, 50) = 0.5 * 130 + 0.5 * 50 = 90

A2 = λ * max(37, 37, 54, 60, 141, 86) + (1 - λ) * min(37, 37, 54, 60, 141, 86) = 0.5 * 141+ 0.5 * 37= 89

A3 = λ * max(105, 138, 28, 71, 43, -3) + (1 - λ) * min(105, 138, 28, 71, 43, -3) = 0.5 * 138 + 0.5 * -3 = 67.5

A4 = λ * max(67, 138, 47, 33, 15, 130) + (1 - λ) * min(67, 138, 47, 33, 15, 130) = 0.5 * 138 + 0.5 * 15 = 76.5

A5 = λ * max(64, -5, 16, 146, 123, 83) + (1 - λ) * min(64, -5, 16, 146, 123, 83) = 0.5 * 146+ 0.5 * -5 = 70.5

A6 = λ * max(29, 14, -6, -2, 76, 75) + (1 - λ) * min(29, 14, -6, -2, 76, 75) = 0.5 * 76 + 0.5 * -6 = 35

A7 = λ * max(-8, 46, 41, 46, 38, 107) + (1 - λ) * min(-8, 46, 41, 46, 38, 107) = 0.5 * 107 + 0.5 * -8 = 49.5

A8 = λ * max(101, 81, 23, 150, 84, 15) + (1 - λ) * min(101, 81, 23, 150, 84, 15) = 0.5 * 150 + 0.5 * 15 = 82.5

Таким образом, для параметра λ = 0.5, значения критерия Гурвица для всех альтернатив будут следующими:

max=90

Вывод: выбираем стратегию A1.

Определение диапазона принятия альтернатив

Диапазон принятия альтернатив можно определить, выбрав значения параметра λ в диапазоне [0; 1] и сравнив значения критерия Гурвица для каждой альтернативы. В данном случае, более высокие значения критерия Гурвица соответствуют более предпочтительным альтернативам.

Например, если мы выберем λ = 0.7, то значения критерия Гурвица будут следующими:

A1 = 0.7 * 130 + 0.3 * 50 = 106

A2 = 0.7 * 141 + 0.3 * 37 = 109.8

A3 = 0.7 * 138 + 0.3 * -3 = 95.7

A4 = 0.7 * 138 + 0.3 * 15 = 101.1

A5 = 0.7 * 146 + 0.3 * -5 = 100.7

A6 = 0.7 * 76 + 0.3 * -6= 51.4

A7 = 0.7 * 107 + 0.3 * -8 = 72.5

A8 = 0.7 * 150 + 0.3 * 15 = 109.5

Вывод: при λ = 0.7, наиболее предпочтительной альтернативой будет А2, так как она имеет наивысшее значения критерия Гурвица.

4. 
   Критерий Лапласа
   

Найдем математическое ожидание (среднее значение) для каждой альтернативы путем вычисления суммы значений в каждом столбце и деления на количество состояний среды:

Математическое ожидание (среднее значение):

---

Смотрите также файлы

• Выполнение задания позволяет сформировать.docx

• Задания суммативного оценивания за 4 четверть.docx

• Практическая работа 1. Задание 1.docx

• Организация Договора о коллективной безопасности.docx

• 1. Пестициды.pdf