Файл: Тесты по дисциплине Надежность и ремонт с х. техники.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 279
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 – Р(А) = 0
2 – Р(А) > 0
3 – Р(А) < 1
4 – Р(А) > 1
5 – Р(А) = 1
152. Как называется величина, которая в результате испытания (опыта) может принимать различные значения в определенных пределах? Какая это величина?
1 – постоянная
2 – переменная
3 – непрерывная
4 – дискретная
5 – случайная
153. Какие существуют два вида случайных величин? Какие бывают случайные величины?
1 – постоянные и переменные
2 – непрерывные и дискретные
3 – зависимые и независимые
4 – дифференциальные и интегральные
5 – целые и дробные
154. Как называется случайная величина, которая в некотором интервале может принимать любое значение? Какая это случайная величина?
1 – постоянная
2 – переменная
3 – непрерывная
4 – дискретная
5 – случайная
155. Как называется случайная величина, которая в некотором интервале может принимать только определенные значения, которые можно заранее перечислить? Какая это случайная величина?
1 – постоянная
2 – переменная
3 – непрерывная
4 – дискретная
5 – случайная
156. Как называется всякое соотношение, устанавливающее связь между возможными значениями случайных величин и соответствующими этим значениям вероятностями или частотами (часностями)? Что это?
1 – закон распределения случайной величины
2 – доверительный интервал
3 – выборка
4 – генеральная совокупность
5 – случайная зависимость
157. Как называется представление случайной величины в виде таблицы, в которой в одной строке представлены отсортированные в порядке возрастания значения случайной величины, а в другой строке – соответствующие этим значениям вероятности? Что это?
1 – отсортированная последовательность
2 – выборка
3 – ряд распределения
4 – дифференциальная функция распределения
5 – интегральная функция распределения
158. Как называется представление случайной величины в виде графика, где по оси абсцисс отложены значения случайной величины, а по оси ординат – соответствующие этим значениям вероятности и полученные точки соединены ломаной линией? Что это?
1 – полигон
2 – многоугольник распределения
3 – ряд распределения
4 – дифференциальная функция распределения
5 – интегральная функция распределения
159. Как называется число одинаковых или близких (полученных по наблюдениям) появлений события или абсолютных значений случайных величин, соединенных в одну группу (интервал) или разряд? Что это?
1 – выборка
2 – опытная вероятность
3 – частота
4 – частность
5 – математическое ожидание
160. Как называется частота, выраженная в долях единицы или процентах от общего числа испытаний или объектов изучаемой совокупности? Что это?
1 – выборка
2 – частность или опытная вероятность
3 – удельная частота
4 – среднее значение
5 – математическое ожидание
161. Как называется функция, записываемая следующим выражением: F(t) = P(T < t)?
1 – нормального распределения
2 – функция закона экспоненциального распределения
3 – функция закона распределения Вейбулла
4 – интегральная функция распределения
5 – дифференциальная функция распределения
162. Чему равно это выражение: dF(x)/dx = ?
1 – F(x)
2 – f(x)
3 – 1
4 –
5 – v
163. Чему равно это выражение:
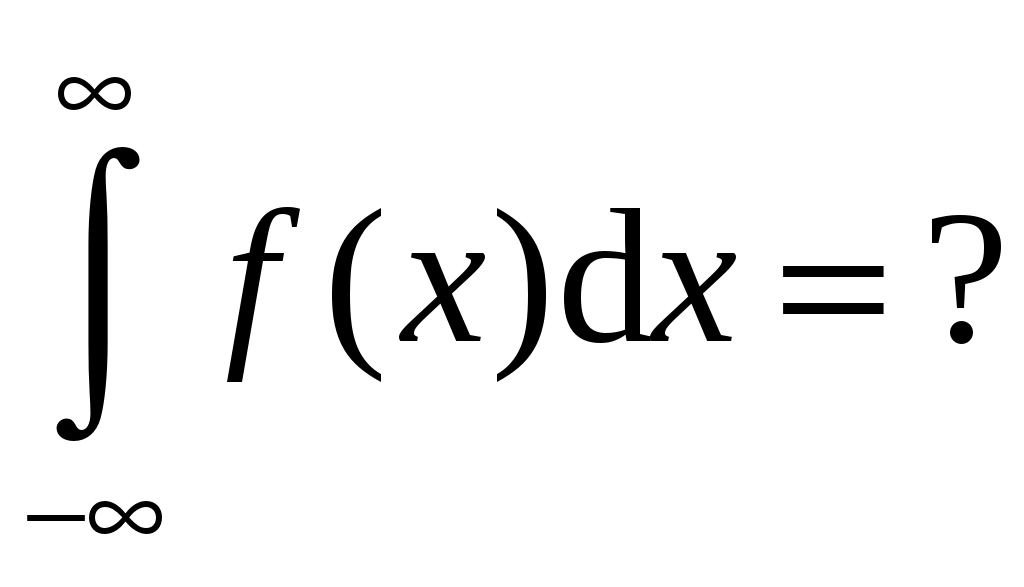
1 – F(x)
2 – f(x)
3 – 1
4 –
5 – v
164. Чему равно это выражение:
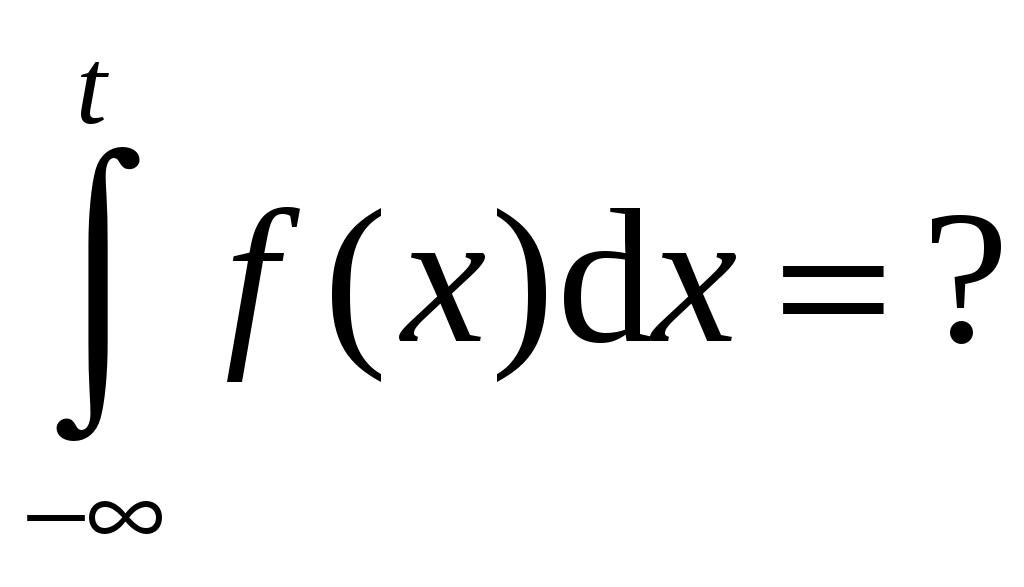
1 – F(x)
2 – f(x)
3 – 1
4 –
5 – v
165. Чему равно это выражение:
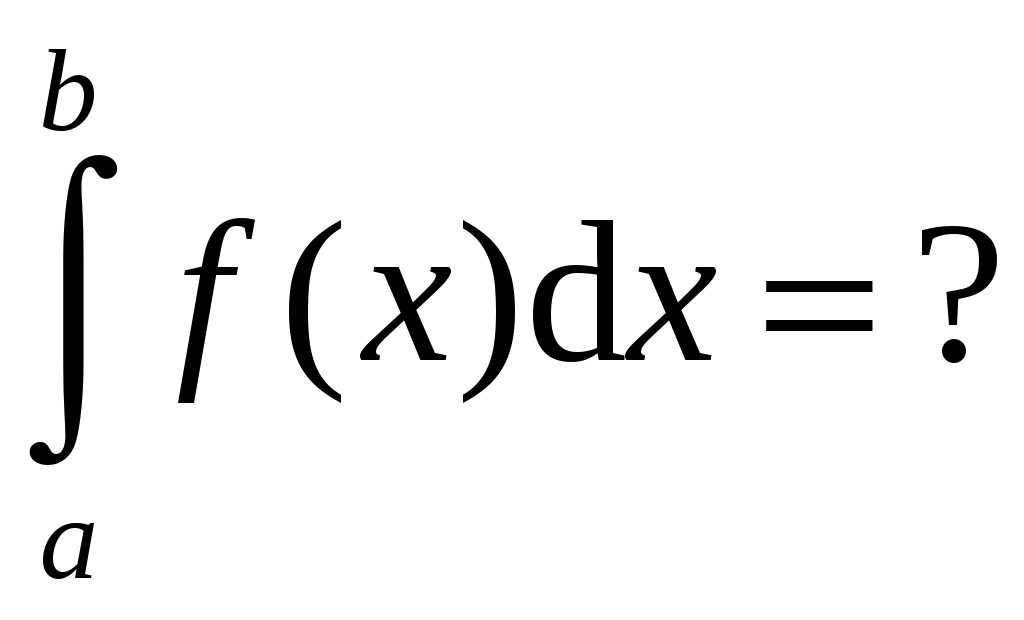
1 – F(x)
2 – D(x)
3 – F(a) - F(b)
4 –
5 – v
166. Чему равно это выражение:
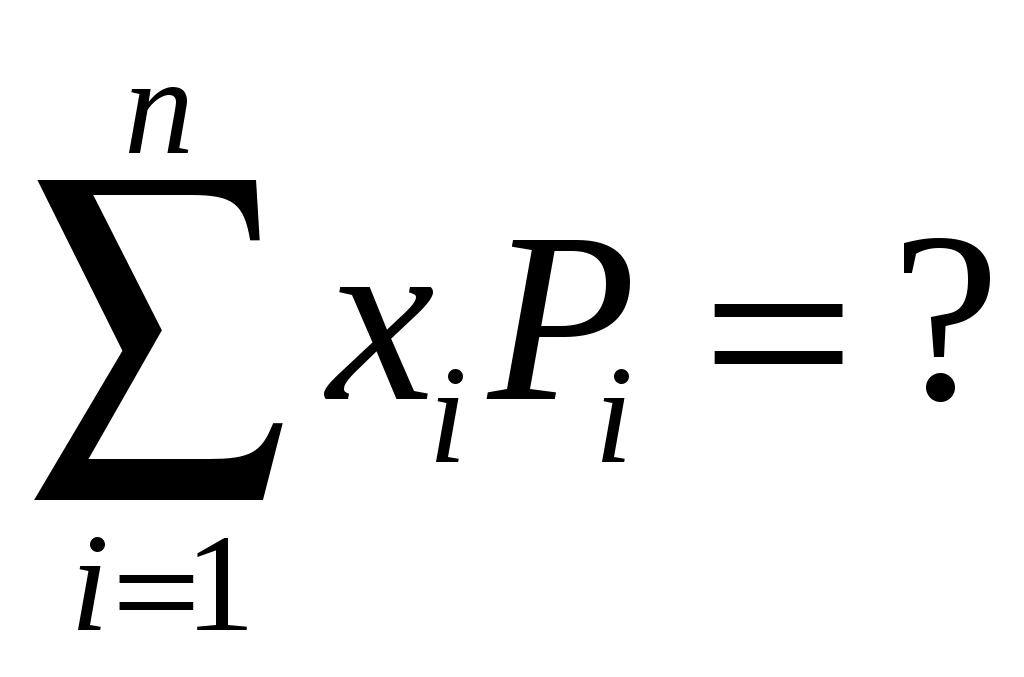
1 – F(x)
2 – D(x)
3 – M(x)
4 –
5 – v
167. Чему равно это выражение:
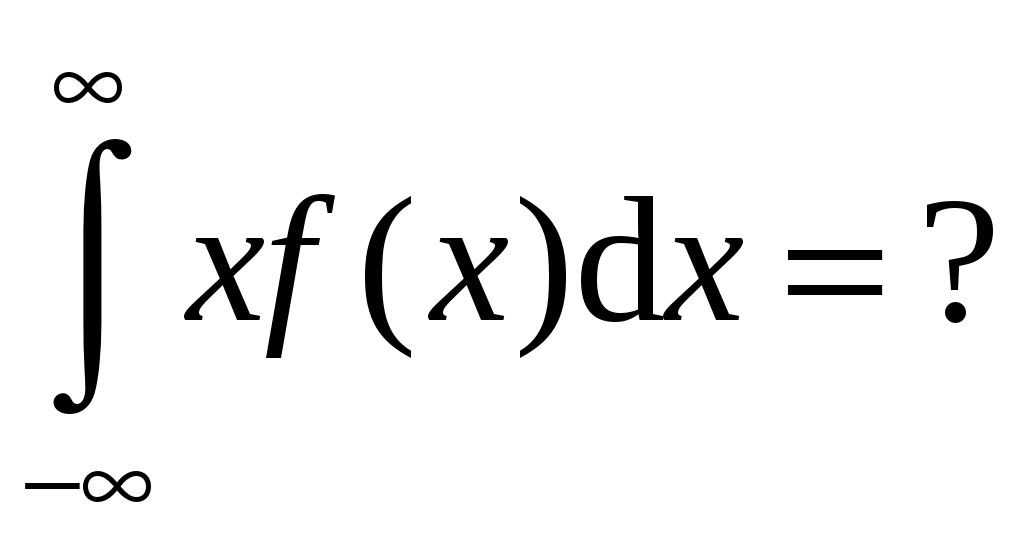
1 – F(x)
2 – D(x)
3 – M(x)
4 –
5 – v
168. Чему равно это выражение:
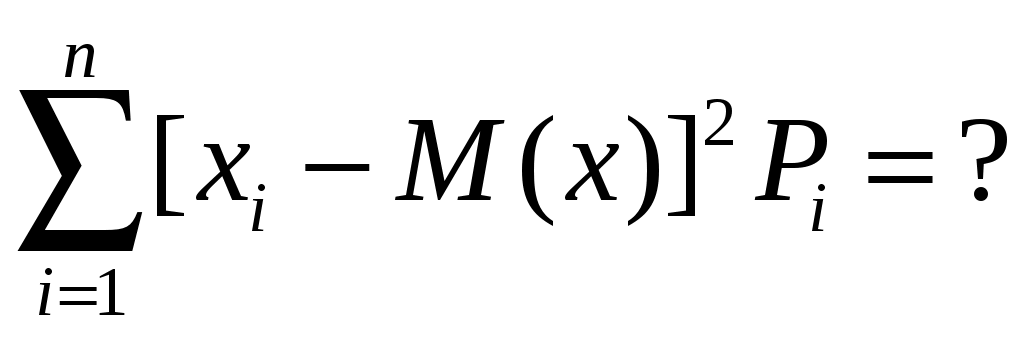
1 – F(x)
2 – D(x)
3 – M(x)
4 –
5 – v
169. Чему равно это выражение:
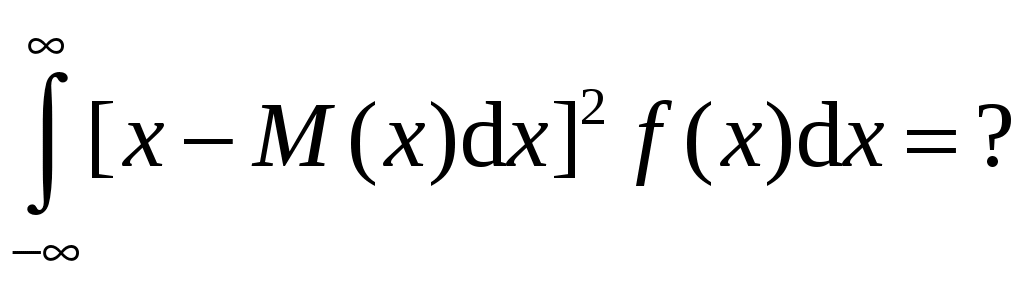
1 – F(x)
2 – D(x)
3 – M(x)
4 –
5 – v
170. Чему равно это выражение:
1 – F(x)
2 – D(x)
3 – M(x)
4 –
5 – v
171. Чему равно это выражение: (X)/M(X) = ?
1 – F(x)
2 – D(x)
3 – M(x)
4 –
5 – v
172. Что рассчитывается по этой формуле: dF(x)/dx = ?
1 – интегральная функция распределения непрерывной случайной величины
2 – интегральная функция распределения дискретной случайной величины
3 – математическое ожидание непрерывной случайной величины
4 – функция плотности распределения дискретной случайной величины
5 – функция плотности распределения непрерывной случайной величины
173. Что рассчитывается по этой формуле:

1 – интегральная функция распределения непрерывной случайной величины
2 – интегральная функция распределения дискретной случайной величины
3 – математическое ожидание непрерывной случайной величины
4 – функция плотности распределения дискретной случайной величины
5 – функция плотности распределения непрерывной случайной величины
174. Что рассчитывается по этой формуле:

1 – интегральная функция распределения непрерывной случайной величины
2 – интегральная функция распределения дискретной случайной величины
3 – математическое ожидание непрерывной случайной величины
4 – дисперсия дискретной случайной величины
5 – дисперсия непрерывной случайной величины
175. Что рассчитывается по этой формуле:

1 – интегральная функция распределения непрерывной случайной величины
2 – интегральная функция распределения дискретной случайной величины
3 – математическое ожидание непрерывной случайной величины
4 – дисперсия дискретной случайной величины
5 – дисперсия непрерывной случайной величины
176. Что рассчитывается по этой формуле:

1 – интегральная функция распределения непрерывной случайной величины
2 – математическое ожидание дискретной случайной величины
3 – математическое ожидание непрерывной случайной величины
4 – дисперсия дискретной случайной величины
5 – дисперсия непрерывной случайной величины
177. Что рассчитывается по этой формуле:

1 – интегральная функция распределения непрерывной случайной величины
2 – математическое ожидание дискретной случайной величины
3 – математическое ожидание непрерывной случайной величины
4 – дисперсия дискретной случайной величины
5 – дисперсия непрерывной случайной величины
178. Что рассчитывается по этой формуле:

1 – интегральная функция распределения непрерывной случайной величины
2 – вероятность попадания случайной величины в заданный интервал
3 – математическое ожидание непрерывной случайной величины
4 – среднее квадратическое отклонение
5 – коэффициент вариации
179. Что рассчитывается по этой формуле:
1 – интегральная функция распределения непрерывной случайной величины
2 – вероятность попадания случайной величины в заданный интервал
3 – математическое ожидание непрерывной случайной величины
4 – среднее квадратическое отклонение
5 – коэффициент вариации
180. Что рассчитывается по этой формуле: (X)/M(X) = ?
1 – интегральная функция распределения непрерывной случайной величины
2 – вероятность попадания случайной величины в заданный интервал
3 – математическое ожидание непрерывной случайной величины
4 – среднее квадратическое отклонение
5 – коэффициент вариации
181. Что является важнейшим показателем качества машины?
1 – внешний вид
2 – удобство управления
3 – надежность
4 – сопротивление передвижению
5 – коррозионная стойкость
182. Как называется свойство объекта сохранять во времени и в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования? Что это?
1 – надежность
2 – безотказность
3 – долговечность
4 – ремонтопригодность
5 – сохраняемость
183. Как называется свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки? Что это?
1 – надежность
2 – безотказность
3 – долговечность
4 – ремонтопригодность
5 – сохраняемость
184. Как называется свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений и поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонтов? Что это?
1 – надежность
2 – безотказность
3 – долговечность
4 – ремонтопригодность
5 – сохраняемость