Лекция 6.План лекции.

1. 
   Метод наискорейшего градиентного спуска. Основные понятия.
   
2. 
   Построение коэффициента спуска. Теорема о сходимости.
   
3. 
   Проблема собственных значений.
   
4. 
   Особенности задачи о собственных значениях.
   

Метод наискорейшего градиентного спуска.Рассмотрим СЛАУ с положительно определенной симметричной матрицей: АХ=bПусть 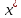- решение системы. Рассмотрим функцию 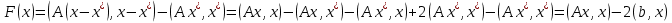, так как 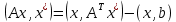.Поскольку A – положительно определена имеет место (Ax, x)≥0 для каждого x, => 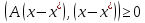и F(x) имеет минимум при 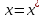, Таким образом задача поиска минимума функции F(x) равносильна решению СЛАУ.Будем рассматривать задачу минимизации функции F, приближения к решению будем получать итерационным образом 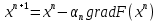;Так как 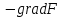– вектор , означающий направление наискорейшего убывания 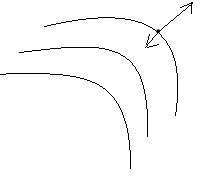Линия уровня F(x)Требуется выбрать параметр 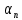, это можно сделать по-разному. Например, из условия минимизации получающегося 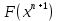, т.е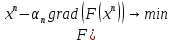В этом случае мы получим метод, называемый методом наискорейшего градиентного спуска.Найдем параметр 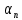. 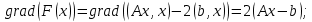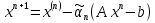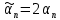Имеем: тогда ; Обозначим ϕ 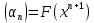неизвестное- параметр 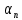.Вычислим ϕ

---

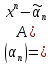
(A 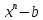)); 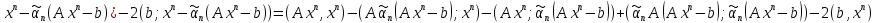+2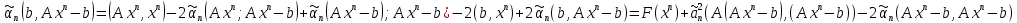

Минимум будет достигаться при

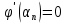
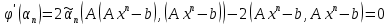; тогда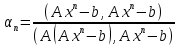



Теорема (о скорости сходимости)

Пусть собственные числа матрицы А удовлетворяют соотношению 0≤m<λ .

Тогда при любом выборе начального приближения метод наискорейшего спуска сходится и верна следующая оценка погрешности



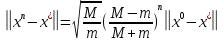
Таким образом, метод сходится со скоростью геометрической прогрессии со знаменателем

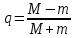
Метод требует на каждом шаге 2 умножений матрицы на вектор 2 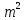опер.

Можно преобразовать вычисление формулы =>

,

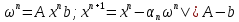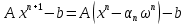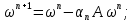
Тогда ;

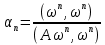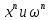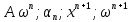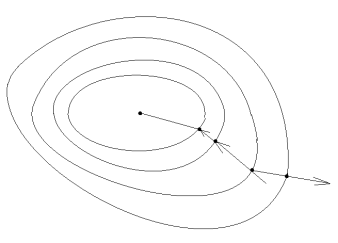
В процессе итераций запоминаются векторы , на каждом шаге последовательно вычисляются (на одно умножение меньше)

Геометрическая интерпретация метода:

F(x) – положительно опр. квадратичная форма, линии уровня F(x) – эллипсоиды, (при m=2 - эллипсы). Движемся в направлении, противоположном градиенту до точки с наименьшим значением на этой прямой



Глава 2.

Задача о собственных значениях..

Проблема собственных значений.

Рассмотрим матрицу А(m x m) как линейный оператор, задающий минимальное преобразование векторного пр-ва y = Ax.

Если 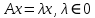, где А – ненулевая матрица, λ – число, то λ – собственное число, а x – собственный вектор.

---

Данное равенство можно переписать в виде 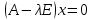→ необходимо, чтобы определитель был = 0: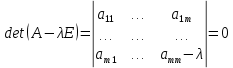Если раскрыть определитель, то получаем множители степени m относительно λ, т.е. 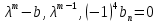, λi – корень – собственное число. Ранг матрицы 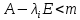. Система имеет не единственное решение. Выбираем все варианты, являющиеся решением, это и будет собственный вектор.Если 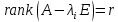, n - r = k, то данному собственному числу соответствует k, линейно независимых собственных векторов.Обычно удобно преобразовывать матрицу прежде чем вычислять собственные числа и векторы.Матрица А в некоторой системе координат (х, у) осуществляет преобразование Ах = у. В другой системе координат (ζ, η) это же преобразование осуществляется матрицей S: 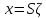, тогда т.к. y = Ax. 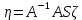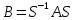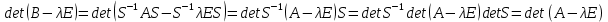Sη = Asζ, , т.е .Матрицы A и B называются подобными.Теорема:Подобные матрицы имеют одинаковые характеристические полиномы (соответственно одинаковые характеристические числа).Действительно: Следствие: подобные матрицы имеют одинаковое собственное число, включая их кратность.Мы рассмотрим методы отыскания собственных чисел и векторов. В некоторых задачах требуется получиться все собственные числа, а иногда и все собственные векторы – это полная проблема собственных значений. В других случаях нужно найти какое-то собственное число (максимальное, наиболее к какому-то значению и пр.) – это частичная проблема собственных значений. Вторая задача не является частным случаем первой, т.к. нет смысла каждый раз находить все. Чем сложна задача нахождения собственных векторов и собственных чисел? Если вычислить характеристический полином 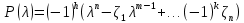, необходимо вычислить все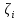

---

. Такое вычисление требует 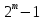вычислений определителей разного порядка. Для больших матриц это сложно. Кроме того, задача решения алгоритмического уравнения высокой степени сложны и плохо обусловлены.

Примерно до середины XX-го века строились методы, рассчитанные на быстрое вычисление корней характеристического многочлена, а далее искались его решения. Такие методы назывались прямыми. Такие методы для больших матриц очень неэффективны, по указанным выше причинам.

В настоящее время разработано много итерационных методов, в которых после преобразований матрицы мы получаем в явном виде собственные числа.

Контрольные вопросы.

1. 
   В чём суть метода наискорейшего градиентного спуска для решения СЛАУ?
   
2. 
   Для систем с какими матрицами применяется метод наискорейшего градиентного спуска?
   
3. 
   Какой функционал минимизируется в методе наискорейшего спуска для СЛАУ вида AX=b?
   
4. 
   Из каких условий выбирается шаг спуска?
   
5. 
   Каковы условия сходимости метода наискорейшего градиентного спуска для решения СЛАУ?
   
6. 
   Каковы недостатки метода наискорейшего градиентного спуска для решения СЛАУ?
   
7. 
   Что такое полная проблема собственных значений?
   
8. 
   Что такое частичная проблема собственных значений?
   
9. 
   В чём сложность задачи о собственных значениях?
   
10. 
    Какие преобразования можно совершать с матрицей, чтобы её собственные числа не изменились?
    

---

Смотрите также файлы

• Организация транспортного обеспечения в коммерческой деятельности торгового предприятия.rtf

• Книга продаж.docx

• Организационная структура компании с двумя филиалами может выглядеть следующим образом.docx

• сравнительная оценка качества питьевого молока разных производителей.docx

• Абстрагирование.docx