Уравнения и неравенства с параметрами

Линейные уравнения с параметрами

Линейным уравнением с параметром называется уравнение вида ax = b, где aи b – выражения, зависящие от параметров, а x – неизвестное.

Схема исследования:

 при a 0 уравнение имеет единственный корень x = ;

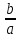 при 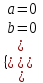, 0∙x = 0 (истина)  x = (; ), бесконечное множество решений;

 при , 0∙x = b (ложь)  нет корней.

Выбор параметра без ограничений на решение

1) Решить уравнение ax – 2 = 6x + a

▼ После преобразования: (a - 6)x = a + 2

При a  6  x =

При a = 6 уравнение примет вид 0∙x = 8 (ложь)  нет корней.

Отв. при a  6, x = ; при a = 6 корней нет.

2) Решить уравнение b²x – 7 = 49x + b

▼ После преобразования: (b + 7)(b - 7)x = b + 7

Рассмотрим два случая:

а) (b + 7)(b - 7)  0, b  7  x =

б) (b + 7)(b - 7) = 0

при b = 7, 0∙x = 14 (ложь)  нет корней

при b = -7, 0∙x = 0 (ист)  x = (; )

Отв. при b  7, x = 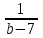; при b = 7 нет корней; при b = -7, x = (; )

3) Решить уравнение

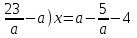
▼ ОДЗ уравнения: a  0.

При a  0 после преобразования (5 - a)(5 + a)x = (a - 5)(a + 1)

Рассмотрим два случая:

а) (5 - a)(5 + a)  0, a  5  x = -

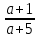
б) (5 - a)(5 + a) = 0

при a = 5, 0∙x = 0 (ист)  x = (; )

при a = -5, 0∙x = 40 (ложь)  нет корней

Отв. при a  5, x =- 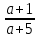; при a = 0; -5 нет корней; при а = 5, x = (; )

Выбор параметра с учетом ограничений на решение

---

1) При каком значении параметра а уравнение ах = 1 - х не имеет решения.

▼ После преобразования: (а + 1)х = 1

При а + 1= 0, а = - 1, 0∙x = 1(ложь)  нет корней. Отв. при а = - 1 нет решения.

2) При каком значении параметра а уравнение (а² – 4)х = а²+ a – 6 а) имеет бесконечно много решений; б) не имеет решения.

▼ а) имеет бесконечно много решений, если

, , а = 2

а) не имеет решения, если

, , а = -2

Отв. при а = 2, x = (; ); при а = -2 нет решения

3) При каком значении параметра а уравнение имеет единственное решение

▼ ОДЗ уравнения: a  0.

При a  0 после преобразования: (а - 2)х = 4

При а – 2  0, a  0 уравнение имеет единственное решение.

Отв. при всех а, кроме а = 0; 2

4) Решить уравнение

▼ ОДЗ уравнения: 3a - х  0, х  3a

Преобразуем уравнение: (а + 2)х = 6а

При а + 2  0, а  -2  х = .

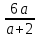Подставим х = 3a в уравнение (а + 2)х = 6а, тем самым найдем а, при котором решение хОДЗ

(а + 2)3а = 6а  а = 0

Отв. при a  0; -2, х = 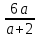; при a  0; -2 нет решений

5) Решить уравнение при всех значений параметра а



▼ ОДЗ уравнения: 5а – 6  0, a 

При a  после преобразования

При a = 2, 0∙x = 0 (ист)  x = (; )

При a = 3, 0∙x = 1(ложь)  нет корней

Отв. при a = ; 3 нет корней; при а = 2, x = (; )

6) При каких значениях параметра а уравнение 10x – 15a= 13 – 5ax + 2a имеет корень больше 2.

▼ После преобразования: 5(

---

а + 2)х = 17а + 13

При а + 2  0, a  -2  x = 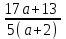. По условию х > 2, или

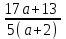> 2, 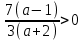 (a- 1)(a + 2) > 0  x < -2, x > 1

Отв. (-;-2)(1;)

7) При каких значениях n уравнение (n² - 16)х + n² – 3n – 4 = 0 имеет корень больше 1.

▼ После преобразования: (n – 4)(n + 4)х = -(n + 1)(n - 4)

При (n – 4)(n + 4), n  4  x = - . По условию х > 1, или

- > 1, 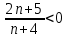 (2n+ 5)(n + 4) < 0  n(-4; -2,5)

При n= 4, 0∙x = 0 (ист)  x = (; ), в том числе х > 1

Отв.n(-4; -2,5)4

8) При каких целых значениях параметра а корень уравнения (а - 5)х + а = 3 лежит в промежутке 0; 5.

▼ После преобразования: (а - 5)х = 3 – а

При а – 5  0, a  5  x = 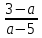. По условию 0  х  5, или

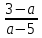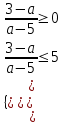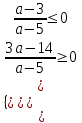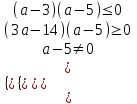0   5  , , , 3  a 

На этом отрезке находятся только два целых числа 3; 4- решение

Отв. 3; 4

9) При каких значениях параметра а уравнение имеет положительные решения.

▼ ОДЗ уравнения: ,

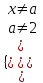
В ОДЗ уравнение равносильно 2ax = 3a² – a – 2

При a = 0, 0∙x = -2(ложь)  нет решения

При а  0; 2  x = .

Подставим х = а в уравнение 2ax = 3a² – a – 2, тем самым найдем а, при котором решение xОДЗ

a² – a – 2 = 0, a =-1; 2

Таким образом, при a =-1; 0; 2 исходное уравнение не имеет решения.

При a  -1; 0; 2 уравнение имеет единственное решение

---

x = .

Это решение будет положительным (x > 0), если

> 0  (3a² – a – 2)a > 0, (a + 2/3)a(a - 1) > 0



Из найденного множества значений параметра а исключаем a = 2

Отв. (-2/3; 0)(1; 2)(2; )
Линейные неравенства с параметрами

При решении неравенств учитываем, что при делении неравенства на положительное число знак неравенства сохраняется, а при делении на отрицательное – меняется но противоположный.

1) Решить неравенство ax < b

▼ Рассмотрим случаи a = 0, a > 0, a < 0.

Значение параметра b является существенным только при a = 0

При , 0∙х < b (ист), x = (; )

При , 0∙х < b (ложь), нет решений

При a > 0, х < , при a < 0, х > .

Отв. при a = 0, b> 0, x = (; ); при a = 0, b 0 решений нет; при a > 0,

х < ; при a < 0, х > .

2) Решить неравенство ax  b

▼ Рассмотрим случаи a = 0, a > 0, a < 0.

Значение параметра b является существенным только при a = 0

При , 0∙х  b(ложь), нет решений

При , 0∙х  b (ист), x = (; )

При a > 0, х  , при a < 0, х  .

Отв. при a = 0, b> 0 решений нет; при a = 0, b 0, x = (; ); при a > 0,

х  ; при a < 0, х  .

3) Решить неравенство ax – 2x > 4

▼ Преобразованное неравенство: (a – 2)x > 4

При a – 2 = 0, a = 0, 0∙х > 4(ложь), нет решений

---

При a – 2 > 0, a > 2, х >

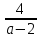
При a – 2 < 0, a < 2, х <

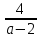
Отв. при a = 2 нет решений; при a > 2, х > 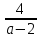; при a < 2, х <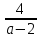

4) Решить неравенство 3a(a– 3)x > a - 3

▼ Нужно рассмотреть случаи, когда коэффициент 3a(a– 3) при х равен нулю, положителен и отрицателен



При a = 0, 0∙х > -3 (ист), x = (; )

При a = 3, 0∙х > 0 (ложь) нет решений

При a < 0, a > 3, x >

При a(0; 3), x <

Отв. при a = 0, x = (; ); a = 3 нет решений; при a < 0, a > 3, x > ; при a(0; 3), x <

5) При каких значениях параметра а неравенство 2a(a – 2)x > a – 2 а) не имеет решения; б) выполняется при любых значениях х

▼ а) неравенство не имеет решения, когда

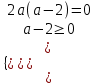, , а = 2

б) неравенство выполняется при любых значениях х, когда

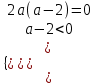, , а = 0

Отв. а) 2; б) 0

6) При каком значении параметра а неравенство a²x < a + x а) не имеет решения; б) выполняется при любых значениях х

▼ Преобразованное неравенство (a² – 1)x < a

а) неравенство не имеет решения, когда

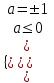, , а =-1

б) неравенство выполняется при любых значениях х, когда

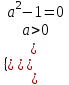, , а =1

Отв. а) -1; б) 1

7) Решить неравенство

---

Смотрите также файлы

• Студенты это будущее каждой страны. Это молодые граждане нашего общества, полные безграничной энергии и прогрессивных идей, фантастических планов и благородных амбиций, надежд и мечтаний.rtf

• Практическая работа 1 Задание 5 Единица уровня Функции единицы Уровень, подуровни.docx

• Вопросы для итогового контроля.doc

• московский междунaродный университет.docx

• Методические указания по выполнению выпускной квалификационной работы для студентов специальности 38. 02. 03 Операционная деятельность в логистике.pdf