Файл: Уравнения и неравенства с параметрами Линейные уравнения с параметрами.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 43
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
▼ ОДЗ: а – 1 0, а 1
Преобразованное неравенство:
Определим знак дроби
при различных значениях а
Если a = 4, 0∙х >
(ложь), решения нетПри а(-; 1)(4; ),
При а(1; 4),
Отв. при a = 1; 4 решения нет; при а(-; 1)(4; ),
;при а(1; 4),
8) При каких а неравенство 3x – 2a > 0 является следствием неравенства
x – 1 + a > 0
▼ Первое неравенство является следствием второго, если множество решений х1 первого неравенства содержит множество решений х2 второго неравенства. Обозначение (II неравенство)(I неравенство)
Решение первого неравенства:
, т.е. х1(
; )Решение второго неравенства: х2 > 1 – a
Включение х2х1 выполняется, если 1 – а
, т.е. а 
. Отв. а .9) При каких а неравенство 2x + 1 < x + 2a и x – 2a – 3 < 2a равносильны.
▼ Решим каждое неравенство
2x + 1 < x + 2a, x < 2a - 1
x – 2a – 3 < 2a, x < 4a + 3
У равносильных неравенств множество их решений совпадают.
Найдем а, решив уравнение:
2a - 1 = 4a + 3, a =-2, Отв. -2
10). При каких значениях а неравенство x 2a + 3 верно при всех х, удовлетворяющих условию -3 х -а – 2
▼ Достаточно решить систему
, 
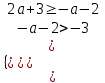, а-
; 1). Отв. -
; 1).11). При каких значениях а неравенство 2x – a + 4 < 0 верно при всех х, удовлетворяющих условию 3 х 5
▼ Преобразованное неравенство: 2x < a – 4,
, х(-; 
).Отрезок 3; 5 принадлежит промежутку (-;
), если > 5, a > 14. Отв. а(14; )