Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная/очно-заочная

ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕЭКОНОМЕТРИКАГруппа Ом20Э271СтудентН.А. КорзунМОСКВА 2022ЗАДАНИЕ ПО ПРАКТИЧЕСКОЙ РАБОТЕВопросы:

1. 
   Укажите основные этапы эконометрического исследования.
   

Можно выделить шесть основных этапов:

• 
  Постановки задачи;
  
• 
  Разработка теоретической модели;
  
• 
  Сбор данных;
  
• 
  Оценка параметров;
  
• 
  Апробация и интерпретация результатов;
  
• 
  Сопровождение модели.
  

2. 
   Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей.
   

В линейной модели параметры bi при факторах хi характеризуют величину среднего изменения зависимой переменной y с изменением соответствующего фактора хi на единицу, в то время как значения остальных факторов остаются неизмененными.В степенной модели параметры bj при факторах хi являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменяется зависимая переменная y при изменении соответствующего фактора хi на 1 % в условиях неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.

3. 
   Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии.
   

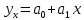
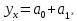
Линейная Показательная Полулогарифмическая

---

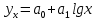
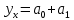
Гиперболическая Степенная

4. 
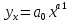
   Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции r_xy.
   

5. 
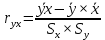
   Объясните сущность метода анализа динамического ряда.
   

Анализ динамического ряда включает в себя расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому, и также нахождение обобщенных средних характеристик, а также выявление основных закономерностей в развитии динамического ряда.Задачи:

1. 
   Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3
   

Таблица 3. Регрессионный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

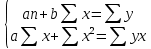
Система нормальных уравненийЛинейная зависимость

x	y		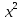	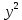xy
10	30	100	900	300
20	50	400	2500	1000
30	70	900	4900	2100
40	90	1600	8100	3600
50	110	2500	12100	5500
150	350	5500	28500	12500

---

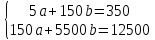домножим 1-е уровнение на (-30)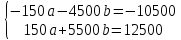1000b=13280b=13,28найдем а5а+150*13,28=3505а=350-1992=-1642а=-328,4Уравнение линейной регрессииУ=13,28х-328,4Экспоненциальная зависимость

х	lny			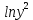x*lny
10	3,4012	100	6,8024	34,012
20	3,9120	400	7,8240	78,24
30	4,2485	900	8,497	127,455
40	4,5	1600	8,9996	180
50	4,7004	2500	9,401	235,02
150	20,7621	5500	41,524	654,727

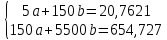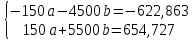
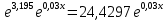
домножим 1-е уровнение на (-30)1000b=31,864b=0,0319найдем а5а+150*0,0319=20,76215а=20,7621-4,785=15,9771а=3,1954уравнение экспоненциальной зависимостиу=Степенная зависимость

lnх	lny		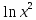	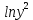lnx*lny
2,3026	3,4012	4,6052	6,8024	7,8316
2,9957	3,9120	5,9915	7,8240	11,7192
3,4012	4,2485	6,8024	8,497	14,45
3,6889	4,5	7,3778	8,9996	16,6
3,9120	4,7004	7,8240	9,401	18,388
16,3004__20,7621__32,6009__41,524'>16,3004	20,7621	32,6009	41,524	68,9888

---

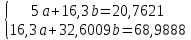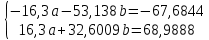
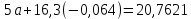
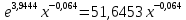
домножим 1-е уровнение на (-3,26)-20,54b=1,3044b=-0,064найдем а5а=20,7621-1,0432=19,7189а=3,9444Уравнение степенной зависимостиу=Логарифмическая зависимость

lnх	у			lnx*y
2,3026	30	4,6052	900	69,078
2,9957	50	5,9915	2500	149,785
3,4012	70	6,8024	4900	238,084
3,6889	90	7,3778	8100	332,001
3,9120	110	7,8240	12100	430,32
16,3004	350	32,6009	28500	1219,268

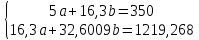домножим 1-е уровнение на (-3,26)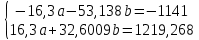-20,5371b=78,268b=-3,86найдем а5а+16,3*(-3,86)=3505а=412,918а=82,58Уравнение логарифмической зависимостиу=-3,86lnx+82.58Показательная зависимость

x	lny			lnу*х
10	3,4012	100	6,8024	34,012
20	3,9120	400	7,8240	78,24
30	4,2485	900	8,497	127,455
40	4,5	1600	8,9996	180
50	4,7004	2500	9,401	235,02
150	20,7621	5500	41,524	654,727

---

домножим 1-е уровнение на (-30)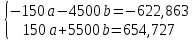1000b=31,864b=0,032найдем а5а+150*0,032=20,76215а=15,96а=3,192Уравнение показательной зависимостиу=

2. 
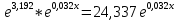
   Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4.
   

Таблица 4. Корреляционный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

x	y			xy
10	30	100	900	300
20	50	400	2500	1000
30	70	900	4900	2100
40	90	1600	8100	3600
50	110	2500	12100	5500
150	350	5500	28500	12500

---

Смотрите также файлы

• Практическая работа 1 Задача 1.docx

• Классы моделей в тпр.pptx

• Методические указания по выполнению выпускной квалификационной работы для бакалавров, обучающихся по направлению.docx

• В целом Су Синчэнь был позитивным и оптимистичным человеком.docx

• Тест дкб наращенная сумма простых процентов определяется по формуле.docx