Задача 1. На тонком стержне длиной L равномерно распределен электрический заряд Q. На продолжении оси стержня на расстоянии a от ближайшего конца расположен точечный заряд q, который взаимодействует с зарядом на стержне с силой F. Линейная плотность заряда на стержне τ. Определите величину, указанную в таблице знаком вопроса.

№ варианта	L, м	a, м	q ∙ 10-9 Кл	F∙ 10-6, Н	τ ∙ 10-9 Кл/м	Q ∙ 10-9 Кл
6	∞	0,10	4,0	?	12,5	‒

Решение:

Сила взаимодействия F заряженного стержня с точечным зарядом Q₁ зависит от линейной плотности τ заряда на стержне. Зная эту зависимость, можно определить τ. При вычислении силы F следует иметь в виду, что заряд на стержне не является точеч­ным, поэтому закон Кулона непосредственно применить нельзя. В этом случае можно поступить следующим образом. Выделим из стержня (рис. 1) малый участок dr с зарядом dQ = τdr. Этот заряд можно рассматривать как точечный.





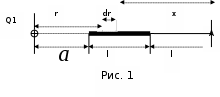
Тогда, согласно закону Кулона:

.

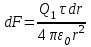Интегрируя это выражение в пределах от а до а+l,получаем:

,

.

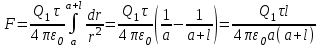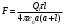Проверим, дает ли рас­четная формула единицу силы. Для этого в правую часть формулы вместо символов величин подста­вим их единицы:



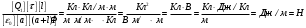
Найденная единица является единицей силы.

Произведем вычисления:



.

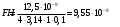
Задача 2. Два точечных электрических заряда q₁ и q₂ находятся в воздухе на расстоянии d друг от друга и создают в точке А поле, напряженность которого Е, потенциал φ. Точка удалена от заряда на расстояние r₁, от заряда на расстоянии r₂. Определить напряженность в точке А.

№ варианта	α, град	q1∙ 10-9 Кл	q2 ∙ 10-9 Кл	d, м	r1, м	r2, м	φ, В
6	45	‒ 1,0	‒	0,12	0,12	‒	‒ 0,9

---

Согласно принципу суперпозиции элек­трических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность 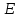электрического поля в искомой точке может быть найдена как геометрическая сумма напряженносте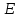й ₁ и 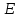₂ полей, создаваемых каждым зарядом в отдельности: 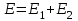. Напряженности электриче­ского поля, создаваемого в воздухе (ε=1) зарядами Q₁ и Q₂,

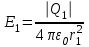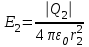; . (1)

Вектор 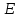₁ (рис. 1) направлен по силовой линии от заряда Q₁, так как этот заряд положителен; вектор 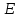₂ направлен также по силовой линии, но к заряду Q₂, так как этот заряд отрицателен.

Модуль вектора 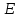найдем по теореме косинусов:

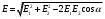, (2)

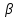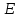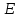где – угол между векторами ₁ и ₂, 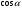= 0,707,

Подставляя выражение Е₁ и E₂ из (1) в (2) и вынося общий множитель 1/(4πε₀) за знак корня, полу­чаем

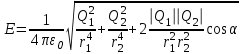. (3)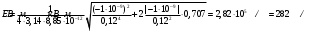


Задача 3. Две равномерно заряженные концентрические сферы с радиусами R₁ и R₂ имеют заряды соответственно q₁ и q₂.

1. Определить напряженность и потенциал, создаваемые заряженными сферами в точках а, b, и с, находящимися на расстоянии соответственно r₁, r₂

---

и r₃ от центра сфер.

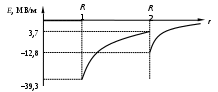
2. Построить график зависимости напряженности от расстояния E(r), взяв за начало координат центр сферы.

3. Построить график зависимости потенциала от расстояния φ(r), приняв за нулевой потенциал точку, находящуюся очень далеко от центра сфер. Числовые значения заданных величин указаны в таблице.

№ варианта	q1∙ 10-10 Кл	q2∙ 10-10 Кл	R1, см	R2, см	r1, см	r2, см	r3, см
6	1	‒ 4	1	4	0,5	3	5

Решение:



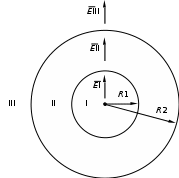
Напряженность электрического поля, создаваемого металлической сферой радиусом R₁, несущей заряд Q₁, на расстоянии r от центра сферы:

внутри сферы (r < R₁) E₁ = 0;

вне сферы, включая внешнюю поверхность сферы, r ≥ R₁



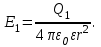
ε = 1 ‒ диэлектрическая проницаемость среды;

ε₀ = 8,85∙10⁻¹² Ф/м ‒ электрическая постоянная.

Для сферы радиуса R₂: внутри сферы (r < R₂) E₂ = 0;

вне сферы, включая внешнюю поверхность сферы, r ≥ R₂



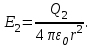
Результирующую напряженность найдем по принципу суперпозиции полей векторным суммированием:



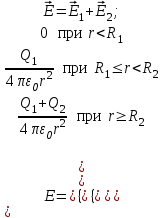
Потенциал электрического поля, создаваемого металлической сферой радиусом R₁, несущей заряд Q₁, на расстоянии r от центра сферы:

внутри сферы и на поверхности (r ≤ R₁)



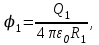
вне сферы (r > R₁)



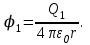
Для сферы радиуса R₂:

внутри сферы и на поверхности (r ≤ R₂)



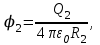
вне сферы (r > R₂)

---

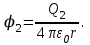
Результирующий потенциал найдем по принципу суперпозиции полей:



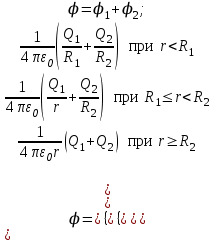
R₁ = 0,01 м; R₂ = 0,04 м.

1. 
   r = 0,005 м < R₁;
   

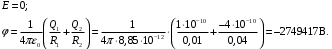
2) r = 0,03 м, R₁ < r < R₂;



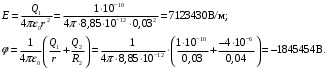
3) r = 0,05 м > R₂;



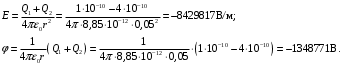
Вычислим значения напряженности на границах областей:






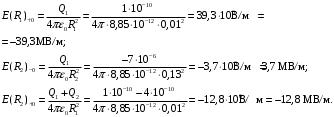
Вычислим значения потенциала на границах областей:




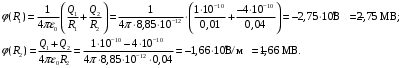
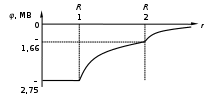
Ответ: 1) E = 0; φ = –2749417В; 2) E = –7123430В/м; φ = –1845454 В; 3) E = –8429817 В/м; φ = –1348771 В.

Задача 4. Плоский конденсатор заполнен полностью двумя слоями диэлектрика с диэлектрическими проницаемостями ε₁ и ε₂. Толщина слоев d₁ и d₂. На конденсатор подано напряжение U. Граница раздела диэлектриков параллельна обкладкам конденсатора. Возможны случаи, когда: а) конденсатор предварительно отключен от батареи: б) конденсатор все время соединен с батареей. Найти величину, указанную в таблице знаком вопроса.

№ варианта	ε1	ε2	ε1/ ε2	d1, см	d2, см	U, В	Е1·105, В/м	Е2·105, В/м
б) конденсатор все время соединен с батареей
6	2,0	6,0		2,0	4,0	‒	‒	?

Если конденсатор заполнен диэлектриком с относительной диэлектрической проницаемостью ε, то напряжённость в ε раз меньше и равна E=σ/εε

---

₀

Для нескольких параллельных пластинам слоёв диэлектриков эта формула также справедлива (поскольку линии напряжённости перпендикулярны поверхности диэлектрика), в результате чего получаем следующее выражение для напряжения
U=E₁d₁+E₂d₂=σ/ε₀·(d₁/ε₁+d₂/ε₂)
Выражаем напряжённость

E₂=σ/ε₂ε₀=U/(ε₂(d₁/ε₁+d₂/ε₂)) = U/(d₂+d₁ε₂/ε₁) ≈ 3,7 ·10³ В/м = 3,7 кВ/м
[E] = [U] /(d₂ + d₁ ∙ ε₂/ε₁) = В/м

Задача 5. Из микроамперметра с пределом измерения силы тока I₀ и сопротивлением катушки R₀ изготовляют амперметр с пределом измерения силы тока I или вольтметр с пределом измерения напряжения U путем подключения шунта сопротивлением или добавочного сопротивления Определите величину, указанную в таблице знаком вопроса.

№ варианта	I0, мА	R0, Ом	I, A	U, B	Rш, Ом	RД, Ом
6	1	0,1	1	?	?	9,9

Решение:

У вольтметра добавочное сопротивление подключается последовательно с катушкой, так что по ним протекает один и тот же ток I₀. По закону Ома:

 U = I₀ ∙ (R₀ + R_д) (1),

U = 0,001 ∙ (0,1 + 9,9) = 0,0001В

 Падение напряжения на катушке микроамперметра при токе I₀ = 1,0 ∙ 10^-3 А:

 U_к = I₀ ∙ R₀ = 1,0 ∙ 10^-3 ∙ 0,1 = 1,0 ∙ 10

---

Смотрите также файлы

• Тк 18. Задание Задание Разберите самостоятельно модель круговых потоков с государственным вмешательством в открытой экономике.docx

• Легочные синдромы.doc

• Выполнение практического задания по дисциплине анатомия.docx

• Доброе утро, Виктория!.pdf

• Лабораторная работа 2 Работа со справочноинформационными правовыми системами КонсультантПлюс иГарант.odt