Файл: Контрольная работа по дисциплине Основы научных исследований.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Забайкальский государственный университет»
(ФГБОУ ВО «ЗабГУ»)
Факультет горный
Кафедра подземной разработки месторождений полезных ископаемых
Контрольная работа
по дисциплине «Основы научных исследований»
Чита, 2023
Индивидуальное задание №7
| Номер опыта (наблюдения) | Выход негабаритов,% y | Удельный расход (фактич.) ВВ на первичную отбойку, кг/т x |
| 1 | 5,5 | 0,92 |
| 2 | 7,0 | 0,85 |
| 3 | 6,8 | 0,86 |
| 4 | 8,4 | 0,77 |
| 5 | 9,1 | 0,81 |
| 6 | 10,5 | 0,68 |
| 7 | 12,1 | 0,62 |
| 8 | 14,5 | 0,60 |
| 9 | 15,0 | 0,55 |
| 10 | 15,2 | 0,58 |
| 11 | 15,3 | 0,51 |
| 12 | 14,8 | 0,59 |
| 13 | 15,6 | 0,52 |
| 14 | 9,4 | 0,79 |
| 15 | 6,5 | 0,95 |
Уравнение парной регрессии.
На основании поля корреляции можно выдвинуть гипотезу (для генеральной совокупности) о том, что связь между всеми возможными значениями X и Y носит линейный характер.
Линейное уравнение регрессии имеет вид y = bx + a
Оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок ε
i, a и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β - используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
a·n + b·∑x = ∑y
a·∑x + b·∑x2 = ∑y·x
Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | y | x2 | y2 | x*y |
| 0.51 | 15.3 | 0.2601 | 234.09 | 7.803 |
| 0.52 | 15.6 | 0.2704 | 243.36 | 8.112 |
| 0.55 | 15 | 0.3025 | 225 | 8.25 |
| 0.58 | 15.2 | 0.3364 | 231.04 | 8.816 |
| 0.59 | 14.8 | 0.3481 | 219.04 | 8.732 |
| 0.6 | 14.5 | 0.36 | 210.25 | 8.7 |
| 0.62 | 12.1 | 0.3844 | 146.41 | 7.502 |
| 0.68 | 10.5 | 0.4624 | 110.25 | 7.14 |
| 0.77 | 8.4 | 0.5929 | 70.56 | 6.468 |
| 0.79 | 9.4 | 0.6241 | 88.36 | 7.426 |
| 0.81 | 9.1 | 0.6561 | 82.81 | 7.371 |
| 0.85 | 7 | 0.7225 | 49 | 5.95 |
| 0.86 | 6.8 | 0.7396 | 46.24 | 5.848 |
| 0.92 | 5.5 | 0.8464 | 30.25 | 5.06 |
| 0.95 | 6.5 | 0.9025 | 42.25 | 6.175 |
| 10.6 | 165.7 | 7.8084 | 2028.91 | 109.353 |
Для наших данных система уравнений имеет вид
15a + 10.6·b = 165.7
10.6·a + 7.808·b = 109.353
Получаем эмпирические коэффициенты регрессии: b = -24.3653, a = 28.2648
Уравнение регрессии (эмпирическое уравнение регрессии):
y = -24.3653 x + 28.2648
Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
=
=
Среднеквадратическое отклонение
Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно:
Коэффициент корреляции.
Ковариация.
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y и фактором X весьма высокая и обратная.
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:
Коэффициент детерминации, найденный по формуле, составляет rд=0,9752=0,951, что означает, что 95% разброса определяется изменчивостью х, а 5% — другими причинами, т. е. изменчивость функции у почти полностью характеризуется разбросом (природой) фактора х.
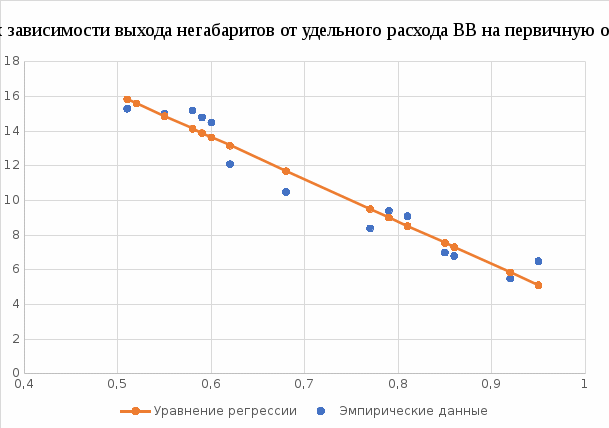
Построим ломанную регрессии по эмпирическим данным и зависимость по установленному уравнению регрессии.
Список литературы
1. Аренс, В.Ж. Основы методологии горной науки : учеб. пособие / Аренс Виктор Жанович. - Москва: МГГУ, 2003. - 223 с.
2. Основы научных исследований: учебник для вузов / Крутов Виталий Иванович [и др.]; под ред. В.И. Крутова, В.В. Попова. – Москва: Высш. шк., 1989. - 400с.
3. Лизункин, В.М. Методология научного творчества: практич. пособие / Лизункин Владимир Михайлович, Мязин Виктор Петрович, Романова Нелли Петровна. - Чита: ЧитГТУ, 2003. - 215 с.
4. Аренс, В.Ж. Основы методологии горной науки [Электронный ресурс]: Учеб. пособие / Арене В.Ж. - М: Издательство Московского государственного горного университета, 2003.