Файл: Отчет по лабораторной работе 2 математический маятник.docx
Добавлен: 30.11.2023
Просмотров: 228
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и образования Российской Федерации
ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Институт Заочно-вечернего обучения
Отчет по лабораторной работе № 3.2
«МАТЕМАТИЧЕСКИЙ МАЯТНИК»
Выполнил:
Студент, группы ____/____ (подпись) __/ И. О. Фамилия / (дата)
№ зачетной книжки ________
Принял:
Доцент кафедры физики В. И. Щепин
Иркутск – 2023
МАТЕМАТИЧЕСКИЙ МАЯТНИК
Цель работы: Определение ускорения свободного падения g при помощи математического маятника, изучение погрешностей измерений физических величин и применение на практике для оценки точности определения g.
Приборы и принадлежности: виртуальный тренажер «Математический маятник».
Теоретическая часть
Гармоническими колебаниями физической величины х называется
процесс изменения ее во времени t пo закону
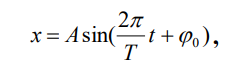
где A – амплитуда колебаний; T - период колебаний.
Величина
График таких колебаний представлен на рисунке:
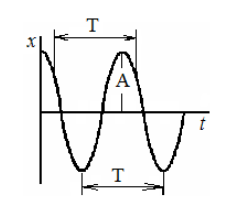
Из определения гармонических колебаний следует, что период колебаний является наименьшим промежутком времени, по истечении которого движение в точности повторяется.
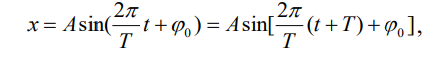
За время t = T совершается одно полное колебание.
Амплитуда колебаний Aравна максимальному значениюx.
Величина
, то уравнение гармонических колебаний можно записать в виде
Для изучения гармонических колебаний можно воспользоваться математическим маятником.
Математический маятник – это (модель) идеализированная система, состоящая из материальной точки массой m, подвешенной на длинной нерастяжимой нити l, и совершающая колебания около положения равновесия.
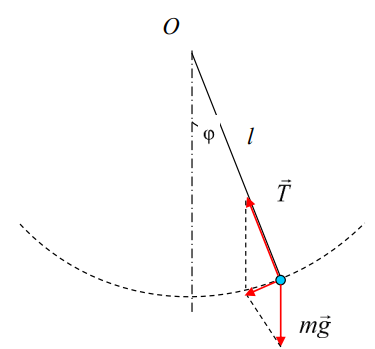
Достаточно хорошим приближением к математическому маятнику служит небольшой тяжёлый шарик диаметром, подвешенный на длинной тонкой нерастяжимой нити при выполнении условия d<<l. Длина маятника l равна расстоянию от точки подвеса до центра тяжести шарика. Можно показать, что шарик, отклонённый на угол от положения равновесия, бедет совершать гармонические колебания. На него действует возвращающая квазиупругая сила, составляющая силы тяжести. Уравнение динамики вращательного движения для этих условий можно записать в виде
Для малых углов отклонения sinφ φ . С учетом того, что для шарика на нити можно принять
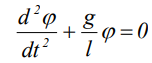 .
.Это уравнение аналогично общему уравнения гармонических колебаний при условии, что собственная частота колебаний системы
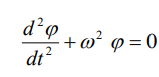
Можно показать, что частным решением последнего дифференциального уравнения является уравнение
и периодом
Период колебаний маятника – это время, в течение которого маятник совершает одно полное колебание и возвращается в исходную точку. Для определения ускорения свободного падения можно воспользоваться предыдущим выражением , если решить его относительно g:
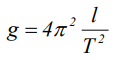
Достаточно измерить период колебаний Т и длину маятника l, чтобы рассчитать по этой формуле ускорение свободного падения.
Так как g – величина постоянная для данной географической точки, то видно, что при заданной длине маятника l период колебаний маятника Т представляет собой постоянную величину. Поэтому при неоднократном измерении времени t одного и того же количества N колебаний, казалось бы, должен получаться неизменный результат. Однако даже при использовании сравнительно точного прибора (например, электронного секундомера) можно убедиться в том, что от опыта к опыту значение t изменяется то в большую, то в меньшую сторону. Различия в результатах измерения одной и той же величины объясняются случайными погрешностями.
Изучение погрешностей измерений и расчётов является одной из главных целей данной лабораторной работы.
Описание экспериментальной установки
Схема экспериментальной установки и входящие в неё приборы и принадлежности приведены на рисунке ниже
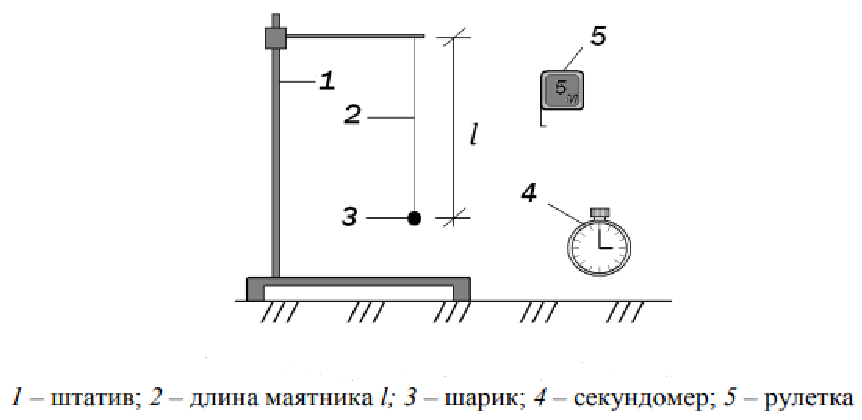


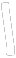








Вариант №73
Выполняем лабораторную работу в соответствии с приведенным порядком, измерения повторяем пять раз для различных значений числа колебаний n1, n2, n3, …
Таблица результатов измерений
| i | l, см | 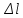 , мм , мм | n | t, с | 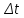 , с , с | 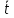 , с , с | Т, с | 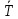 , с , с | 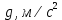 | 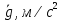 |
| 1 | 130 | 5 | 10 | 22,71 | 0,01 | 27,38 | 2,271 | 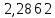 | 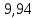 | 9,81 |
| 2 | 11 | 25, 69 | 2,354 | 9.25 | ||||||
| 3 | 12 | 27,2 | 2,267 | 9,97 | ||||||
| 4 | 13 | 29,36 | 2,258 | 10,056 | ||||||
| 5 | 14 | 31,94 | 2,281 | 9,85 |
Вычисления
Период колебания маятника:
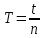
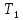 = 22,71 / 10 = 2,271 c
= 22,71 / 10 = 2,271 c 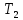 = 25, 69 / 11 ≈ 2,354 c
= 25, 69 / 11 ≈ 2,354 c 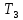 = 27,2 / 12 ≈ 2,267 c
= 27,2 / 12 ≈ 2,267 c 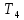 = 29,36 / 13 ≈ 2,258 c
= 29,36 / 13 ≈ 2,258 c 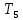 = 31,94 / 14 ≈ 2,281 c
= 31,94 / 14 ≈ 2,281 c Среднее значение периода колебаний:
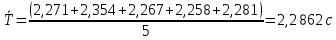 ;
; Ускорение свободного падения:
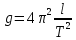
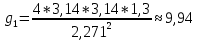
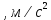
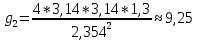
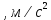
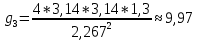
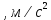
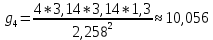
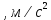
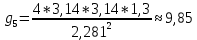
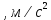
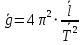
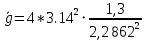 ≈ 9,81
≈ 9,81 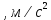
| I | T, с | 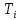 , с , с | 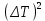 , с * , с *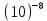 | 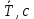 | P | 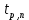 | S , с | 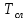 , с , с |
| 1 | 2,271 | 0,0318 | 23104 | 2, 2862 | 0,95 | 2,78 | 173,476 * 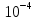 | 0,048 |
| 2 | 2,354 | 0,0188 | 459684 | |||||
| 3 | 2,267 | -0,0342 | 36864 | |||||
| 4 | 2,258 | -0,0412 | 79524 | |||||
| 5 | 2,281 | 0,0248 | 2704 |
Абсолютная погрешность измерения времени:
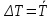 –
–