ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ошибка обучения для построенной нейронной сети вычисляется путем сравнения выходных и целевых (желаемых) значений. Из полученных разностей формируется функция ошибок.
Функция ошибок - это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети.
С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения.
От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задач
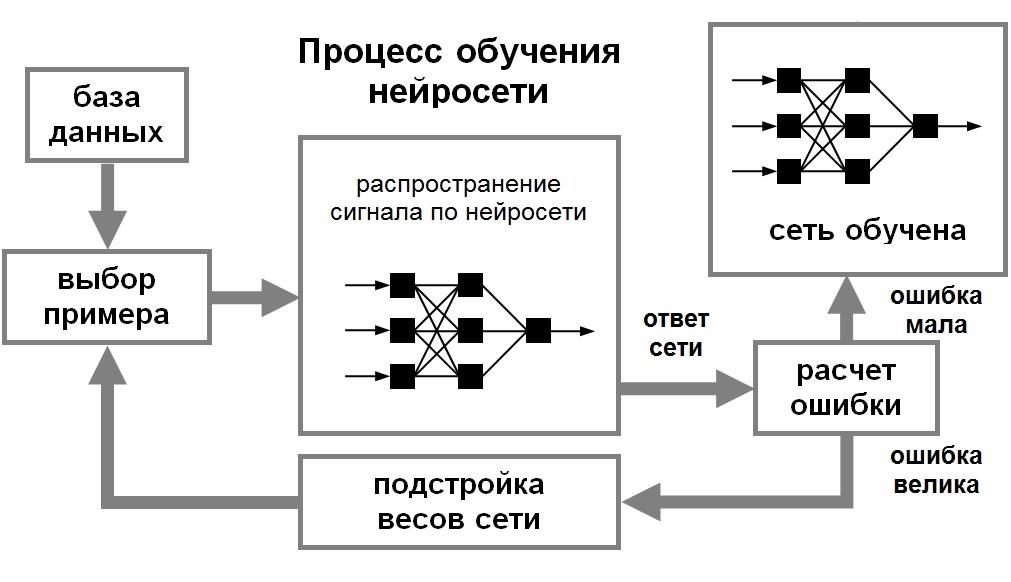
Процесс обучения нейронной сети
Алгоритмы обучения нейронной сети
Обучение с учителем
Обучение без учителя
Сбор данных для нейронной сети
Требования к обучающему множеству:
➢Множество не должно содержать всплесков – элементы, свойства которых отличаются от ожидаемых значений;
➢Элементы множества должны быть репрезентативны;
➢Обучающая выборка должна быть в несколько раз больше общего количества
весовых связей в сети;
➢Частные требования.
Выводы:
➢Выбирайте такие переменные, которые, как Вы предполагаете, влияют на результат.
➢С числовыми и номинальными переменными можно работать непосредственно. Переменные других типов следует преобразовать в указанные типы или объявить незначащими.
➢Чем больше в задаче переменных, тем больше нужно иметь наблюдений.
➢ В случае необходимости можно работать с наблюдениями, содержащими пропущенные значения. Если возможно, удалите выбросы. Если данных достаточное количество, уберите из рассмотрения наблюдения с пропущенными значениями.
Подготовка данных для обучения
➢Количество наблюдений в наборе данных. Следует учитывать тот фактор, что чем больше размерность данных, тем больше времени потребуется для обучения сети. ➢Работа с выбросами. Следует определить наличие выбросов и оценить необходимость их присутствия в выборке.
➢Обучающая выборка должна быть представительной (репрезентативной). ➢Обучающая выборка не должна содержать противоречий, так как нейронная сеть однозначно сопоставляет выходные значения входным.
➢Нейронная сеть работает только с числовыми входными данными, поэтому важным этапом при подготовке данных является преобразование и кодирование данных. При использовании на вход нейронной сети следует подавать значения из того диапазона, на котором она обучалась. Например, если при обучении нейронной сети на один из ее входов подавались значения от 0 до 10, то при ее применении на вход следует подавать значения из этого же диапазона или близлежащие.
Существует понятие нормализации данных.
Целью нормализации значений является преобразование данных к виду, который наиболее подходит для обработки, т.е. данные, поступающие на вход, должны иметь числовой тип, а их значения должны быть распределены в определенном диапазоне.
Нормализатор может приводить дискретные данные к набору уникальных индексов либо преобразовывать значения, лежащие в произвольном диапазоне, в конкретный диапазон, например, [0..1].
Нормализация выполняется путем деления каждой компоненты входного вектора на длину вектора, что превращает входной вектор в единичный.
Выбор структуры нейронной сети
Выбор структуры нейронной сети обусловливается спецификой и сложностью решаемой задачи. В большинстве случаев выбор структуры нейронной сети определяется на основе объединения опыта и интуиции разработчика.
Однако существуют основополагающие принципы, которыми следует руководствоваться при разработке новой конфигурации :
➢возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев;
➢введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;
➢сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов - возбуждающих, тормозящих и др.) также способствует усилению мощи НС.
Переобучение нейронной сети
При обучении нейронных сетей часто возникает серьезная трудность, называемая проблемой переобучения
Переобучение - излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению.
возникает в случае слишком долгого обучения, недостаточного числа обучающих примеров или переусложненной структуры нейронной сети.
связано с тем, что выбор обучающего множества является случайным. С первых шагов обучения происходит уменьшение ошибки. На последующих шагах с целью уменьшения ошибки параметры подстраиваются под особенности обучающего множества. Однако при этом происходит "подстройка" не под общие закономерности ряда, а под особенности его части - обучающего подмножества. При этом точность прогноза уменьшается.
Переобучение нейронной сети
Один из вариантов борьбы с переобучением сети - деление обучающей выборки на два множества (обучающее и тестовое).
На первом шаге ошибки прогноза для обучающего и тестового множества одинаковы. На последующих шагах значения обеих ошибок уменьшаются, однако с семидесятого шага ошибка на тестовом множестве начинает возрастать, т.е. начинается процесс переобучения сети.
Сложности применения НС
➢Для построения модели объекта на основе НС требуется выполнение многоцикловой настройки внутренних элементов и связей между ними;
➢ Проблемы, возникающие при подготовке обучающей выборки, связанные с трудностями нахождения достаточного количества обучающих примеров;
➢Обучение сети в ряде случаев приводит к тупиковым ситуациям; ➢Продолжительные временные затраты на выполнение процедуры обучения зачастую не позволяют применять ИНС в системах реального времени;
➢ Поведение обученной ИНС не всегда может быть однозначно предсказуемо, что увеличивает риск применения ИНС для управления дорогостоящими техническими объектами;
➢Обучить и эксплуатировать нейронную сеть для решения многих задач, как правило, может и не специалист, но надежно интерпретировать результаты, а также численно оценивать значимость получаемых прогнозов способны специалисты, имеющие навыки в моделировании нейронных сетей.
Модели нейронных сетей
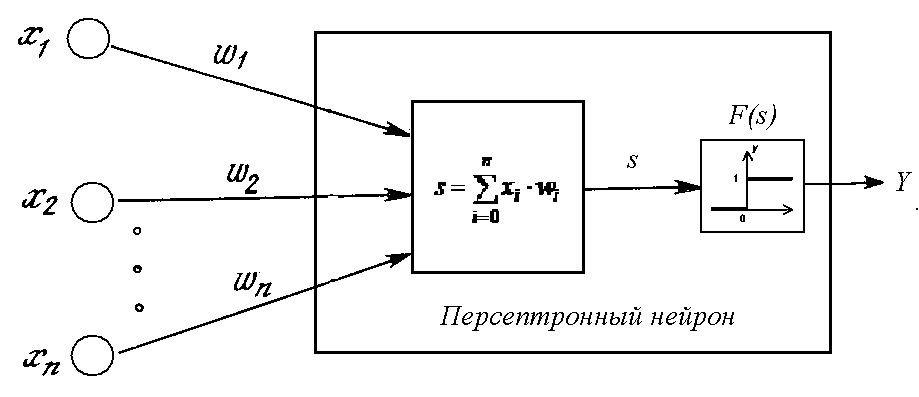
Персептрон
Большое количество моделей персептрона рассмотрено в основополагающей работе Розенблатта.
Простейшая модель
нейронной сети - однослойный персептрон.
Однослойный персептрон (персептрон Розенблатта) - однослойная нейронная сеть, все нейроны которой имеют жесткую пороговую функцию активации. Однослойный персептрон имеет простой алгоритм обучения и способен решать лишь самые простые задачи.
Классический пример такой нейронной сети - однослойный трехнейронный персептрон.
Перцептрон Розенблатта
Модель Мак-Каллока – Питтса была реализована Фрэнком Розенблаттом: в 1958 г. в виде компьютерной модели (перцептрона), в 1960 г. в виде электронного устройства, распознававшего рукописные изображения некоторых букв и цифр – первого в мире нейрокомпьютера Марк-1.
Однослойный персептрон
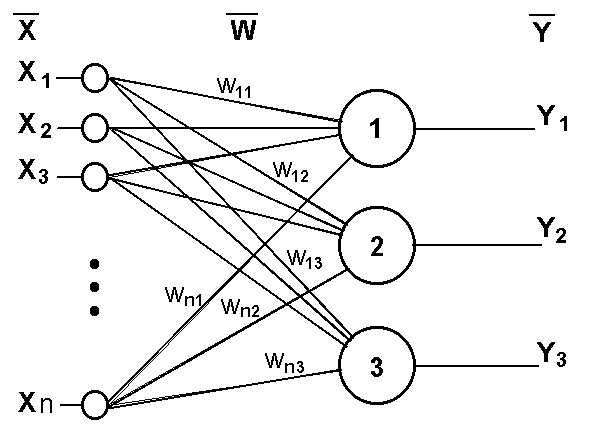
Сеть, изображенная на рисунке, имеет ???? входов, на которые поступают сигналы, идущие по синапсам на 3 нейрона. Эти три нейрона образуют единственный слой данной сети и выдают три выходных сигнала.
Алгоритм обучения персептрона

Многослойный персептрон
Многослойный персептрон (MLP) - нейронная сеть прямого распространения сигнала в которой входной сигнал преобразуется в выходной, проходя последовательно через несколько слоев.
В этой модели персептрона должен быть хотя бы один скрытый слой. Присутствие нескольких таких слоев оправдано лишь в случае использования нелинейных функций активации.
Двухслойный перцептрон
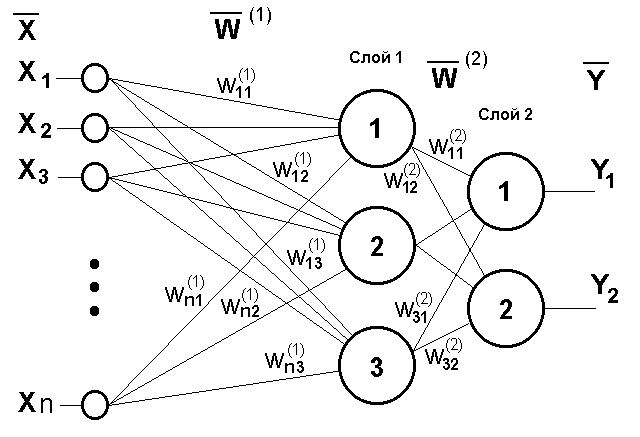
Сеть, изображенная на рисунке, имеет n входов. На них поступают сигналы, идущие далее по синапсам на 3 нейрона, которые образуют первый слой. Выходные сигналы первого слоя передаются двум нейронам второго слоя. Последние, в свою очередь, выдают два выходных сигнала.
Многослойных персептрон
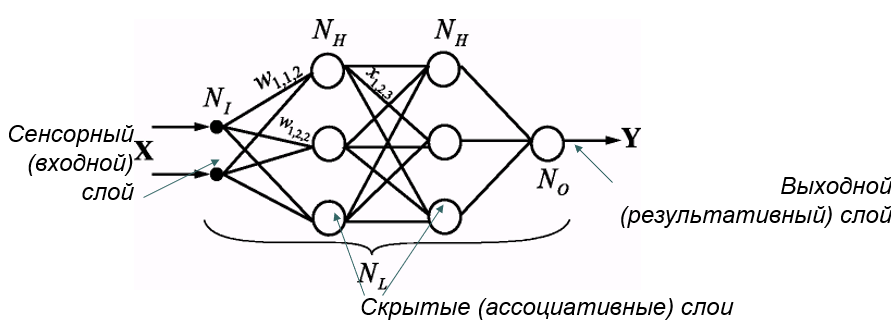
Обучение многослойного персептрона
➢Принцип связи между нейронами - "каждый с каждым".
➢Количество нейронов в слоях может быть произвольным.
➢Обычно во всех скрытых слоях одинаковое количество нейронов.
➢Входной слой только распределяет сигналы.
Целью обучения является поиск таких значений весов и порогов сети, которые бы минимизировали ошибку прогноза, выдаваемого сетью.
Функции ошибок:
➢сумма квадратов ошибок; ➢среднеквадратическая ошибка.
Многослойные нейронные сети
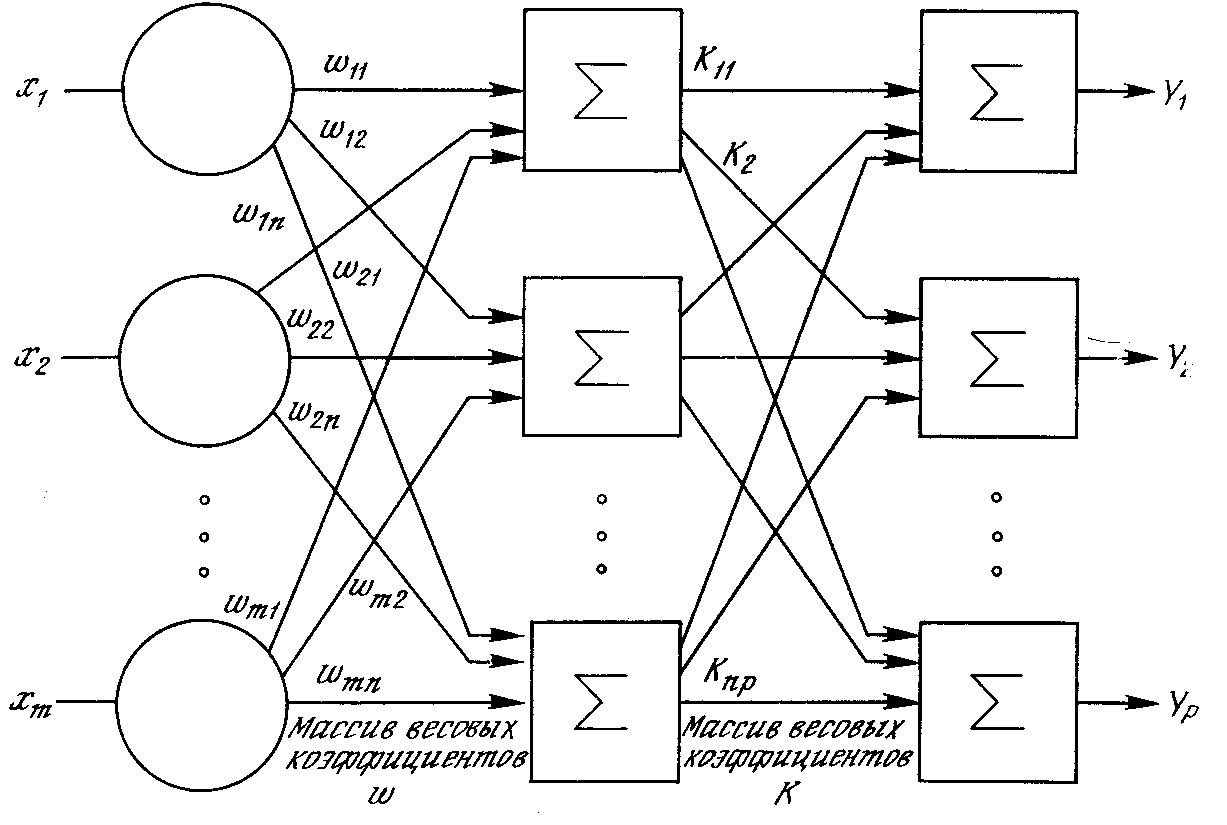
Глубокая нейронная сеть – сеть с большим числом скрытых слоев
Линейная сеть
Линейная модель сети – это сеть без промежуточных слоев, которая в выходном слое содержит только линейные элементы.
Во время работы сеть фактически умножает вектор входов на матрицу весов, а затем к полученному вектору прибавляет вектор смещения (вектор пороговых значений).
Может оказаться так, что задачу, считавшуюся очень сложной, можно успешно не только нейронной сетью, но и простым линейным методом. Если же в задаче не так много обучающих данных, то, вероятно, просто нет оснований использовать более сложные модели.
Структура линейной сети
Линейные сети по своей структуре аналогичны персептрону и отличаются лишь функцией активации.
Выход линейной сети может принимать любое значение, в то время как выход персептрона ограничен значениями 0 или 1.
На рис. * показан линейный нейрон с двумя входами. Он имеет структуру, сходную со структурой персептрона. Единственное отличие состоит в том, что используется линейная функция активации. Весовая матрица W в этом случае имеет только одну строку, и выход сети определяется выражением:
???? = ????(????) = ????(????????+????) =????????+???? = ???????????????????? + ???????????????????? +????
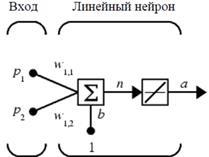
Подобно персептрону, линейная сеть задает в пространстве входов разделяющую линию, на которой функция активации ???? равна 0 (рис. **).
Векторы входа, расположенные выше этой линии, соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. Это означает, что линейная сеть может быть применена для решения задач классификации.
Функция ошибок - это целевая функция, требующая минимизации в процессе управляемого обучения нейронной сети.
С помощью функции ошибок можно оценить качество работы нейронной сети во время обучения.
От качества обучения нейронной сети зависит ее способность решать поставленные перед ней задач
Процесс обучения нейронной сети

Алгоритмы обучения нейронной сети
Обучение с учителем
-
Подготавливается набор обучающих данных. Эти данные представляют собой примеры входных данных и соответствующих им выходов. Сеть учится устанавливать связь между первыми и вторыми; -
Нейронная сеть обучается с помощью того или иного алгоритма управляемого обучения, при котором имеющиеся данные используются для корректировки весов и пороговых значений сети таким образом, чтобы минимизировать ошибку прогноза на обучающем множестве.
Обучение без учителя
-
Обучающие данные содержат только значения входных переменных. -
Сеть учится распознавать внутреннюю структуру данных.
Сбор данных для нейронной сети
Требования к обучающему множеству:
➢Множество не должно содержать всплесков – элементы, свойства которых отличаются от ожидаемых значений;
➢Элементы множества должны быть репрезентативны;
➢Обучающая выборка должна быть в несколько раз больше общего количества
весовых связей в сети;
➢Частные требования.
Выводы:
➢Выбирайте такие переменные, которые, как Вы предполагаете, влияют на результат.
➢С числовыми и номинальными переменными можно работать непосредственно. Переменные других типов следует преобразовать в указанные типы или объявить незначащими.
➢Чем больше в задаче переменных, тем больше нужно иметь наблюдений.
➢ В случае необходимости можно работать с наблюдениями, содержащими пропущенные значения. Если возможно, удалите выбросы. Если данных достаточное количество, уберите из рассмотрения наблюдения с пропущенными значениями.
Подготовка данных для обучения
➢Количество наблюдений в наборе данных. Следует учитывать тот фактор, что чем больше размерность данных, тем больше времени потребуется для обучения сети. ➢Работа с выбросами. Следует определить наличие выбросов и оценить необходимость их присутствия в выборке.
➢Обучающая выборка должна быть представительной (репрезентативной). ➢Обучающая выборка не должна содержать противоречий, так как нейронная сеть однозначно сопоставляет выходные значения входным.
➢Нейронная сеть работает только с числовыми входными данными, поэтому важным этапом при подготовке данных является преобразование и кодирование данных. При использовании на вход нейронной сети следует подавать значения из того диапазона, на котором она обучалась. Например, если при обучении нейронной сети на один из ее входов подавались значения от 0 до 10, то при ее применении на вход следует подавать значения из этого же диапазона или близлежащие.
Существует понятие нормализации данных.
Целью нормализации значений является преобразование данных к виду, который наиболее подходит для обработки, т.е. данные, поступающие на вход, должны иметь числовой тип, а их значения должны быть распределены в определенном диапазоне.
Нормализатор может приводить дискретные данные к набору уникальных индексов либо преобразовывать значения, лежащие в произвольном диапазоне, в конкретный диапазон, например, [0..1].
Нормализация выполняется путем деления каждой компоненты входного вектора на длину вектора, что превращает входной вектор в единичный.
Выбор структуры нейронной сети
Выбор структуры нейронной сети обусловливается спецификой и сложностью решаемой задачи. В большинстве случаев выбор структуры нейронной сети определяется на основе объединения опыта и интуиции разработчика.
Однако существуют основополагающие принципы, которыми следует руководствоваться при разработке новой конфигурации :
➢возможности сети возрастают с увеличением числа ячеек сети, плотности связей между ними и числом выделенных слоев;
➢введение обратных связей наряду с увеличением возможностей сети поднимает вопрос о динамической устойчивости сети;
➢сложность алгоритмов функционирования сети (в том числе, например, введение нескольких типов синапсов - возбуждающих, тормозящих и др.) также способствует усилению мощи НС.
Переобучение нейронной сети
При обучении нейронных сетей часто возникает серьезная трудность, называемая проблемой переобучения
Переобучение - излишне точное соответствие нейронной сети конкретному набору обучающих примеров, при котором сеть теряет способность к обобщению.
возникает в случае слишком долгого обучения, недостаточного числа обучающих примеров или переусложненной структуры нейронной сети.
связано с тем, что выбор обучающего множества является случайным. С первых шагов обучения происходит уменьшение ошибки. На последующих шагах с целью уменьшения ошибки параметры подстраиваются под особенности обучающего множества. Однако при этом происходит "подстройка" не под общие закономерности ряда, а под особенности его части - обучающего подмножества. При этом точность прогноза уменьшается.
Переобучение нейронной сети
Один из вариантов борьбы с переобучением сети - деление обучающей выборки на два множества (обучающее и тестовое).
На первом шаге ошибки прогноза для обучающего и тестового множества одинаковы. На последующих шагах значения обеих ошибок уменьшаются, однако с семидесятого шага ошибка на тестовом множестве начинает возрастать, т.е. начинается процесс переобучения сети.
Сложности применения НС
➢Для построения модели объекта на основе НС требуется выполнение многоцикловой настройки внутренних элементов и связей между ними;
➢ Проблемы, возникающие при подготовке обучающей выборки, связанные с трудностями нахождения достаточного количества обучающих примеров;
➢Обучение сети в ряде случаев приводит к тупиковым ситуациям; ➢Продолжительные временные затраты на выполнение процедуры обучения зачастую не позволяют применять ИНС в системах реального времени;
➢ Поведение обученной ИНС не всегда может быть однозначно предсказуемо, что увеличивает риск применения ИНС для управления дорогостоящими техническими объектами;
➢Обучить и эксплуатировать нейронную сеть для решения многих задач, как правило, может и не специалист, но надежно интерпретировать результаты, а также численно оценивать значимость получаемых прогнозов способны специалисты, имеющие навыки в моделировании нейронных сетей.
Модели нейронных сетей
Персептрон
Большое количество моделей персептрона рассмотрено в основополагающей работе Розенблатта.
Простейшая модель
нейронной сети - однослойный персептрон.
Однослойный персептрон (персептрон Розенблатта) - однослойная нейронная сеть, все нейроны которой имеют жесткую пороговую функцию активации. Однослойный персептрон имеет простой алгоритм обучения и способен решать лишь самые простые задачи.
Классический пример такой нейронной сети - однослойный трехнейронный персептрон.
Перцептрон Розенблатта
Модель Мак-Каллока – Питтса была реализована Фрэнком Розенблаттом: в 1958 г. в виде компьютерной модели (перцептрона), в 1960 г. в виде электронного устройства, распознававшего рукописные изображения некоторых букв и цифр – первого в мире нейрокомпьютера Марк-1.
Однослойный персептрон

Сеть, изображенная на рисунке, имеет ???? входов, на которые поступают сигналы, идущие по синапсам на 3 нейрона. Эти три нейрона образуют единственный слой данной сети и выдают три выходных сигнала.
Алгоритм обучения персептрона


Многослойный персептрон
Многослойный персептрон (MLP) - нейронная сеть прямого распространения сигнала в которой входной сигнал преобразуется в выходной, проходя последовательно через несколько слоев.
В этой модели персептрона должен быть хотя бы один скрытый слой. Присутствие нескольких таких слоев оправдано лишь в случае использования нелинейных функций активации.
Двухслойный перцептрон

Сеть, изображенная на рисунке, имеет n входов. На них поступают сигналы, идущие далее по синапсам на 3 нейрона, которые образуют первый слой. Выходные сигналы первого слоя передаются двум нейронам второго слоя. Последние, в свою очередь, выдают два выходных сигнала.
Многослойных персептрон

Обучение многослойного персептрона
➢Принцип связи между нейронами - "каждый с каждым".
➢Количество нейронов в слоях может быть произвольным.
➢Обычно во всех скрытых слоях одинаковое количество нейронов.
➢Входной слой только распределяет сигналы.
Целью обучения является поиск таких значений весов и порогов сети, которые бы минимизировали ошибку прогноза, выдаваемого сетью.
Функции ошибок:
➢сумма квадратов ошибок; ➢среднеквадратическая ошибка.
Многослойные нейронные сети

Глубокая нейронная сеть – сеть с большим числом скрытых слоев
Линейная сеть
Линейная модель сети – это сеть без промежуточных слоев, которая в выходном слое содержит только линейные элементы.
Во время работы сеть фактически умножает вектор входов на матрицу весов, а затем к полученному вектору прибавляет вектор смещения (вектор пороговых значений).
Может оказаться так, что задачу, считавшуюся очень сложной, можно успешно не только нейронной сетью, но и простым линейным методом. Если же в задаче не так много обучающих данных, то, вероятно, просто нет оснований использовать более сложные модели.
Структура линейной сети
Линейные сети по своей структуре аналогичны персептрону и отличаются лишь функцией активации.
Выход линейной сети может принимать любое значение, в то время как выход персептрона ограничен значениями 0 или 1.
На рис. * показан линейный нейрон с двумя входами. Он имеет структуру, сходную со структурой персептрона. Единственное отличие состоит в том, что используется линейная функция активации. Весовая матрица W в этом случае имеет только одну строку, и выход сети определяется выражением:
???? = ????(????) = ????(????????+????) =????????+???? = ???????????????????? + ???????????????????? +????

Подобно персептрону, линейная сеть задает в пространстве входов разделяющую линию, на которой функция активации ???? равна 0 (рис. **).
Векторы входа, расположенные выше этой линии, соответствуют положительным значениям выхода, а расположенные ниже – отрицательным. Это означает, что линейная сеть может быть применена для решения задач классификации.