Файл: Методические рекомендации по использованию ресурса Работу можно применить при проведении урока по систематизации и закреплении знаний учащихся.docx
Добавлен: 30.11.2023
Просмотров: 108
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Сборник задач по теории вероятностей
(с решениями)
Разработка предназначена дляучащихся 9–11 классов для подготовки к ОГЭ и ЕГЭ по математике.
УМК любой
Цель: показать решение типовых задач по данной теме, закрепить умение учащихся решать данные задачи, подготовить учеников к сдаче ОГЭ и ЕГЭ
Методические рекомендации по использованию ресурса: Работу можно применить:
-
при проведении урока по систематизации и закреплении знаний учащихся -
при проведении консультаций.
Источники информации: Открытый банк ЕГЭ ФИПИ http://fipi.ru/
Теориявероятностей
Классическое определение вероятности
Вероятностью события A называется отношение числа благоприятных для A исходов к числу всех равновозможных исходов:Р(А) =
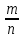
где n — общее число равновозможных исходов, m — число исходов, благоприятствующих событию A.
Противоположные события
Событие, противоположное событию A, обозначают Ā. При проведении испытания всегда происходит ровно одно из двух противоположных событий и
Объединение несовместных событий
Два события A и B называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию A, так и событию B.
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событийA и B:P(AUB)=P(A) + P(B)
Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или непоявления другого события.
Событие C называют пересечением событий A и B (пишут C = A∩B), если событие C означает, что произошли оба события A и B.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей событийA и B:
P(A∩B) = P(A) •P(B)
Формула сложения вероятностей совместных событий:
P(A U B) =P(A) + P(B) – P(A∩B)
1. Из 1000 собранных на заводе телевизоров 5 штук бракованных. Эксперт проверяет один наугад выбранный телевизор из этой 1000. Найдите вероятность того, что проверяемый телевизор окажется бракованным.
Решение.При выборе телевизора наугад возможны 1000 исходов, событию A «выбранный телевизор — бракованный» благоприятны 5 исходов. По определению вероятности P(A) = 5÷1000 = 0,005. Ответ: 0,005.
2.В урне 9 красных, 6 жёлтых и 5 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым? Решение. Общее число исходов равно числу шаров: 9 + 6 + 5 = 20. Число исходов, благоприятствующих данному событию, равно 6. Искомая вероятность равна 6÷20 = 0,3.Ответ: 0,3.
3. Петя, Вика, Катя, Игорь, Антон, Полина бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик.
Решение.Вероятность события равна отношению количества благоприятных случаев к количеству всех случаев. Благоприятными случаями являются 3 случая, когда игру начинает Петя, Игорь или Антон, а количество всех случаев 6. Поэтому искомое отношение равно 3:6=0,5. Ответ: 0,5.
4. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение:Обозначим через А событие «команда России во второй группе». Тогда количество благоприятных событий m = 4 (четыре карточки с номером 2), а общее число равновозможных событий n = 16 (16 карточек) по определению вероятности Р= 4: 16 = 0,25. Ответ:0,25
5.В лыжных гонках участвуют 11 спортсменов из России, 6 спортсменов из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение.Всего спортсменов 11 + 6 + 3 = 20 человек. Поэтому вероятность того, что первым будет стартовать спортсмен не из России равна 9:20 = 0,45. Ответ: 0,45.
Ответ: 0,45
55555 666 6. На каждые 1000 электрических лампочек приходится 5 бракованных. Какова вероятность купить исправную лампочку?
Решение.На каждые 1000 лампочек приходится 5 бракованных, всего их 1005. Вероятность купить исправную лампочку будет равна доле исправных лампочек на каждые 1005 лампочек, то есть 1000:1005=0,995.Ответ: 0,995.
7.В группе туристов 8 человек. С помощью жребия они выбирают шестерых человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?6 : 8=0,75.
Ответ: 0,9478888. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A?
Решение. Каждая команда попадет в группу с вероятностью 0,25. Таким образом, вероятность того, что команда не попадает в группу равна 1-0,25=0,75.Ответ:0,75
9.На турнир по шахматам прибыло 26 участников в том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы.Решение. Всего 26 мест. Пусть Коля займет случайное место в любой группе. Останется 25 мест, из них в другой группе 13. Исходом считаем выбор места для Толи. Благоприятных исходов 13. Р=13/25 = 0,52.Ответ:0,52
10.В классе 16 учащихся, среди них два друга —Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе.Решение.Если Сергею первому досталось некоторое место, то Олегу остаётся 15 мест. Из них 3 — в той же группе, где Сергей. Искомая вероятность равна 3/15.Ответ:0,2
11.В классе 21 учащийся, среди них два друга — Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе. Решение. Пусть один из друзей находится в некоторой группе. Вместе с ним в группе окажутся 6 человек из 20 оставшихся учащихся. Вероятность того, что друг окажется среди этих 6 человек, равна 6 : 20 = 0,3. Ответ: 0,3
12.Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 спортсменов, среди которых 7 участников из России, в том числе Платон Карпов. Найдите вероятность того, что в первом туре Платон Карпов будет играть с каким-либо спортсменом из России?
6:15=0,4. Ответ:0,4.
13. Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 шашистов, среди которых 3 участника из России, в том числе Василий Лукин. Найдите вероятность того, что в первом туре Василий Лукин будет играть с каким-либо шашистом из России?2: 25=0,08. Ответ: 0,08.
14.В классе 26 учащихся, среди них два друга — Сергей и Андрей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Андрей окажутся в одной группе.Ответ 12 : 25 = 0,48.
15. В классе 21 ученик, среди них 2 друга – Тоша и Гоша. На уроке физкультуры класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Тоша и Гоша попали в одну группу.Ответ 6 : 20 = 0,3.
16.В классе 21 учащийся, среди них две подруги - Аня и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Аня и Нина окажутся в одной группе.Ответ: 2: 20 = 0,1.
17.Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали идти. Найдите вероятность того, что часовая стрелка остановилась, достигнув отметки 7, но не дойдя до отметки 1.Ответ. 6 : 12= 0,5 ( 6 делений между 12 и 7, всего 12 делений)
18. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 6, но не дойдя до отметки 9 часов.3:12 = 0,25
При решении задач с монетами число всех возможныхисходов можно посчитать по формуле п=2ª, где α –количество бросков
19. В случайном эксперименте симметричную монету бросают 2раза. Найдите вероятность того, что орел выпадет ровно 1 раз.
Решение.Всего возможны четыре исхода: решка-решка, решка-орёл, орёл-решка, орёл-орёл. Орёл выпадает ровно один раз в двух случаях, поэтому вероятность того, что орёл выпадет ровно один раз равна2:4=0,5. Ответ: 0,5.
20. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу.Ответ: 1:4=0,25
21. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл не выпадет ни разу.
Решение.1:8=0,125Ответ.0,125
22. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно 2 раза.Решение. Составим список возможных вариантов. Бросают 2 раза может выпасть О - Орел, Р - Решка:
ОО, ОР, РО, РР. Всего 4 исхода из них только один случай удовлетворяет условию. Вероятность(P) = 1 / 4 = 0.25. Ответ: 0.25
23. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что решка не выпадет ни разу.Решение. Всего исходов
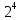 = 16, благоприятных 1 ( ОООО). 1:16 = 0,0625.Ответ: 0,0625
= 16, благоприятных 1 ( ОООО). 1:16 = 0,0625.Ответ: 0,0625При решении задач с кубиками число всех возможныхисходов можно посчитать по формуле п=6ª, где α –количество бросков
24.Определите вероятность того, что при бросании игрального кубика (правильной кости) выпадет нечетное число очков.Решение.При бросании кубика равновозможных шесть различных исходов. Событию "выпадет нечётное число очков" удовлетворяют три случая: когда на кубике выпадает 1, 3 или 5 очков. Поэтому вероятность того, что на кубике выпадет нечётное число очков равна 3:6=0,5. Ответ: 0,5.
25. Определите вероятность того, что при бросании кубика выпало число очков, не большее 3.
Решение.При бросании кубика равновозможны шесть различных исходов. Событию "выпадет не больше трёх очков" удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет не больше трёх очков равна 3:6=0,5 Ответ: 0,5.Ответ: 0,5Ответ: 0,5
26. 27 22 Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
Решение.При бросании кубика 6²= 36 различных исходов. Событию "выпадет больше трёх очков" удовлетворяют три случая: когда на кубике выпадает 4, 5, или 6 очков , благоприятных исходов 9 (4,4; 4,5; 4,6; 5,4; 5,5; 5,6; 6,4; 6,5; 6,6.) Ответ:9: 36 = 0,25.
27. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.Решение.При бросании кубика 6³= 216 различных исходов, благоприятных