МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИБАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ»  им. Д.Ф. УСТИНОВА Кафедра системы приводов, мехатроника и робототехника (И8)Дисциплина «Теория машин и механизмов»Лабораторная работа № 1СТРУКТУРНЫЙ И КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКОГО МЕХАНИЗМА

Выполнил студент		Яшков А.Р.
Фамилия И.О.
группа	Е202Б
Преподаватель		Ельчинский В. С.
		Фамилия И. О.
		Подпись преподавателя		Дата
Допуск
Выполнение
Защита

Санкт-Петербург2022 г.

1. 
   СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА
   

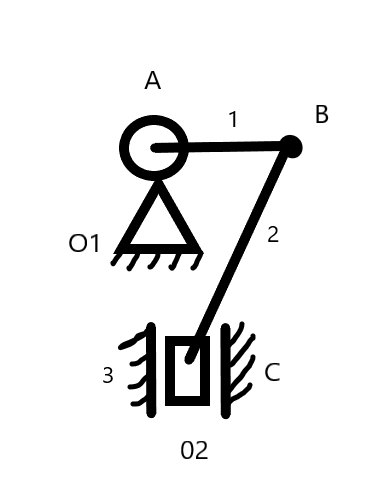
На рисунке представлена схема исследуемого четырёхзвенный рычажного механизма с тремя подвижными звеньями.Число степеней свободы по формуле Чебышева для плоских механизмовW=3n-2p₅-p₄=3*3-2*4=1.где n – количество подвижных звеньев, p₅ и p₄ –количество кинематических пар 5-го и 4-го класса соответственно.2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМАКинематический анализ производится экспериментально-аналитически.Функцию S(ϕ₁

---

) положения ползуна 3 в зависимости от угла поворота кривошипа 1 получаем экспериментально в виде таблицы с шагом 10^о по углу поворота кривошипа. Результаты эксперимента представлены в таблице 1.1.

Таблица 1.1

i	ϕ1o		Si, м	i	ϕ1o		Si, м	i	ϕ1o	S, м	Si, м
0	0		0	13	130		0.072	26	260		0.061
1	10		0.007	14	140		0.076	27	270		0.056
2	20		0.01	15	150		0.079	28	280		0.049
3	30		0.012	16	160		0.081	29	290		0.041
4	40		0.017	17	170		0.083	30	300		0.035
5	50		0.023	18	180		0.084	31	310		0.028
6	60		0.03	19	190		0.083	32	320		0.022
7	70		0.035	20	200		0.082	33	330		0.015
8	80		0.042	21	210		0.081	34	340		0.010
9	90		0.05	22	220		0.079	35	350		0.006
10	100		0.056	23	230		0.075	36	360		0
11	110		0.061	24	240		0.071
12	120		0.066	25	250		0.067

---

Полагая, что кривошип вращается с постоянной угловой скоростью ω₁=29c^-1 , следовательно, ϕ₁=ω₁t, получим функцию положения от времени S(t). Для этого вычислим шаг таблицы по времени: Δt = Δϕ₁ рад /ω₁ = 0,17453/29 = 0,006018 с, где Δϕ₁ рад = Δϕ₁°/180 = 10/180 = 0,17453 рад.Для аналитической обработки функции S(t) проведем ее аппроксимацию и фильтрацию пятью методами. Обработку данных эксперимента проведем с помощью программы ApproxFSP.exe.6.0. 3. Аппроксимация функции положения тригонометрическим рядом Фурье.В этом случае функцию S(t) разлагаем в тригонометрический ряд Фурье и дифференцированием ряда определяем зависимости скорости v(t) и ускорения а(t) ползуна. При этом необходимо решить вопрос об оптимальном числе членов ряда. Разложение функции в такой ряд означает её приближенную замену тригонометрическим полиномом, являющимся суммой ряда:S_ф(t)= 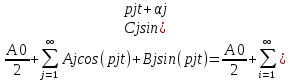)где A_j , B_j – коэффициенты ряда, p_j = 2πj/T – частоты, по которым производится разложение, T = 2π/ω₁=2π/28 = 0.224 с – время полного оборота кривошипа C_j– амплитуда j-й гармоники, _j – её фаза, m – число членов ряда. В данном случае функция S(t) задана таблицей значений в конечном числе точек n = 36, поэтому максимальное число членов ряда m_max = n/2 = 36/2 = 18. На первом этапе разложим S(t) в ряд с максимально возможным числом членов m = 18. Результаты представлены на рис.1 и в табл.1. 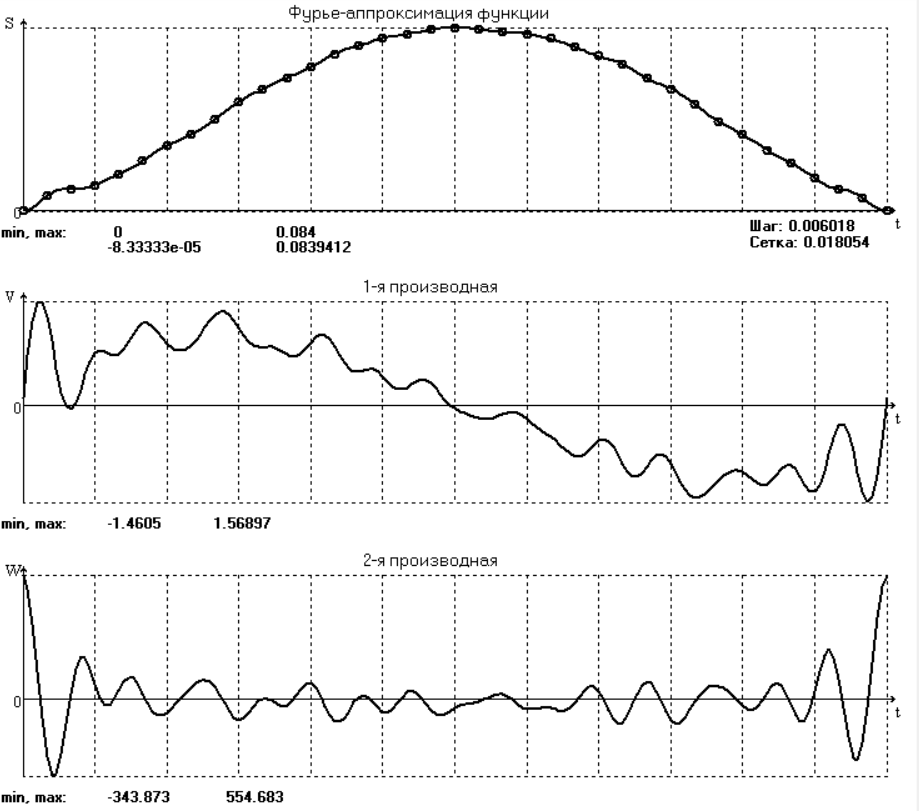В этом случае значения ряда Фурье в узлах практически совпадают с данными эксперимента.На графике скорости и особенно ускорения явно видны паразитные осцилляции, вызванные погрешностями работы механизма и погрешностями замера значений S(t). 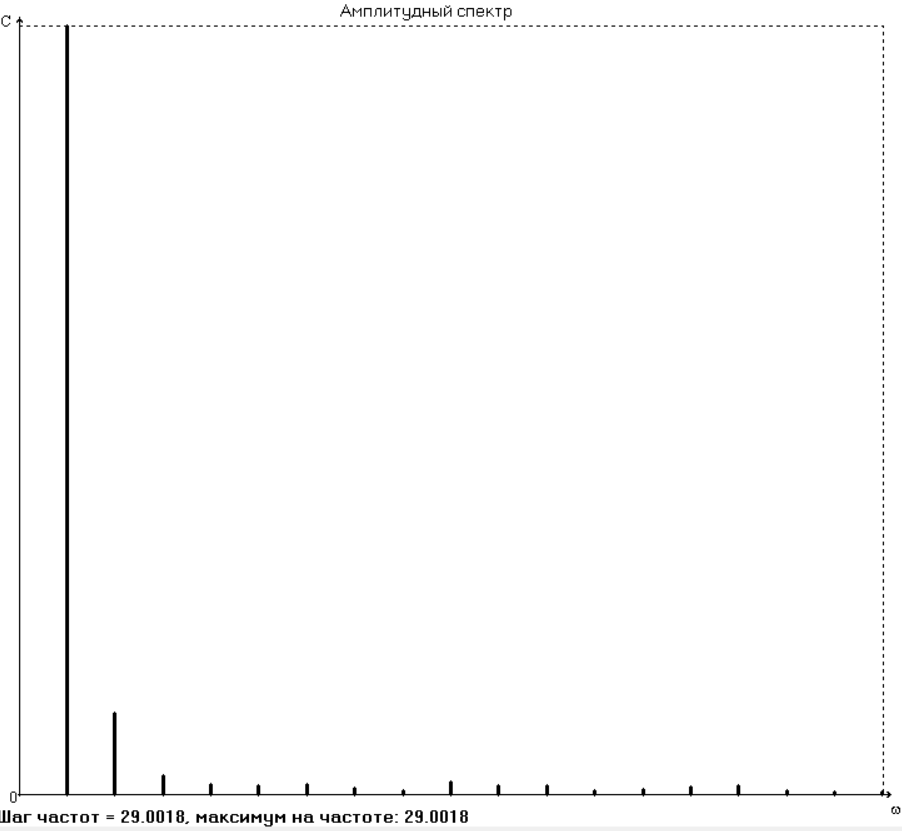Во многих случаях возникает потребность сглаживания такого рода зависимостей.Оценим значимость членов ряда с помощью амплитудного спектра, показанного на рис.2 и в табл.2.АналÐ

---

Смотрите также файлы

• Развитие социального аспекта в воспитании в xviii xix вв.docx

• самарский энергетический колледж (гбпоу сэк ) дневник учебной практики (УП.) Специальность 13. 02. 02 Теплоснабжение и теплотехническое оборудование Студент(ки) гр..docx

• Лабораторная работа 2 структурный и кинематический анализ и синтез плоских кулачковых механизмов.docx

• Проверяемая цель.docx

• Лекция Учение о половом цикле. План лекции.pdf