МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

БАЛТИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ВОЕНМЕХ»  им. Д.Ф. УСТИНОВА 

Кафедра системы приводов, мехатроника и робототехника (И8)



Лабораторная работа №2

СТРУКТУРНЫЙ

И КИНЕМАТИЧЕСКИЙ АНАЛИЗ

И СИНТЕЗ ПЛОСКИХ

КУЛАЧКОВЫХ МЕХАНИЗМОВ

Выполнила студент		Яшков А.Р..
Фамилия И.О.
группа	Е202Б
Преподаватель		Ельчинский В. С.
		Фамилия И. О.
		Подпись преподавателя		Дата
Допуск
Выполнение
Защита

Санкт-Петербург

2022 г

Структурный анализ механизма

Исследуется плоский кулачковый механизм с вращающимся кулачком, прямолинейно движущимся толкателем, с силовым замыканием, с роликовым контактом между кулачком и толкателем. Его структурная схема представлена на картинке, где 1 – кулачок, 2 – толкатель, 3 – стойка, 4 – ролик


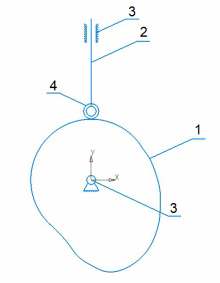
Звенья этого механизма образуют три кинематические пары:

1) кулачок со стойкой – плоский шарнир 5-го класса;

2) толкатель со стойкой – поступательная кинематическая пара

5-го класса;

3) кулачок с толкателем – кинематическая пара 4-го класса.

Число степеней свободы по формуле Чебышева для плоских механизмов определяется по схеме на рис. 2.1,б:

---

W = 3n – 2p5 – p4 = 3⋅2 – 2⋅2 – 1 = 1,

где n – количество подвижных звеньев, p5 и p4 – количество кинематических пар 5-го и 4-го класса соответственно
2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМА

Кинематический анализ производится экспериментально-аналитически. Функцию S(φ1) положения толкателя 2 в зависимости от угла поворота кулачка 1 получаем экспериментально в виде таблицы с шагом 10° по углу поворота кулачка. Результаты эксперимента представлены в таблице

i	ᵠ	S(м)	i	ᵠ	S(м)
0	0	0	19	190	0,025
1	10	0,002	20	200	0,025
2	20	0,004	21	210	0,025
3	30	0,009	22	220	0,025
4	40	0,014	23	230	0,025
5	50	0,019	24	240	0,025
6	60	0,023	25	250	0,025
7	70	0,024	26	260	0,025
8	80	0.025	27	270	0,024
9	90	0.025	28	280	0,023
10	100	0.025	29	290	0,021
11	110	0.025	30	300	0,018
12	120	0.025	31	310	0,013
13	130	0.025	32	320	0,010
14	140	0.025	33	330	0,008
15	150	0.026	34	340	0,007
16	160	0,028	35	350	0,003
17	170	0,025	36	360	0
18	180	0,025

---

Полагая, что кулачок вращается с постоянной угловой скоростью ω1 = 23 рад/с, следовательно, φ1 = ω1*t, получаем функцию положения от времени S(t). Δϕ1 рад = Δϕ1°/180 = 10/180 = 0,17453 рад. Вычислим шаг таблицы по времени: : Δt = Δϕ1 рад /ω1 = 0,17453/23 = 0,007588 с. Для аналитической обработки функции S(t) проводим её аппроксимацию и фильтрацию пятью методами. Обработку данных эксперимента выполним с помощью программы ApproxFSP.exe

3.1. Аппроксимация функции положения

тригонометрическим рядом Фурье

В этом случае функцию S(t) разлагаем в ряд Фурье и дифференцированием ряда определяем зависимость скорости v(t) и ускорения а(t)

ползуна. При этом необходимо решить вопрос об оптимальном числе

членов ряда. Разложение функции в ряд Фурье означает её приближенную замену тригонометрическим полиномом, являющимся суммой ряда



где Aj, Bj – коэффициенты ряда, pj = 2π j/T– частоты, по которым производится разложение, T =2π/ω1 = 2π/23 = 0,27 с – время полного

оборота кулачка; 2 2 Cj = (Aj + Bj)^(1/2) – амплитуда j-й гармоники, αj – её

фаза, m – число членов ряда.

В данном случае функция S(t) задана таблицей значений в конечном числе точек n = 36, поэтому максимальное число членов ряда

mmax = n/2 = 36/2 = 18.

Формулы для вычисления коэффициентов ряда Фурье при табличном задании функции [2]:



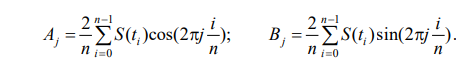
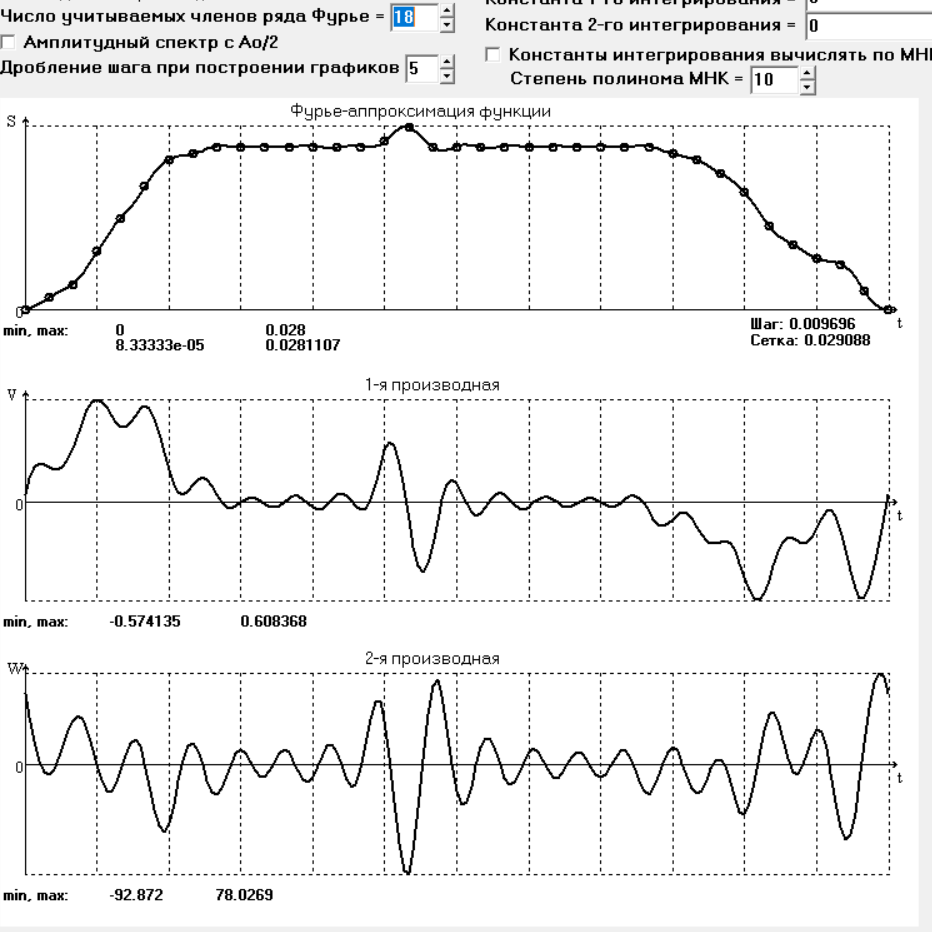
На первом этапе разложим S(t) в ряд с максимально возможным

числом членов m = 18. Результаты представлены на рис. 3.1 и в

табл. 3.2. В этом случае значения ряда Фурье в узлах близки к данным

эксперимента, но в промежутках между узлами наблюдаются волнообразные отклонения, особенно заметные на графиках производных.

В частности, на фазах ближнего и дальнего выстоя скорость и ускорение должны быть равны нулю, а аппроксимирующая функция осциллирует. Во многих случаях возникает потребность в сглаживании

такого рода зависимостей.




Оценим значимость членов ряда с помощью амплитудного спектра функции,

---

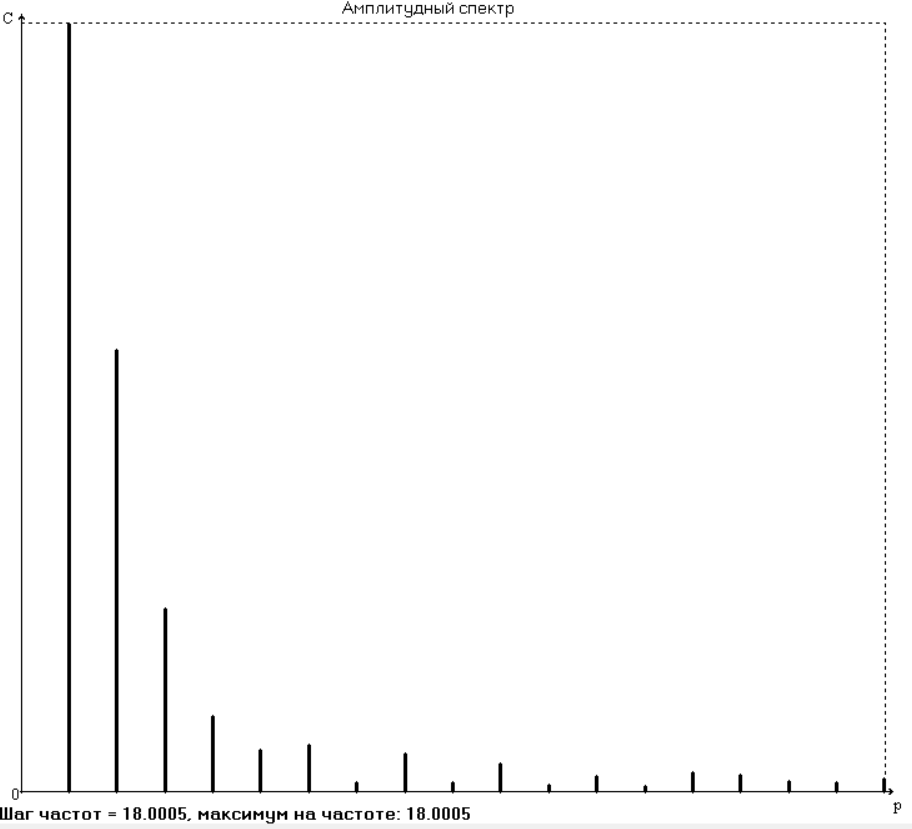
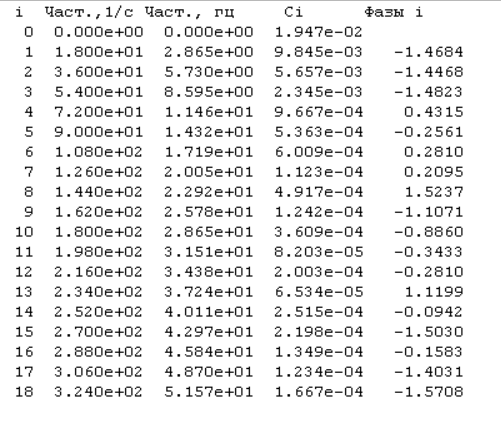
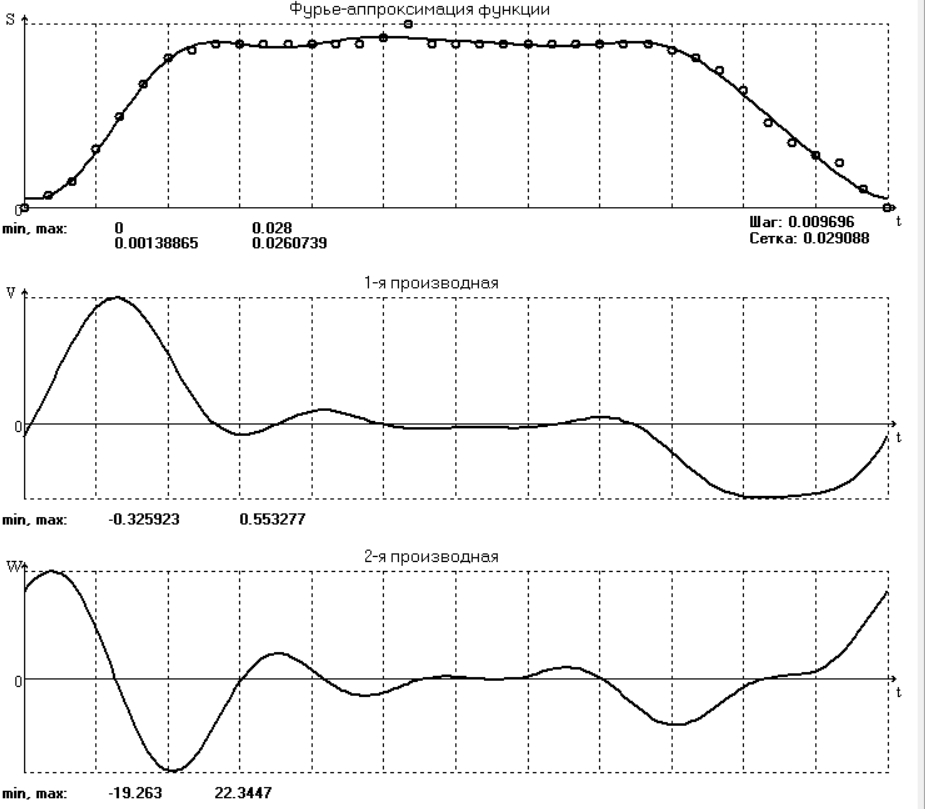
Анализ амплитудного спектра исследуемой функции показывает, что основными частотами, присутствующими в ней, являются первые шесть, однако исследования, проведённые с помощью программы ApproxFSP, показали, что наилучшая аппроксимация получается при учете первых десяти частот. Результаты представлены на рис. 3.3 и в табл. 3.4. Функция аппроксимирована удовлетворительно на всем участке. Первая производная (скорость толкателя) удовлетворительно аппроксимирована на фазах удаления и возврата, на фазах выстоя заметны погрешности. Вторая производная (ускорения толкателя) аппроксимирована неудовлетворительно. Аппроксимирующее выражение (3.1) для данной функции с учетом первых пяти членов ряда приобретает вид

SФ(t) = 0,01947 + 0,009845 sin(18t -1,4684) + 0,005657 sin(36t -1,4468) + 0,002345 sin(54t +0,0435) + 0,0009667 sin(72t -0,2561) + 0,0005363 sin(90t +0.2810)



3.2. Фильтрация функции с помощью скользящих средних

Скользящие средние являются одним из простейших цифровых

фильтров. Сглаженная (отфильтрованная) функция получается путём

вычисления средних арифметических значений по указанному числу

точек. При этом первые и последние точки в таблице отфильтрованной функции сохраняют свои значения.

В данном исследовании функция задана в 36 точках: S0, S1, S2,…S36.

Далее мы строим скользящие средние по трем точкам, и отфильтрованными значениями функции будут:

Sф0 = S0;

Sф1 = (S0 + S1 + S2)/3;

Sф2 = (S1 + S2 + S3)/3;

…

Sф35 = (S34 + S35 + S36)/3;

Sф36 = S36.

Исследования, проведенные с помощью программы ApproxFSP,

показали, что увеличение числа точек, по которым вычисляются

средние, приводит к увеличению погрешности аппроксимации самой

функции на фазе дальнего выстоя, а существенного улучшения сглаживания на фазах удаления и возврата при этом не происходит. Оптимальным в данном случае можно признать сглаживание по трём точкам.



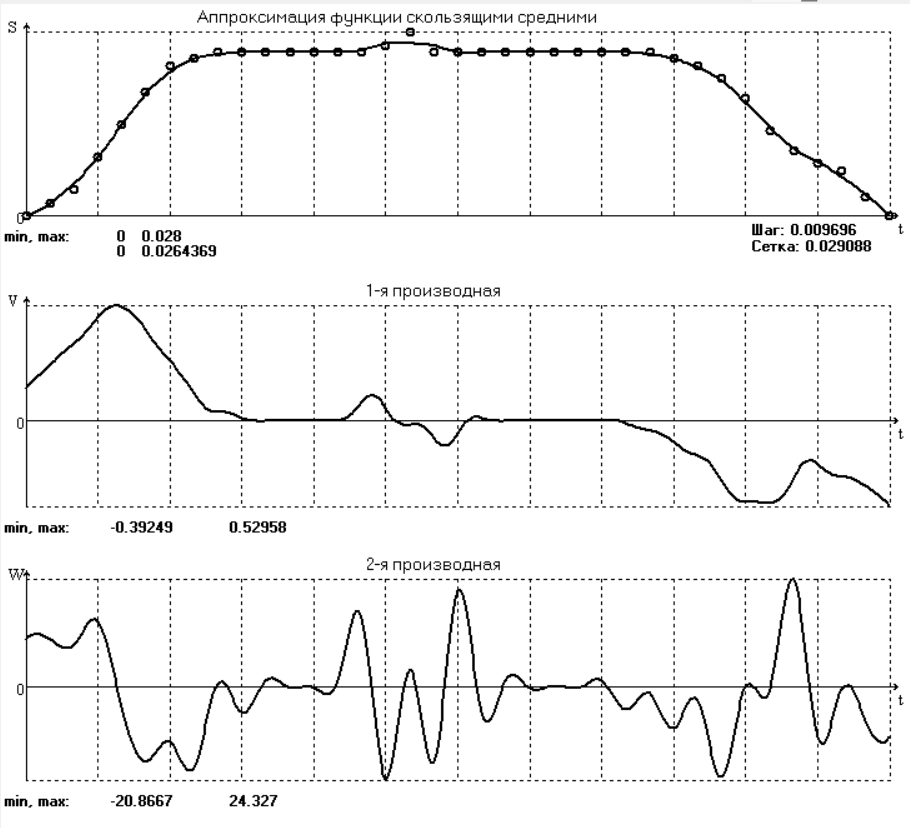
Оценим качество фильтрации. Функция аппроксимирована удовлетворительно, со сглаживанием. Первая производная аппроксимирована в целом удовлетворительно за исключением начала фазы удаления. Вторая производная сглажена неудовлетворительно. Кроме того, на графиках производных начальное значения не равно конечному, в то время как в данном случае они должны быть

---

равны по физическому смыслу этих функций





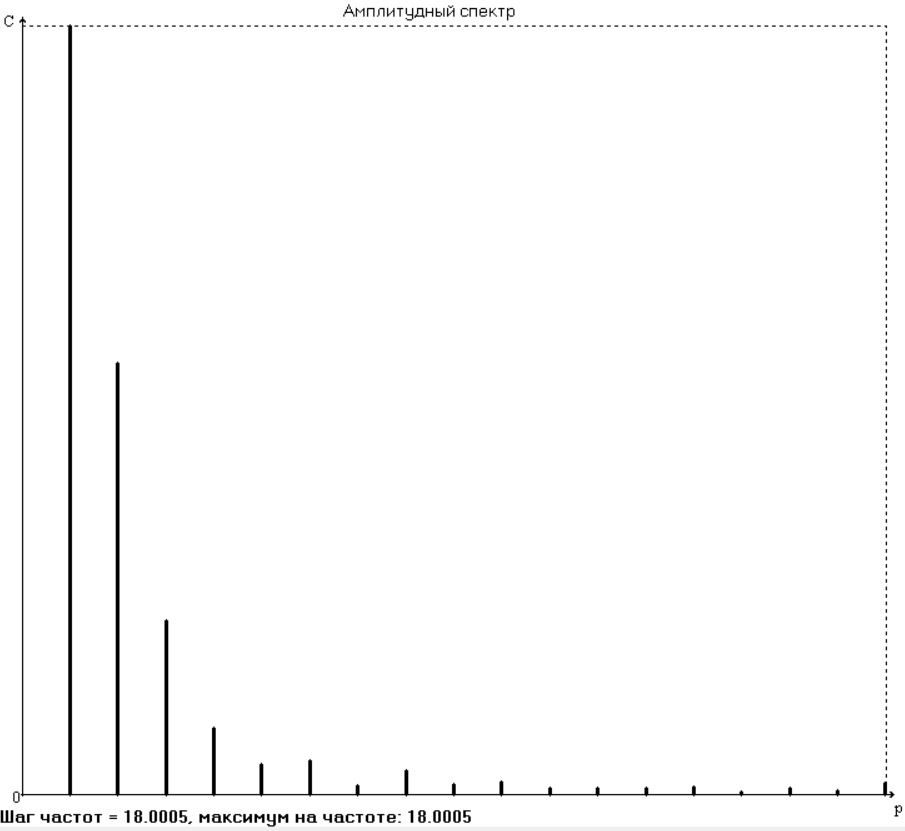
3.3. Применение интерполяционного сплайна

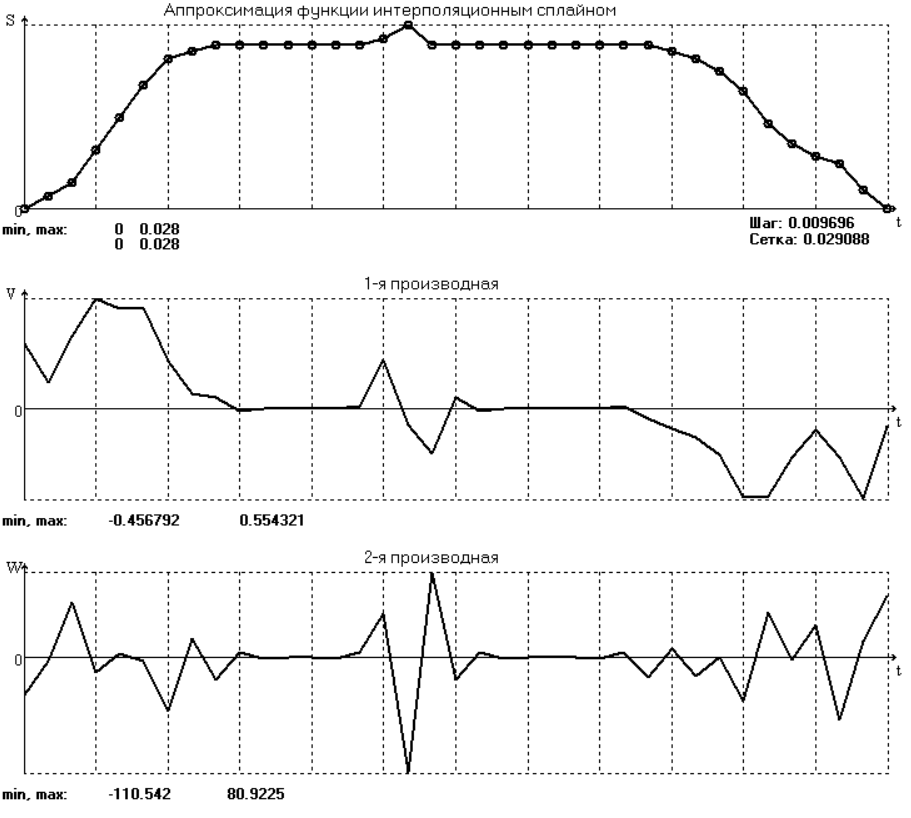
Интерполяционный кубический сплайн – это совокупность полиномов третьей степени: SСi(t) = Si + bi(t – ti) + ci(t – ti) 2 + di(t – ti) 3 , (3.3) где Si – значения аппроксимируемой функции в узлах, ti – значения аргумента в узлах, 푏푖, 푐푖, 푑푖 – коэффициенты сплайна для i-го участка, i = 0,1,2, … n–1– номер участка, n – число точек в таблице, считая с нуля. Построение такого сплайна состоит в определении коэффициентов bi, ci, di. Тогда для каждого i-го участка по формуле (3.3) можно найти значение сплайна SСi(t) для любого ti ≤ t ≤ ti+1, которое и будет приближённым значением функции S(t). Алгоритм построения сплайна вида (3.3) описан в работах [4, 5]. Дифференцированием аппроксимирующей функции (3.3) определяется скорость звена: v(t) ≈ vСi(t) = bi + 2ci(t – ti)+ 3di(t – ti) 2 , (3.4) в частности, значения производной в узлах v(t) ≈ bi . Результаты аппроксимации представлены на рис. 3.5 и в табл. 3.6. Как и следует из названия, этот сплайн дает интерполирующую аппроксимацию. Операция сглаживания с его помощью невозможна. Этот метод целесообразно применять в тех случаях, когда аппроксимирующую функцию надо проводить в точности по исходным точкам. Здесь на графиках производных также наблюдается неравенство значений производных в крайних точках.





3.4. Применение сглаживающего сплайна

Для построения сглаживающего сплайна формируется так называемый “коридор” (рис. 3.6), т.е. для каждой точки задается максимально и минимально допустимое значение функции, а сам сплайн строится так, чтобы его график проходил между точками этого коридора, минимизируя энергию изгиба. Коридор, показанный на рис. 3.6, сформирован так, чтобы “закрепить” начальную точку и точки на фазах дальнего и ближнего выстоя. Результаты показаны на рис. 3.7 и в табл. 3.7. Функция аппроксимирована удовлетворительно, со сглаживанием. Однако на графиках производных проявляется основной недостаток – неравенство начального и конечного значений, в то время как функция в данном случае периодична по своей сути.

---

Смотрите также файлы

• Проверяемая цель.docx

• Лекция Учение о половом цикле. План лекции.pdf

• Тоо казахалтын филиал рудник жолымбет.docx

• Практическая работа к разделу 1 Ценности.docx

• Удк 34 doi 10. 34670AR. 2020. 32. 82. 001.pdf