Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Ивановский государственный политехнический университет»

Институт заочного образования

Кафедра инженерной и компьютерной графики

Контрольная работа

По дисциплине «Основа научных исследований»

Тема: «Одно-, двух- и многофакторный дисперсионный анализ»

Выполнил:

Волков Д.Н.

Группа: ПТМ-51з

Шифр: 186097

Проверил:

Алешин Р.Р.

Иваново 2023

СОДЕРЖАНИЕ

Введение...............................................................................................................................3

1. Однофакторный дисперсионный анализ.......................................................................4

2. Двухфакторный дисперсионный анализ.......................................................................4

2. Многофакторный дисперсионный анализ.....................................................................5

Список литературы..............................................................................................................6

ВВЕДЕНИЕ

Дисперсионный анализ (от латинского Dispersio – рассеивание) – статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Метод был разработан биологом Р. Фишером в 1925 году и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость дисперсионного анализа для экспериментов в психологии, педагогике, медицине и др.

Целью дисперсионного анализа является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.

1. ОДНОФАКТОРНЫЙ ДИСПЕРСИОННЫЙ АНАЛИЗ

Задачей дисперсионного анализа является изучение влияния одного или нескольких факторов на рассматриваемый признак.

Однофакторный дисперсионный анализ используется в тех случаях, когда есть в распоряжении три или более независимые выборки, полученные из одной генеральной совокупности путем

---

изменения какого-либо независимого фактора, для которого по каким-либо причинам нет количественных измерений.

Для этих выборок предполагают, что они имеют разные выборочные средние и одинаковые выборочные дисперсии. если выборки принадлежат одной и той же генеральной совокупности, то разброс данных между выборками (между группами) должен быть не больше, чем разброс данных внутри этих выборок (внутри групп).

С помощью однофакторного дисперсионного анализа можно найти ответы, например, на следующие вопросы:

1. 
   Действительно ли различаются предпочтения потребителей к торговой марке в зависимости от их уровня дохода;
   
2. 
   Действительно ли различаются предпочтения потребителей к торговой марке в зависимости от вида рекламного ролика, который они посмотрели;
   
3. 
   Различаются ли группы потребителей по предпочтениям мест приобретения товара;
   
4. 
   Влияет ли уровень образования респондентов на выбор мета отдыха;
   
5. 
   Различаются ли географические сегменты по товарным предпочтениям потребителей.
   

Последовательность проведения однофакторного дисперсионного анализа:

1. 
   Формулировка вопроса в соответствии с требованиями, предъявляемыми к переменным, выбор зависимой и независимой переменных.
   
2. 
   Формулирование исходной (нулевой гипотезы), согласно которой нет связи между выбранными переменными. В результате анализа нулевая гипотеза должна быть подтверждена или опровергнута.
   
3. 
   В ходе проведения анализа проверяются условия равенства дисперсий зависимой переменной в нескольких выбранных группах (категориях).
   
4. 
   Проведение проверки неравенства средних значений зависимой переменной в сравниваемых группах для выявления взаимосвязи между переменными.
   
5. 
   Определение особенностей выявленной взаимосвязи, выявление категорий ее обуславливающих.
   

Пример. Изделие железнодорожного транспорта с целью испытания на надежность эксплуатируется q раз, i=1,...q на p уровнях времени работы Tj , j=1,..., p. В каждом испытании подсчитываются числа отказов n_ij. На уровне значимости α = 0,05 исследовать влияние времени работы изделия на число появления отказов методом однофакторного дисперсионного анализа при q=4, p=4. Результаты испытаний n

---

_ij представлены в таблицах.
Решение.
Процедура однофакторного дисперсионного анализа. Находим групповые средние:

N	П1	П2	П3	П4
1	145	210	195	155
2	140	200	190	150
3	150	190	240	180
4	190	195	210	175
x	156.25	198.75	208.75	165

Обозначим р - количество уровней фактора (р=4). Число измерений на каждом уровне одинаково и равно q=4.
В последней строке помещены групповые средние для каждого уровня фактора.
Общую среднюю можно получить как среднее арифметическое групповых средних:
 (1)
На разброс групповых средних процента отказа относительно общей средней влияют как изменения уровня рассматриваемого фактора, так и случайные факторы.
Для того чтобы учесть влияние данного фактора, общая выборочная дисперсия разбивается на две части, первая из которых называется факторной S²_ф, а вторая - остаточной S²_ост.
С целью учета этих составляющих вначале рассчитывается общая сумма квадратов отклонений вариант от общей средней:
R_общ =∑∑(x_ij-x) (2)
и факторная сумма квадратов отклонений групповых средних от общей средней, которая и характеризует влияние данного фактора:

---

R_ф =q·(x_ij-x)
Последнее выражение получено путем замены каждой варианты в выражении R_общ групповой средней для данного фактора.
Остаточная сумма квадратов отклонений получается как разность:
R_ост =R_общ -R_ф
Для определения общей выборочной дисперсии необходимо R_общ разделить на числоизмерений pq:

а для получения несмещенной общей выборочной дисперсии это выражение нужно умножить на pq/(pq-1):

Соответственно, для несмещенной факторной выборочной дисперсии:

где p-1 - число степеней свободы несмещенной факторной выборочной дисперсии.
С целью оценки влияния фактора на изменения рассматриваемого параметра рассчитывается величина:

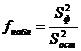
Так как отношение двух выборочных дисперсий S²_ф и S²_ост распределено по закону Фишера-Снедекора, то полученное значение f_набл сравнивают со значением функции распределения

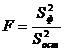
в критической точке f_кр, соответствующей выбранному уровню значимости a.
Если f_набл>f_кр, то фактор оказывает существенное воздействие и его следует учитывать, в противном случае он оказывает незначительное влияние, которым можно пренебречь.
Для расчета R_набл и R_ф могут быть использованы также формулы:
 (4)

---

Находим общую среднюю по формуле (1):
Для расчета Rобщ по формуле (4) составляем таблицу 2 квадратов вариант:

N	П21	П22	П23	П24
1	21025	44100	38025	24025
2	19600	40000	36100	22500
3	22500	36100	57600	32400
4	36100	38025	44100	30625
∑	99225	158225	175825	109550

Общая средняя вычисляется по формуле (1):

R_общ = 99225 + 158225 + 175825 + 109550 - 4 • 4 • 182.19² = 11748.44
Находим R_ф по формуле (5):
R_ф = 4(156.25² + 198.75² + 208.75² + 165²) - 4 • 182.19² = 7792.19
Получаем R_ост: R_ост = R_общ - R_ф = 11748.44 - 7792.19 = 3956.25
Определяем факторную и остаточную дисперсии:



Если средние значения случайной величины, вычисленные по отдельным выборкам одинаковы, то оценки факторной и остаточной дисперсий являются несмещенными оценками генеральной дисперсии и различаются несущественно.
Тогда сопоставление оценок этих дисперсий по критерию Фишера должно показать, что нулевую гипотезу о равенстве факторной и остаточной дисперсий отвергнуть нет оснований.

---

Смотрите также файлы

• Взаимодействие цветов и эмоций.docx

• МЖиг мт212 Кумвенда Кумбукани.docx

• Контрольные вопросы для самостоятельной подготовки по теме семинарского занятия 2 Послевоенный мир в условиях холодной войны (1946 1964 гг.).docx

• Докладов по теме Основы конституционного права рф.docx

• Теория культуры учебное пособие пенза ииц пгу 2012 3 содержание предисловие тема введение в культурологию.pdf