Файл: Решение Исходя из второго закона Ньютона импульс силы равен изменению количества движения, имеем выражение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 34
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача №1
На тело массой m, движущееся со скоростью V0, начинает действовать сила F(t) в течении времени от t1 до t2. Чему равна скорость тела по окончанию действия силы?
| Дано: 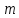 =1,6 кг. =1,6 кг.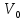 = 4 м/c. = 4 м/c.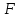 = 2+2t Н. = 2+2t Н.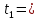 2 с. 2 с.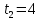 c. c. |
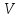 – ? – ? |
Исходя из второго закона Ньютона – импульс силы равен изменению количества движения, имеем выражение:
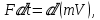
так как по условиям задачи изменению подвергается скорость, а масса остаётся неизменной, выражение принимает вид:
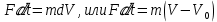
Определим величину действующей силы:
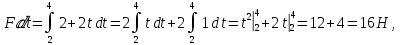
таким образом:
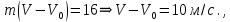
подставляя значение начальной скорости в полученное выражение, определяем скорость по окончанию действия силы:
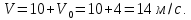
Ответ: скорость тела по окончанию действия силы равна 14 м/с.
Задача №2
Определить величину силы, действующей на тело, в точке с координатами
 по заданной зависимости потенциальной энергии от координат
по заданной зависимости потенциальной энергии от координат 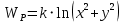 .
.| Дано: 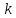 = 4 = 4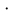 10-5 Н 10-5 Н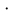 м2. м2.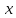 = 40 cм. = 40 cм.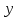 = 30 см. = 30 см. |
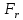 – ? – ? |
Решение:
Потенциальная энергия в общем случае является функцией координат, в данном случае:
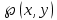 и ее дифференциал имеет вид:
и ее дифференциал имеет вид: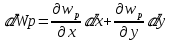
Исходя из равенства
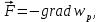 имеем:
имеем: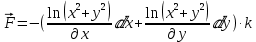
Определим частные производные:
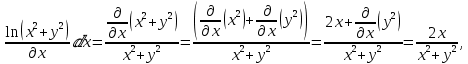
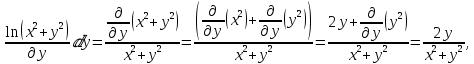
Далее, находим градиент в точке
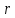 :
: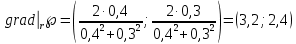
Определим модуль градиента:
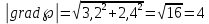
Таким образом сила, действующая на тело равна:
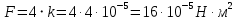
Ответ: величина силы, действующей на тело, в точке (40;30) равна 16
 10-5 Н
10-5 Н м2.
м2.Задача №2
С наклонной плоскости высотой h скатывается сплошной цилиндр. Чему равна скорость цилиндра у основания наклонной плоскости. Трение и проскальзывание цилиндра во время движения отсутствуют.
| Дано: 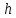 = 2,4 м. = 2,4 м. |
 – ? – ? |
Для решения задачи применим закон сохранения энергии. Потенциальная энергия
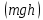 переходит в кинетическую энергию, которая состоит из энергии поступательного движения
переходит в кинетическую энергию, которая состоит из энергии поступательного движения 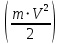 и энергии вращательного движения
и энергии вращательного движения 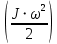 :
: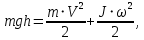
подставив в данное выражение формулы угловой скорости
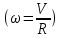 и момента инерции сплошного цилиндра
и момента инерции сплошного цилиндра
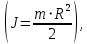 определим скорость движения цилиндра в конце наклонной плоскости:
определим скорость движения цилиндра в конце наклонной плоскости: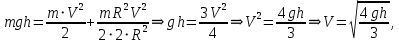
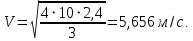
Ответ: скорость цилиндра у основания наклонной плоскости составила 5,656 м/с.