ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Интерференция света
1.1. Список основных формул
Оптическая длина пути L световой волны:
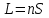 , (4.1)
, (4.1)где S – расстояние, пройденное волной в среде с показателем преломления n.
Оптическая разность хода
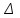 двух волн:
двух волн: (4.2)
(4.2)Условие максимума интенсивности света при интерференции:
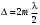 , (4.3)
, (4.3)где – длина световой волны.
Условие минимума интенсивности света при интерференции:
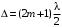 . (4.4)
. (4.4)При решении задач на интерференцию необходимо учитывать, что при отражении луча от оптически более плотной среды происходит изменение фазы светового вектора на . Это приводит к появлению в разности хода двух лучей добавочного слагаемого
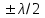 .
. Ширина интерференционной полосы x в опыте Юнга:
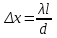 , (4.5)
, (4.5)где d – расстояние между источниками света, l– расстояние от источников до экрана.
Оптическая разность хода лучей отраженных от верхней и нижней грани тонкой пленки (пластинки), находящейся в воздухе определяется выражением:
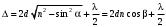 , (4.6)
, (4.6)где d – толщина пленки (пластинки), n– ее показатель преломления, и – углы падения и преломления, соответственно.
Радиусы темных колец Ньютона в отраженном свете:
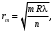 (4.7)
(4.7)где n – показатель преломления вещества клина (зазора между линзой и пластинкой), в случае воздушного слоя n=1, R – радиус кривизны линзы, m – номер кольца.
Радиусы светлых колец Ньютона в отраженном свете:
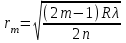 . (4.8)
. (4.8)При наблюдении колец Ньютона в проходящем свете, по формуле (4.7) рассчитываются радиусы светлых колец, а по формуле (4.8) – темных.
«Дифракция света»
1.1. Список основных формул
Радиус rm зоны Френеля с номером m,в случае точечного источника света, рассчитывается по формуле:
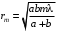 . (1.1)
. (1.1)где a – расстояние от источника света до фронта волны, b – расстояние от волнового фронта до точки наблюдения.
В случае плоской волны, радиус зоны Френеля с номером m может быть выражен:
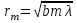 . (1.2)
. (1.2)При дифракции света на щели условия дифракционных минимумов и максимумов записываются, соответственно:
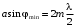 , (1.3)
, (1.3) ,(1.4)
,(1.4)где a – ширина щели, m– порядок дифракционного минимума (максимума),
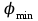 и
и 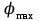 – углы, под которыми наблюдаются дифракционные минимумы и максимумы, соответственно.
– углы, под которыми наблюдаются дифракционные минимумы и максимумы, соответственно.При дифракции света на дифракционной решетке, углы дифракции, под которыми будут наблюдаться главные максимумы, определяются выражением
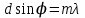 , (1.5)
, (1.5)где m = 0, 1, 2...– порядок главного максимума, d – постоянная (период) решетки.
Период решетки d связан с числом штрихов n, приходящихся на единицу длины решетки, соотношением
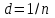 . (1.6)
. (1.6)Общее число N главных максимумов, которые может дать дифракционная решетка, равно
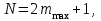 (1.7)
(1.7)где
 – наибольший порядок максимума, наблюдаемого по одну сторону от центрального (
– наибольший порядок максимума, наблюдаемого по одну сторону от центрального (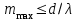 ).
).