Файл: Курсовая работа по дисциплине Нормирование точности в конструкторскотехнологических процессах.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Курсовая работа

Дисциплина: Не указана

Добавлен: 30.11.2023

Просмотров: 66

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


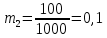
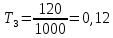
  1. Произведем проверку правильности назначения допусков соответствующих размеров по уравнению:



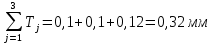
Полученная сумма допусков превышает заданный допуск замыкающего размера на величину равную 0,01 что составляет приблизительно 1% от ТΔ.

  1. Осуществим увязку средний отклонений для чего примем следующий характер расположения полей допусков соответствующих размеров.

А1=48 h10(-0,1)

A2=30 h10(-0,1)

A3=80 h10(-0,12)

Сведем данные для расчета в таблицу

Таблица расчетных данных

Обозначение размера
Размера
ξj
Ecj
ξj Ecj

A1
А1=48h10(-0,1)
-I
-Ес1
Ес1

A2
A2=30h10(-0,1)
-I
-0,05
+0,05

A3
A3=80h10(-0,12)
+I
-0,06
-0,06

По уравнению найдем среднее отклонение замыкающего размера и сравним его с заданным:



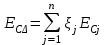
ЕСΔ=0,05+0,05-0,06=0,04

Так как полученное значение не совпадает с заданным, то произведем увязку средних отклонений за счет среднего отклонения замыкающего размера А1, принятого в качестве увязочново. Величину среднего отклонения размера А1 найдем из следующего уравнения:

-0,015= -ЕС1+0,05-0,06

Откуда ЕС1 =0,005 мм

Предельные отклонения размера А1:

ES1= 0,005+0,5*0,1=0,055

EI1=0,005-0,5*0,1= -0,045

Таким образо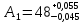м:

мм

Найти предельные значения замыкающего размера АΔ при значениях составляющих размеров, полученных в результате решения примера №1. Расчет произвести методом полной взаимозаменяемости.

Сведем данные для расчета в таблицу в таблицу

Обозначение размера
Размер
ξj
Nj
Ecj
Tj
ξj Nj
ξj Ecj
|ξj|Tj



А1
48h10(-0,1)
-I
40
-0,05
0,1
-48
+0,05
0,1

А2
30h10(-0,1)
-I
34
-0,05
0,1
-30
+0,05
0,1

А3
80h10(0,12)
+I
75
-0,06
0,12
+80
-0,06
0,12



  1. Номинальное значение замыкающего размера

NΔ= -48-30+80=2 мм

  1. Среднее отклонение замыкающего размера

ЕСΔ= 0,05+0,05-0,06= 0,04

  1. Допуск замыкающего размера

ТΔ= 0,1+0,1+0,12=0,32

Допуски на составляющие размеры можно оставить без изменений

  1. Предельные отклонения замыкающего размера

АΔмах=1-0,04+0,5*0,32=1,2

АΔmin=1-0,04-0,5*0,32=0,8

  1. Сравним полученные результаты с заданными

АΔmax расч=1,2= АΔmax задан=1,2

АΔmin расч=0,8 = АΔmin задан=0,82

Т.к. условие не выполняются то осуществляем расчет значений АΔmax и АΔmin





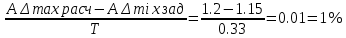
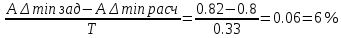
  1. Согласно заданию:

NΔ=1 мм – номинальное значение замыкающего размера

ТΔ=0,15-(-0,18)=0,33 мм – допуск замыкающего размера



Среднее отклонение замыкающего размера

АΔmax=1+0,15=1,2

AΔmin=1+(-0,18)=0,8

  1. Строим график размерной цепи



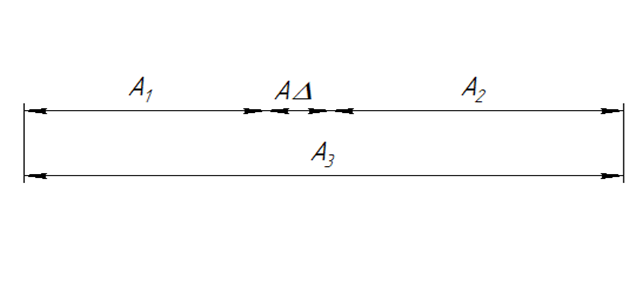
  1. Составим уравнение размерной цепи:

Общий вид уравнения размерной цепи описывается выражением:





Значение передаточных отношений

Обозначение передаточных отношений
ξ1
ξ2
ξ3

Числовое значение
-I
-I
+I

  1. Проведем проверку назначения номинальных значений составляющих размеров:



NΔ= -48-30+80=2

Так как по условию задачи NΔ=2 мм, следовательно, номинальные размеры назначены правильно.

  1. Осуществим привязку допусков, для чего исходя из величины ТΔ рассчитаем допуски соответствующих размеров



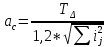
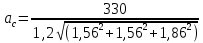=95

  1. По приложению Ⅰ устанавливаем, что полученное значение ас больше принятого для квалитета 11, но меньше, чем для квалитет 12

Установим для всех размеров допуски по 11 квалитету:

Т1 = 0,16 мм Т2 =0,16 мм Т3 =0,19 мм

  1. Произведем проверку правильности назначения допусков соответствующих размеров по уравнению:

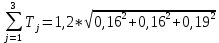=0,35

Полученная сумма допусков меньше заданного допуска замыкающего размера. Для того, чтобы полностью использовать заданный допуск замыкающего размера, расширим допуск замыкающего размера А1 и найдем его из уравнения:



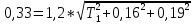
Откуда Т1=0,01

  1. Осуществим увязку средних отклонений. Увязку будем производить за счет среднего отклонения размера А1 , принятого в качестве увязочново.

Примем следующий характер расположения полей допусков соответствующих размером.

А1=48 h11(-0,16)

A2=30 h11(-0,16)

A3=80 h11(-0,19)

Сведем данные для расчета в таблицу

Обозначение разме-ра
Размер
ξj
Ecj
Ti
αi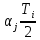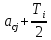




ξj( )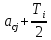

А1
48 h11(-0,16)
-I
EC1
0,16
0,2
0,016
EC1+0,16
-(EC1+0,016)

А2
30 h11(-0,16)
-I
-0,08
0,16
0,2
0,016
-0,064
0,064

А3
80 h11(-0,19)
+I
-0,095
0,19
0,2
0,019
-0,076
-0,076

Из уравнения найдем среднее отклонение размера А1

-0,015= -(ЕС1+0,16)+0,064-0,076

Откуда ЕС1=0,01

Предельные отклонения размера А1:

ES1=0,01+0,5*0,064=0,038

EI1=0,021-0,5*0,21= -0,025

Таким образом

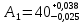
Найти предельные значения замыкающего размера А1 при значении соответствующий размеров, полученных в результате решения примера №3. Расчет произвести вероятностным методом, исходя из допустимого брака на сборке равного, 0,27%.

Сведем данные для расчетов в таблицу

  1. Номинальное значение замыкающего размера

NΔ= -48-30+80=2

  1. Среднее отклонение замыкающего размера

ЕСΔ=( -0,189+0,064)+0,064-0,076 = 0,015

  1. Допуск замыкающего размера



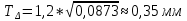
  1. Предельные значения замыкающего размера

АΔmax =1-0,015+0,5*0,35=1,2 мм

AΔmin =1-0,015-0,5*0,36=0,8 мм

  1. Сравним полученные результаты с заданными

АΔmax =1,2 = АΔmax расч=1,2

AΔmin =0,8 = AΔmin расч=0,8

Следовательно изменение предельных отклонений соответствующих размеров не требуется.


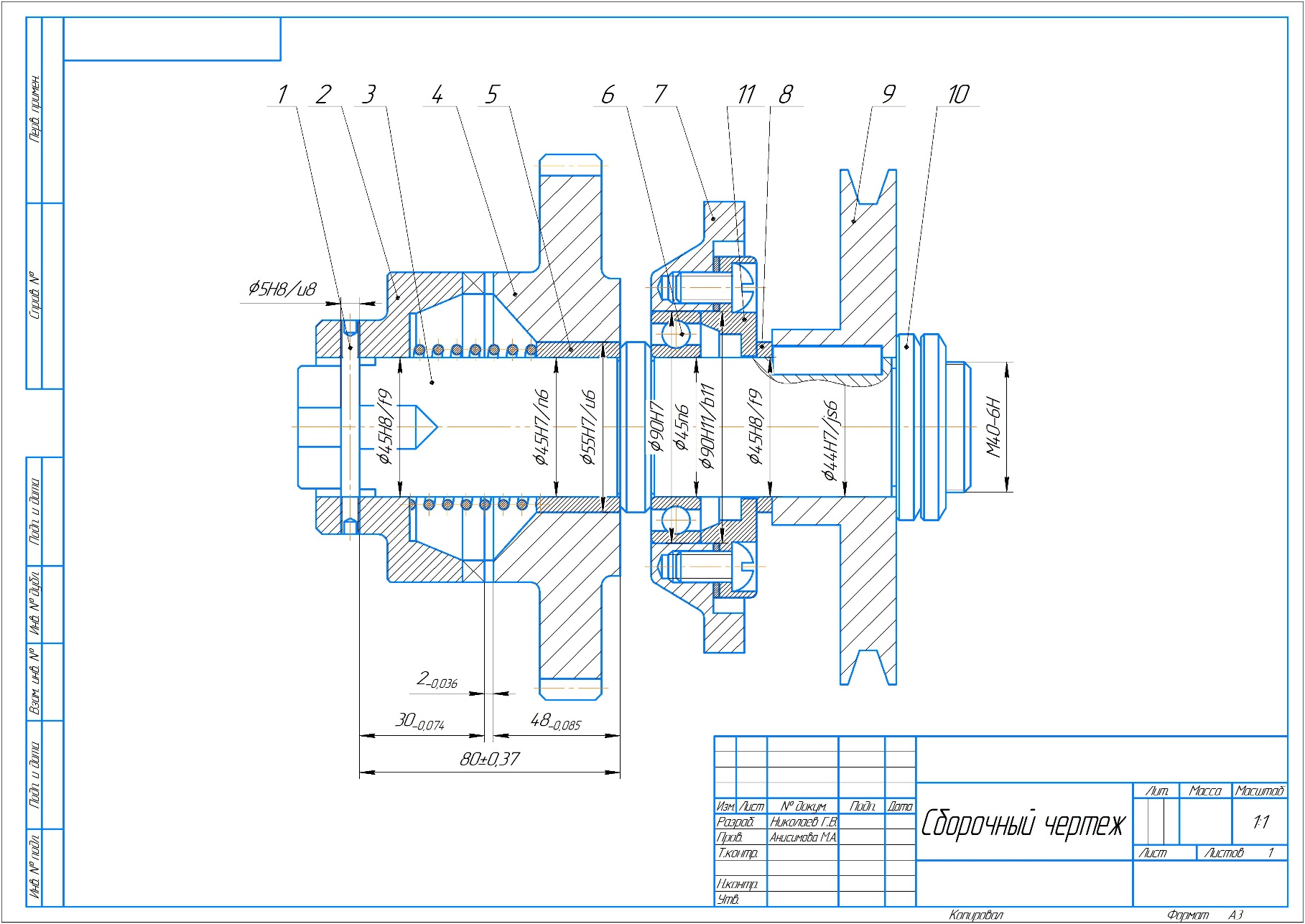
Приложение 1 –Сборочный чертеж

Приложение 2 – Чертеж шкива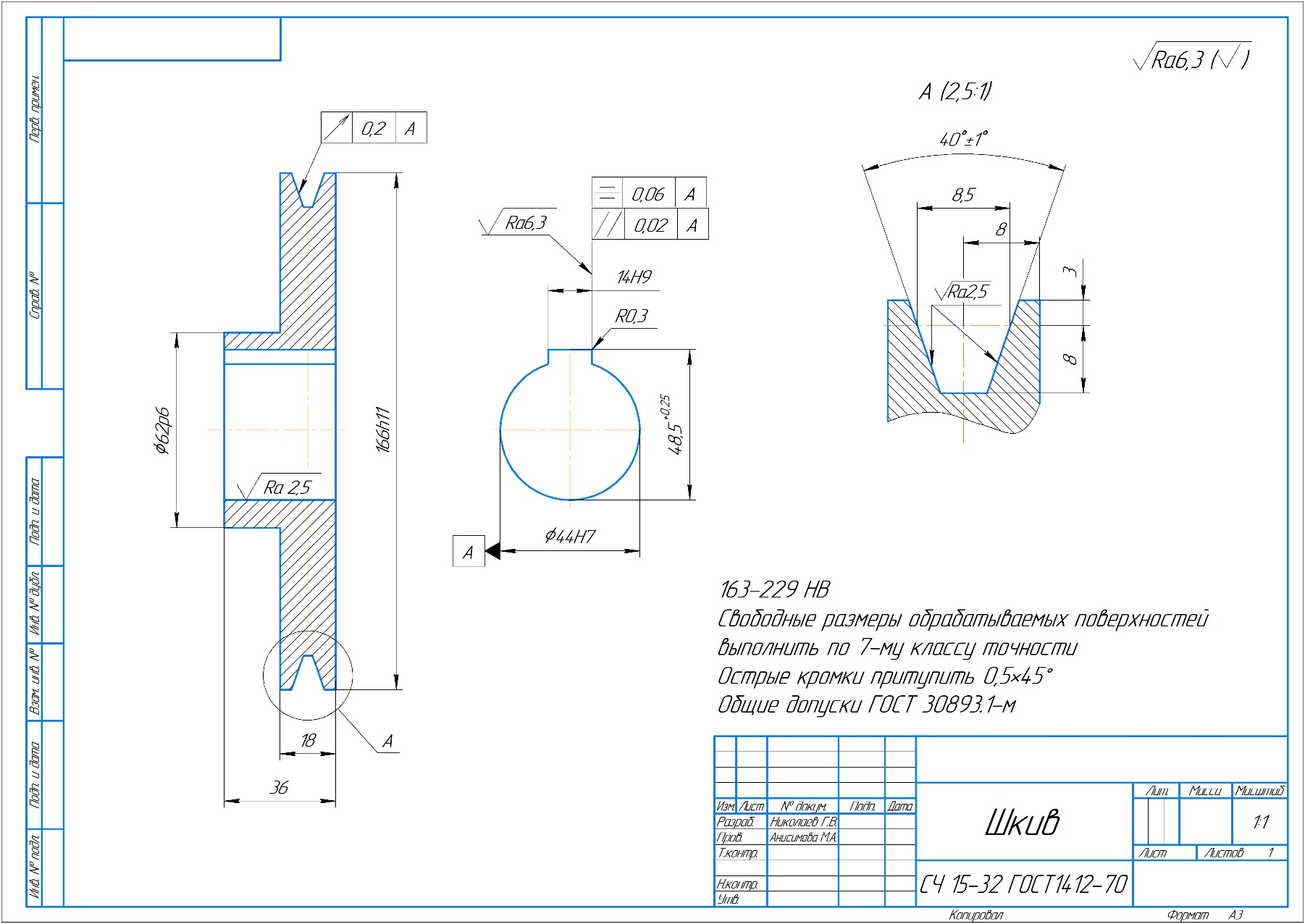

Приложение 3 – Чертеж вала

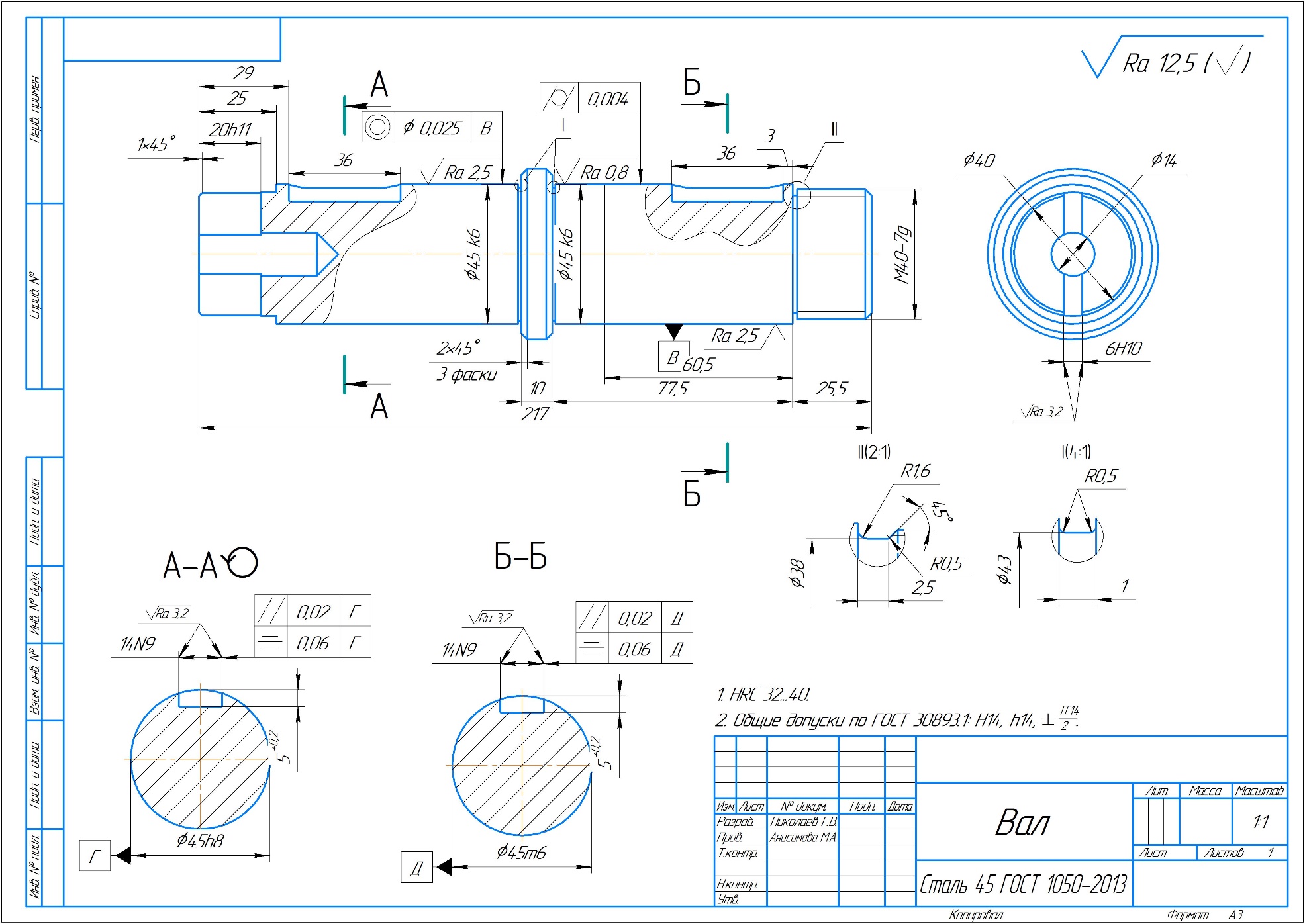Заключение

В данной курсовой работе были подобраны допуски для различных видов посадок, построены для них поля допусков и по схемам определены предельные размеры и отклонения, максимальные и минимальные зазоры и натяги.

Были разработаны конструкторские чертежи двух деталей, для одного из расчетных соединений с указанием точности размеров, отклонений форм, расположения и шероховатость посадочных поверхностей.

Нарисовали схему расположения полей допусков подшипника на вал и в корпус.

Выполнили расчет размерной цепи методом полной взаимозаменяемости и теоретико-вероятностным методом.

Оформили сборочный чертеж заданного узла с указанием назначенных посадок. Указали размеры на чертежах узла и деталей, не указанные в задании, выполненные по общим масштабным соотношениям чертежа задания.


Список использованной литературы

  1. Якушев А.И., Воронцов Л.Н., Федотов Н.М. Взаимозаменяемость, стандартизация и технические измерения: Учебник для втузов. М.: Машиностроение, 1987. – 352с.

  2. Мягков В.Д., Палей М.А., Романов А.Б., Брагинский В.А. Допуски и посадки: Справочник. В 2-х ч. Т.1 - 6-е изд., перераб. и доп. Л.: Машиностроение. Ленингр. отд-ние, 1982. - 4.1, - 543 с.

  3. Мягков В.Д., Палей М.А., Романов А.Б., Брагинский В.А. Допуски и посадки: Справочник. В 2-х ч. Т.2 - 6-е изд., перераб. и доп. - Л.: Машиностроение. Ленингр. отд-ние, 1982. - 4.2. - 448 с.

  4. Дунаев П.Ф., Лешков О.П. Конструирование узлов и деталей машин. – 4-е изд., перераб. и доп. М.: Высшая школа, 1985. – 416 с.

  5. Методические указания по выполнению курсовой работы.

  6. ГОСТ 25347-82 Основные нормы взаимозаменяемости. Единая система допусков и посадок. Поля допусков и рекомендуемые посадки. Введ. 1983-07-01. М.: ИПК Издательство стандартов, 2004.

  7. ГОСТ 2.109-73 Единая система конструкторской документации. Основные требования к чертежам. Взамен ГОСТ 2.107-68, ГОСТ 2.109-68, ГОСТ 5292-60 в части разд.VIII; введ. 1974-07-01. М.: Стандартинформ, 2011.

  8. ГОСТ 2.302-68 Единая система конструкторской документации. Масштабы. Взамен ГОСТ 3451-59; введ. 1971-01-01. Сб. ГОСТов. - М.: Стандартинформ, 2007.

  9. ГОСТ 2.305-2008 Единая система конструкторской документации (ЕСКД). Изображения - виды, разрезы, сечения. Взамен ГОСТ 2.305-68; введ. 2009-07-01. АО "Кодекс".

  10. ГОСТ 2.307-2011 Единая система конструкторской документации (ЕСКД). Нанесение размеров и предельных отклонений. Взамен ГОСТ 2.307-68; введ. 2012-01-01. АО "Кодекс"

  11. ГОСТ 2.308-2011 Единая система конструкторской документации. Указание допусков формы и расположения поверхностей. Взамен ГОСТ 2.308-79; введ. 2012-01-01. М.: Стандартинформ, 2012.

  12. ГОСТ 30893.1-2002 (ИСО 2768-1-89) Основные нормы взаимозаменяемости. Общие допуски. Предельные отклонения линейных и угловых размеров с неуказанными допусками. Взамен ГОСТ 25670-83; введ.  2004-01-01. М.: ИПК Издательство стандартов, 2003.

  13. ГОСТ 2.309-73 Единая система конструкторской документации. Обозначения шероховатости поверхностей. Взамен ГОСТ 2.309-68; введ. 1975-01-01. Сб. ГОСТов. - М.: Стандартинформ, 2007.

  14. ГОСТ 6636-69 Основные нормы взаимозаменяемости. Нормальные линейные размеры. Взамен ГОСТ 6636-60; введ. 1970-01-01. М.: ИПК Издательство стандартов, 2004.

  15. ГОСТ 25346-89 Основные нормы взаимозаменяемости. Единая система допусков и посадок. Общие положения, ряды допусков и основных отклонений. Взамен ГОСТ 25346-82; введ. 1990-01-01. М.: ИПК Издательство стандартов, 2004.

Смотрите также файлы