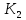Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский авиационный институт (национальный исследовательский университет)»

Институт № 3 «Системы управления, информатика и электроэнергетика»Кафедра №301 «Системы автоматического и интеллектуального управления»Направление подготовки 24.05.06 «Системы управления летательными аппаратами»О Т Ч Е Т

По лабораторной работе

Название:Моделирование непрерывных и цифровых систем автоматического управленияДисциплина: Моделирование систем

Студенты	М3О-401С-19		М.М. Заруднева
	(Группа)	(Подпись, дата)	(И.О. Фамилия)
			А.Д. Нелюбова
		(Подпись, дата)	(И.О. Фамилия)
Преподаватель			П.В. Мулин
		(Подпись, дата)	(И.О. Фамилия)

---

Москва, 2023Цель: Проверка владения методами синтеза и анализа непрерывных, цифровых систем автоматического управления (САУ) с использованием средств САПР.Задание 1: Осуществить параметрический синтез контуров непрерывной САУ, заданной структурной схемой (рис. 1), удовлетворяющих следующим требованиям к показателям качества переходной функции:

1. 
   Внутренний контур:
   

– Перерегулирование σ <5%;– Время переходного процесса минимально;

2. 
   Внешний контур:
   

– Перерегулирование σ <0%;– Время переходного процесса минимально.Рисунок 1 – Структурная схема непрерывной иерархической САУИсходные данные (вариант №3): 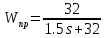, , 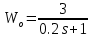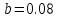.Ход работы:

1. 
   Создадим модель разомкнутого внутреннего контура САУ (рис. 2) и определим по ней передаточную функцию разомкнутой системы:
   

Рисунок 2 – Модель разомкнутого внутреннего контура САУW = tf(linsys1)W =From input "Step1" to output "Integrator1":144-------------------s^3 + 23 s^2 + 90 sName: Linearization at model initial conditionContinuous-time transfer function.

2. 
   Построим корневой годограф для внутреннего контура системы (рис. 3):
   

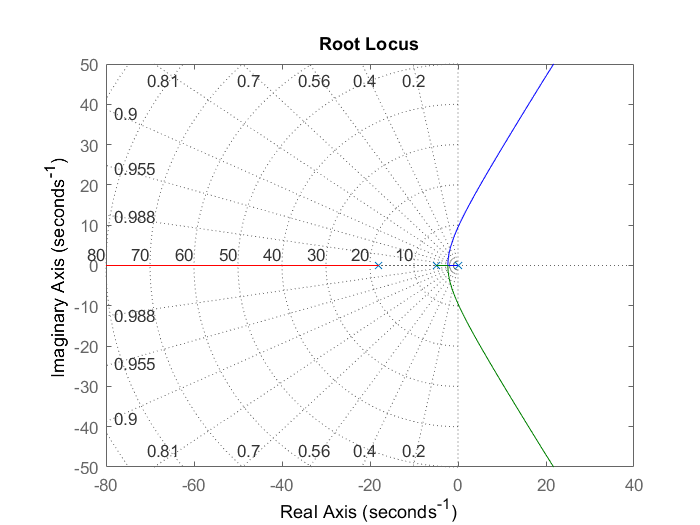
rlocus(linsys1), sgrid Рисунок 3 – Корневой годограф внутреннего контура системы

3. 
   Выберем значение коэффициента усиления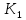 , обеспечивающее заданные показатели качества к переходной функции:
   

[k, poles]=rlocfind(linsys1)selected_point = -2.1656 + 2.1823ik = 1.2208poles = 3×1 complex-18.6873 + 0.0000i-2.1564 + 2.1811i-2.1564 - 2.1811iПостроим переходный процесс (рис. 4) и определим прямые показатели качества системы (таблица 1):

---

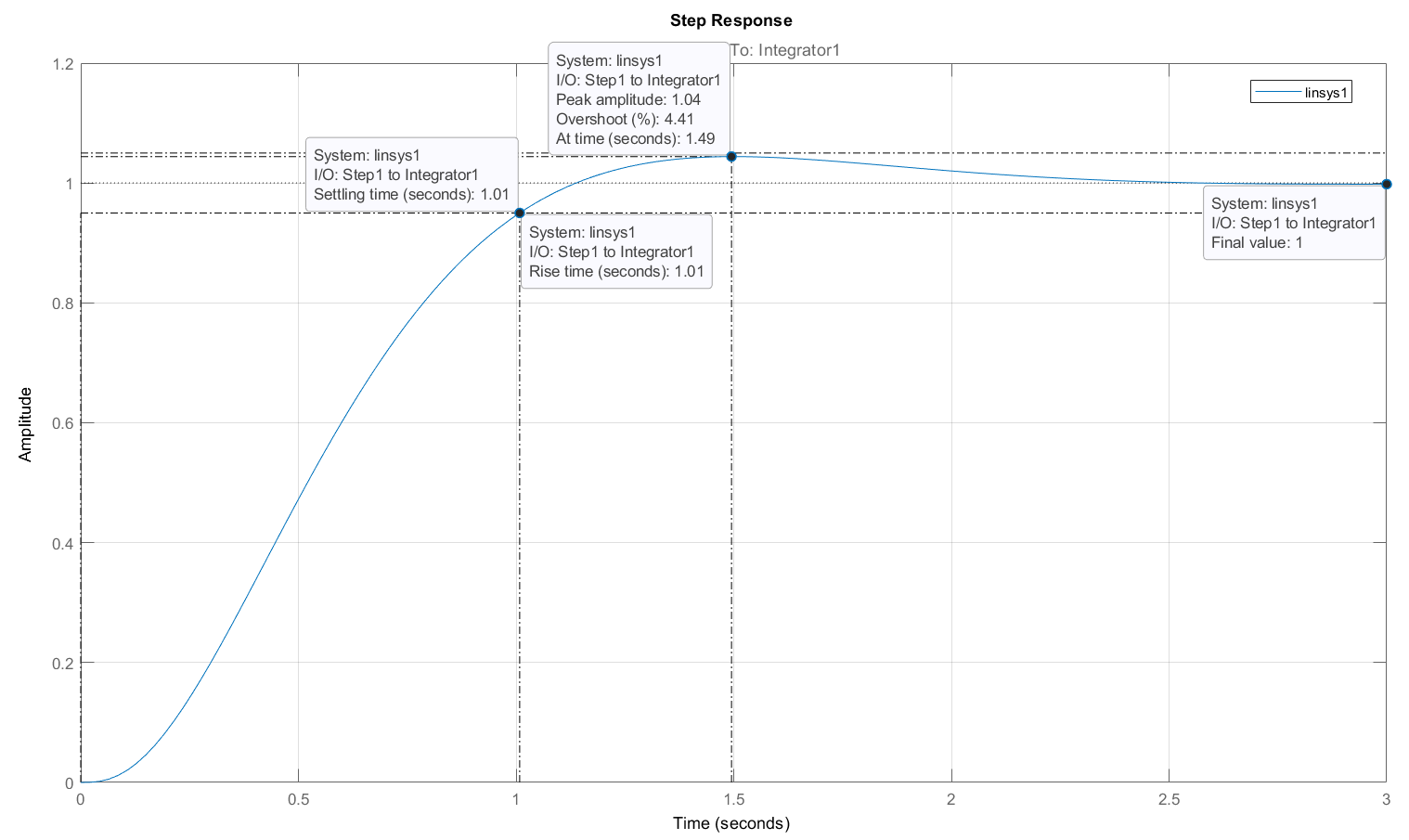
Рисунок 4 – Переходный процесс внутреннего контура системыТаблица 1 – Прямые показатели качества переходного процесса

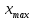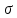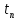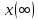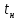1.49	4.41%	1.01	1	1.01

4. 
   Построим амплитудно-частотную характеристику внутреннего контура системы (рис. 5):
   

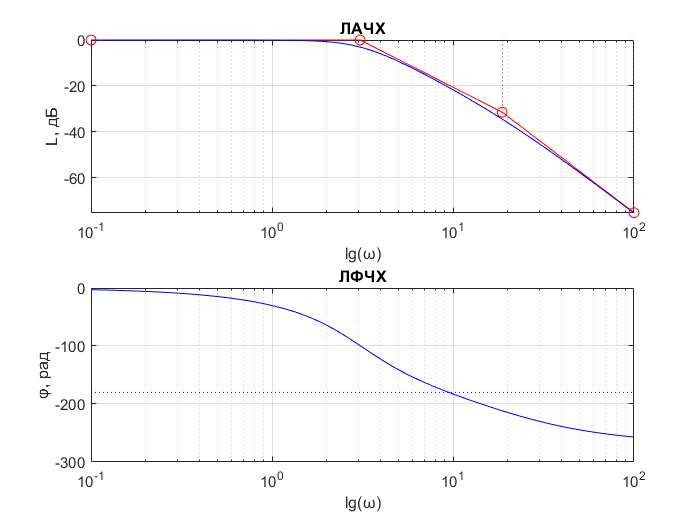
Рисунок 5 – ЛАЧХ внутреннего контура системыОпределим значение частоты, начиная с которой выполняется условие для амплитудно-частотной характеристики :

5. 
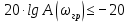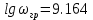
   Определим передаточную функцию замкнутого внутреннего контура системы:
   

W = tf(linsys1)W =From input "Step1" to output "Integrator1":175.8---------------------------s^3 + 23 s^2 + 90 s + 175.8Name: Linearization at model initial conditionContinuous-time transfer function.

6. 
   Создадим модель разомкнутого внешнего контура САУ (рис. 6) и определим по ней передаточную функцию разомкнутой системы:
   

Рисунок 6 – Модель разомкнутого внешнего контура САУW = tf(linsys1)W =From input "Step" to output "Transfer Fcn2":21.1-------------------------------s^4 + 23 s^3 + 90 s^2 + 175.8 sName: Linearization at model initial conditionContinuous-time transfer function.

7. 
   Построим корневой годограф для внешнего контура системы (рис. 7):
   

rlocus(linsys1), sgrid

---

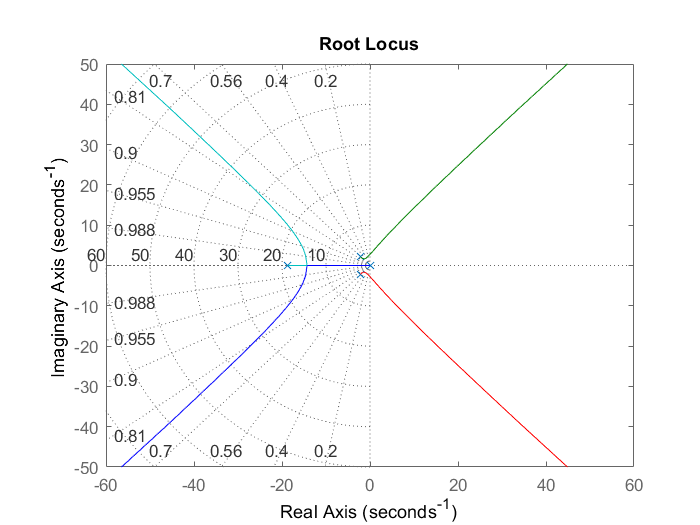
Рисунок 7 – Корневой годограф внутреннего контура системы

8. 
   Выберем значение коэффициента усиления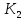 , обеспечивающее заданные показатели качества к переходной функции:
   

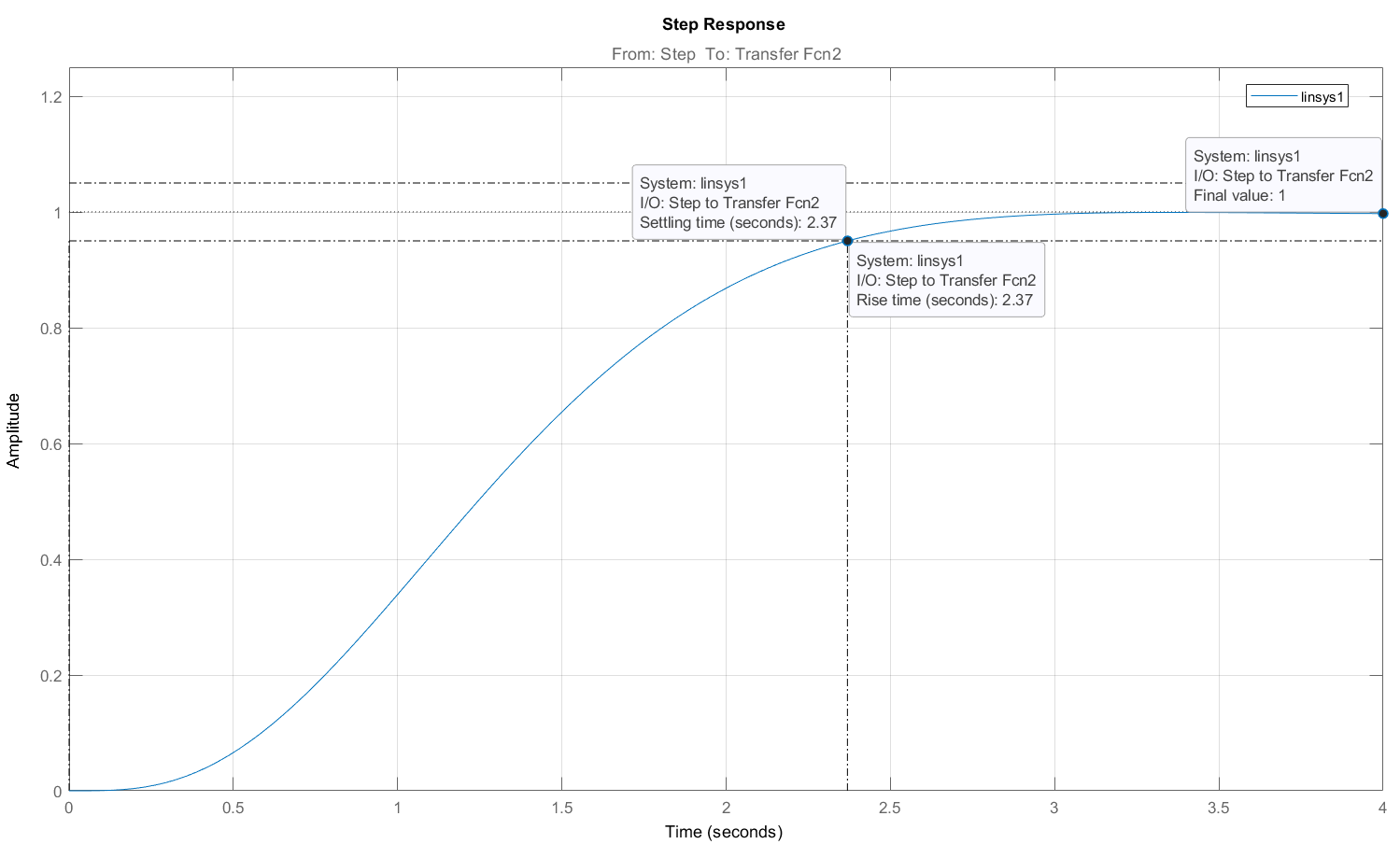
[k, poles]=rlocfind(linsys1)selected_point = -1.4437 + 1.4121ik = 6.3613poles = 4×1 complex-18.6614 + 0.0000i-1.4147 + 1.6623i-1.4147 - 1.6623i-1.5092 + 0.0000iПостроим переходный процесс (рис. 8) и определим прямые показатели качества системы (таблица 2):Рисунок 8 – Переходный процесс внешнего контура системыТаблица 2 – Прямые показатели качества переходного процесса

1	0%	2.37	1	2.37

9. 
   Построим амплитудно-частотную характеристику внешнего контура системы (рис. 9):
   

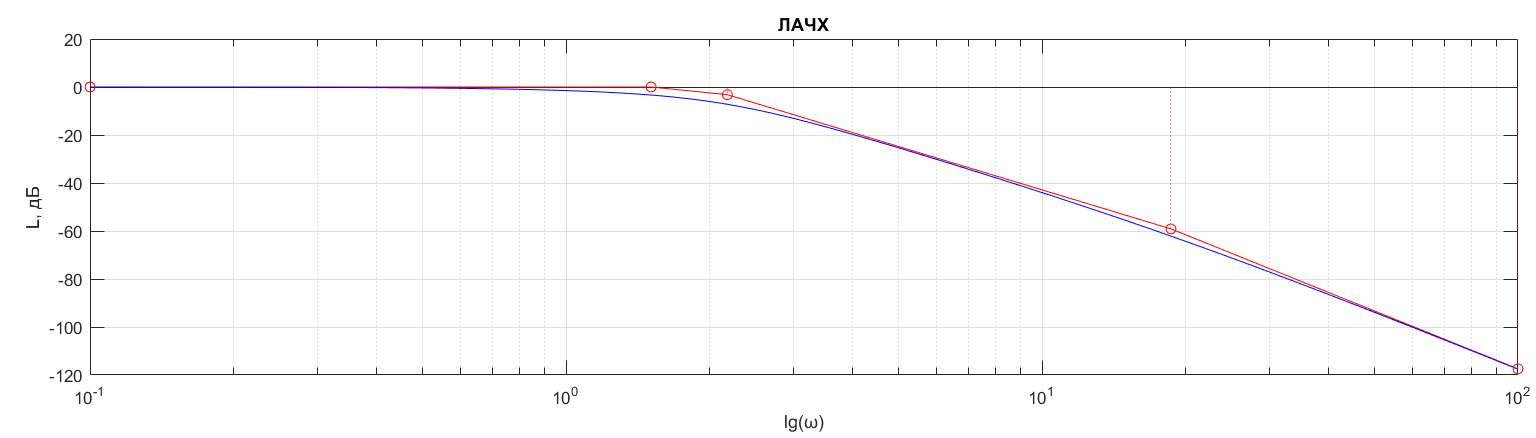
Рисунок 9 – ЛАЧХ внешнего контура системыОпределим значение частоты, начиная с которой выполняется условие для амплитудно-частотной характеристики :

10. 
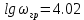
    Определим передаточную функцию замкнутого внутреннего контура системы:
    

W = tf(linsys1)W =From input "Step" to output "Transfer Fcn2":134.2---------------------------------------s^4 + 23 s^3 + 90 s^2 + 175.8 s + 134.2Name: Linearization at model initial conditionContinuous-time transfer function.Задание 2: Осуществить параметрический синтез и анализ цифровой САУ по непрерывному аналогу (рис. 1), структурная схема цифровой САУ представлена на (рис. 10).

---

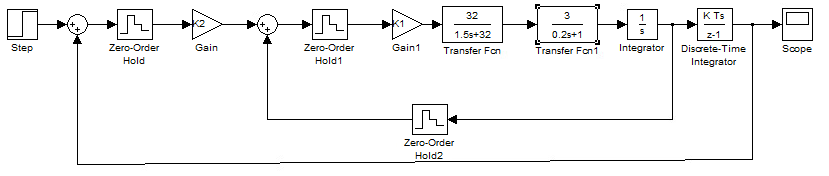
Рисунок 10 – Структурная схема иерархической цифровой САУ

1. 
   Найдём период дискретности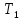 для внутреннего контура:
   

T = pi/(3*9.164)T = 0.1143

2. 
   Создадим модель цифрового внутреннего контура (рис. 11):
   

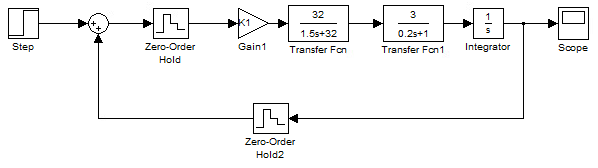
Рисунок 11 – Модель цифрового внутреннего контура САУ

3. 
   Выберем значение коэффициента усиления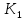 для цифрового внутреннего контура (рис. 11), при котором обеспечивается минимальное время переходного процесса, а перерегулирования не превышает значения перерегулирования для непрерывного аналога внутреннего контура:
   

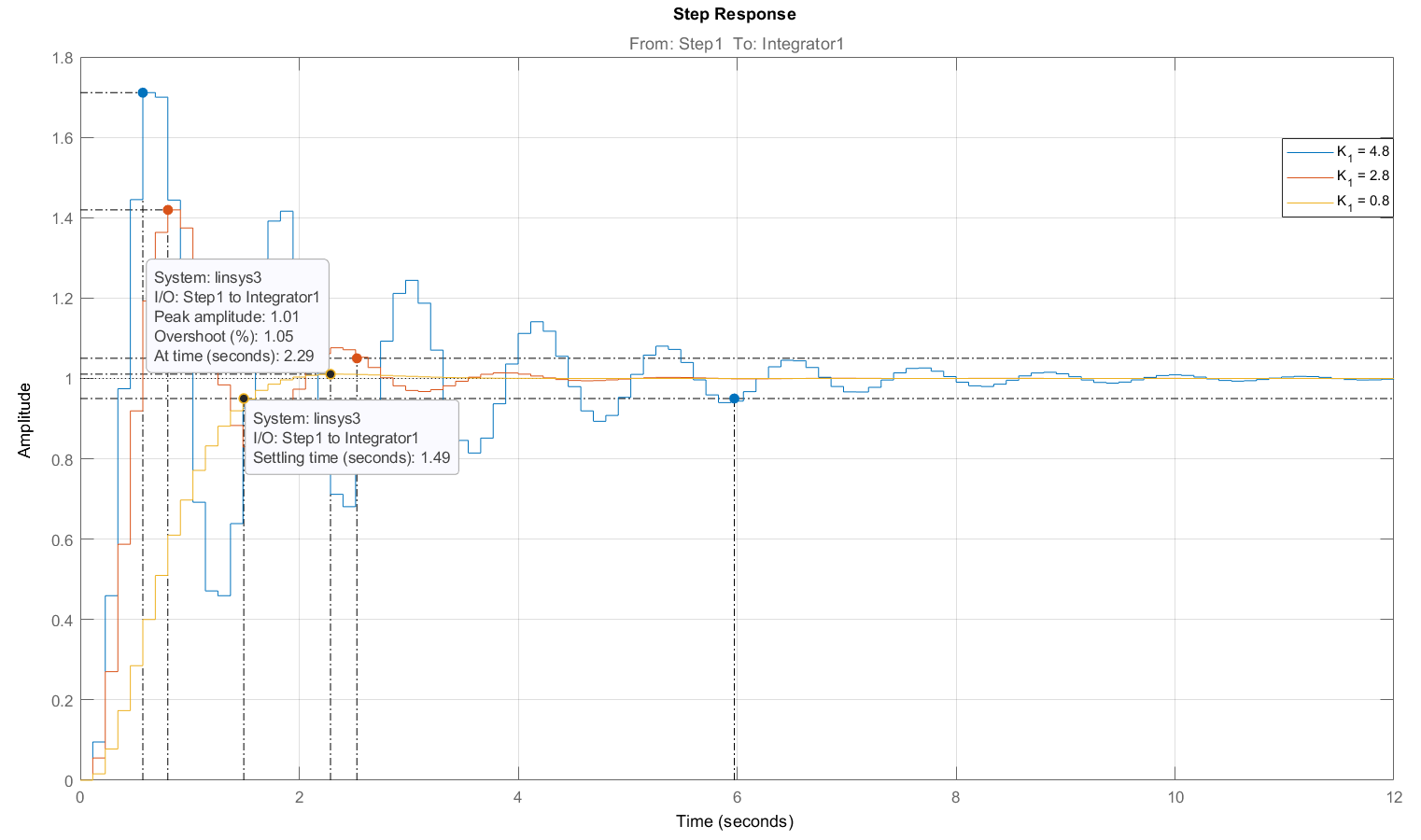
Рисунок 12 – Варьирование коэффициента 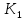в переходном процессе внутреннего контураНа основании представленных переходных процессов (рис. 12) коэффициент 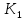возьмем равным 0.8.

4. 
   Найдём период дискретности :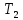
   

T = pi/(3*4.02)T = 0.2605

5. 
   Создадим модель цифрового внешнего контура (рис. 13):
   

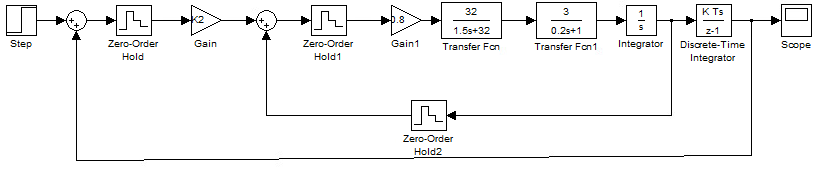
Рисунок 13 – Модель цифрового внешнего контура САУ

6. 
   Выберем значение коэффициента усиления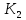 для цифрового внешнего контура (рис. 13), при котором обеспечивается минимальное время переходного процесса, а перерегулирования не превышает значения перерегулирования для непрерывного аналога внешнего контура:
   

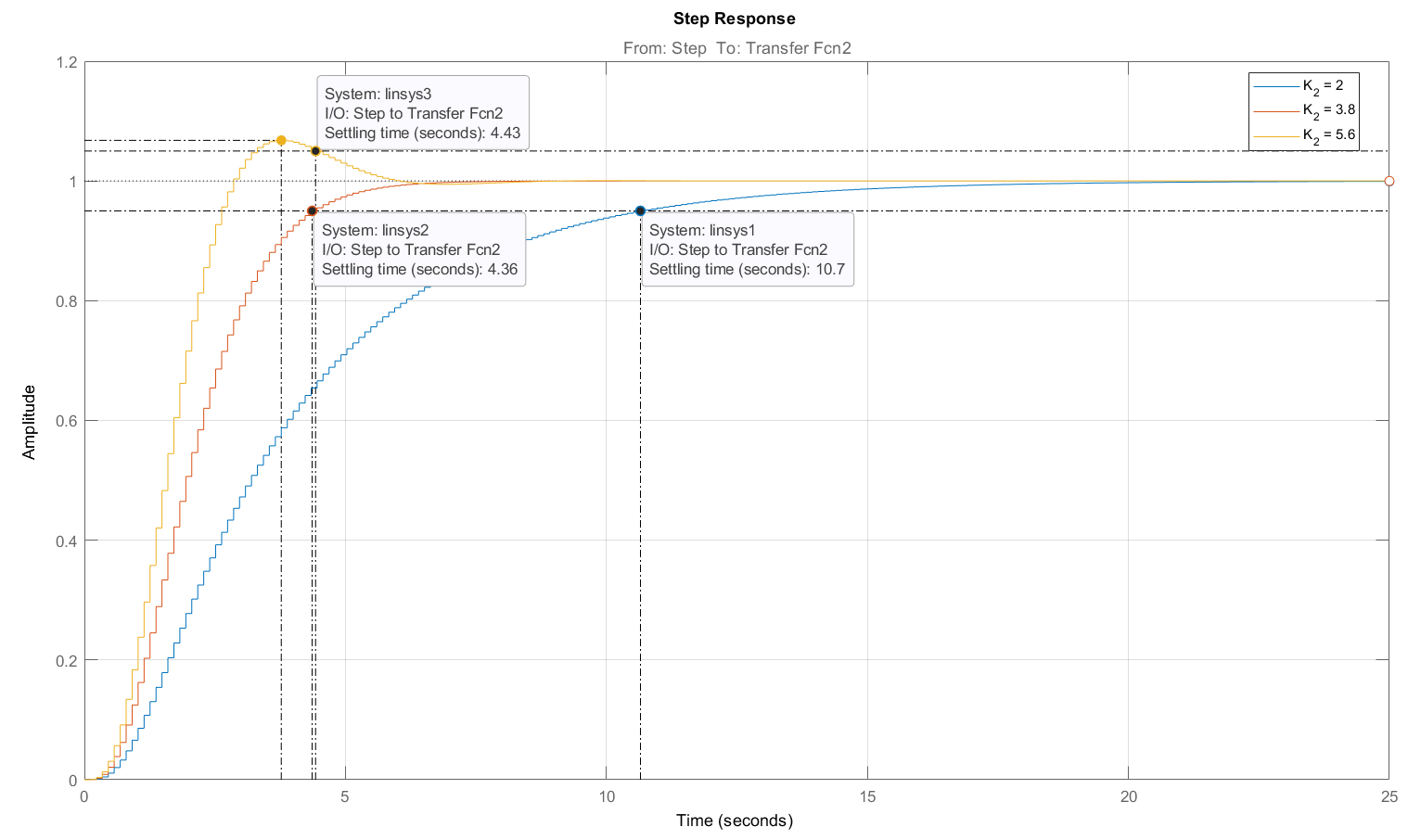
Рисунок 14 – Варьирование коэффициента 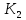в переходном процессе внутреннего контураНа основании представленных переходных процессов (рис. 14) коэффициент

---

Смотрите также файлы

• Реферат по дисциплине Физическая культура и спорт на тему взаимосвязь физической и умственной деятельности человека.doc

• 1. Понятие о системе разработки залежей нефти. Рациональная система разработки. Параметры системы разработки. Система разработки.docx

• Ед. Измерения.doc

• Международная практика и эффективность введения валютных ограничений.doc

• Национальная безопасность России. Основы мобилизационной подготовки и мобилизации здравоохранения.rtf