Добавлен: 30.11.2023
Просмотров: 72
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Рисунок 5 – График распределения исходных данных и линейной модели
Проведём анализ полученной модели для определения её достоверности (рис. 6).
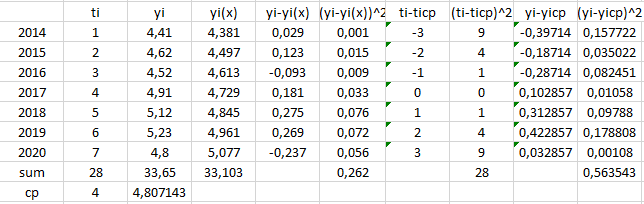
Рисунок 6 – Анализ полученной линейной модели
Для оценки качества выбранной модели рассчитывается коэффициент детерминации по следующей формуле:
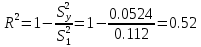
где:
‑ стандартная ошибка:
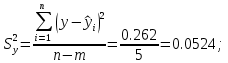
‑ расчёт полной дисперсии:
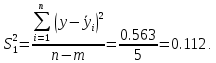
Так как коэффициент детерминации равен 52%, то можно сделать вывод о том, что данная модель является приемлемой.
Для окончания решения прогностической задачи был определён доверительный интервал:
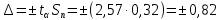
где
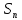 – среднее квадратическое отклонение прогноза, которое вычисляется по формуле:
– среднее квадратическое отклонение прогноза, которое вычисляется по формуле: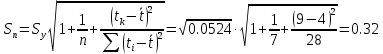
где
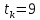 – период упреждения.
– период упреждения.Таким образом, прогноз на период с 2022 по 2023 годы имеет вид:
| 2022 | 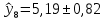 |
| 2023 | 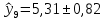 |
2.2. Полиномиальная модель 2-го порядка
Полиномиальная модель 2-го порядка имеет вид:
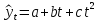
Для построения полиномиальной модели 2-го порядка была применена программа MS Excel:
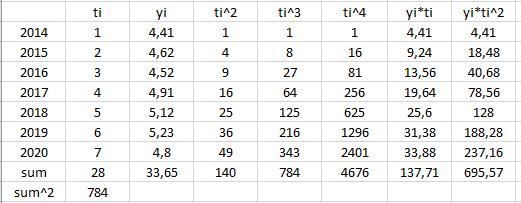
Рисунок 7 – Результаты расчёта полиномиальной модели 2-го порядка в программе MS Excel
Для расчёта параметров уравнения составим систему уравнений следующего вида:
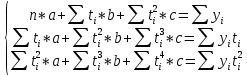
Получим следующую систему уравнений:
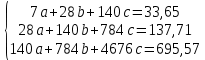
В результате использования метода Крамера для решения составленной системы уравнений были получены следующие корни системы уравнений:
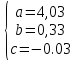
В результате была получена полиномиальная модель 2-го порядка для исследуемой статистики:
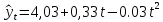
Согласно полученной модели, построим прогноз на период 2022-2023г. (согласно правилу, что количество прогнозных точек приблизительно равно трети от исследуемого периода) (рис. 8).
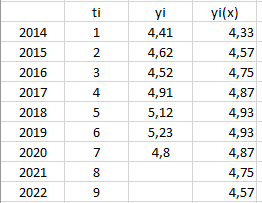
Рисунок 8 – Прогноз по полиномиальной модели 2-го порядка
Сопоставим полученную математическую модель с фактическими данными на графике (рис. 9).
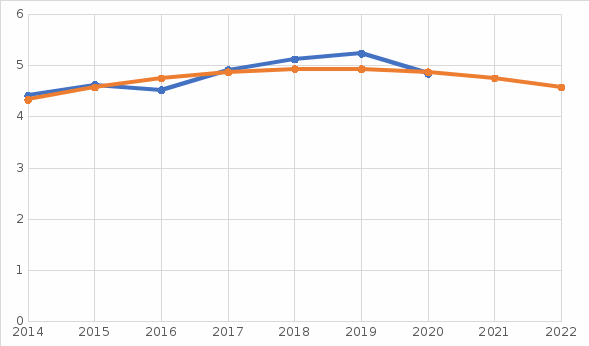
Рисунок 9 – График распределения исходных данных и полиномиальной модели 2-го порядка
Проведём анализ полученной модели для определения её достоверности (рис. 10).
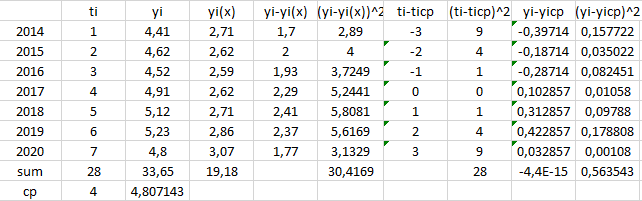
Рисунок 9 – Анализ полученной полиномиальной модели 2-го порядка
Для оценки качества выбранной модели рассчитывается коэффициент детерминации по следующей формуле:
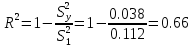
где:
‑ стандартная ошибка:
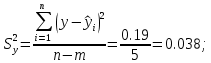
‑ расчёт полной дисперсии:
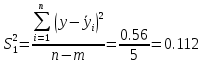
Так как коэффициент детерминации равен 66%, то можно сделать вывод о том, что данная модель является приемлемой.
Для окончания решения прогностической задачи был определён доверительный интервал:
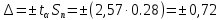
где
 – среднее квадратическое отклонение прогноза, которое вычисляется по формуле:
– среднее квадратическое отклонение прогноза, которое вычисляется по формуле: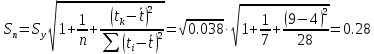
где
 – период упреждения.
– период упреждения.Таким образом, прогноз на период с 2022 по 2023 годы имеет вид:
| 2022 | 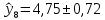 |
| 2023 | 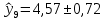 |
2.3. Полиномиальная модель 3-го порядка
Полиномиальная модель 3-го порядка имеет вид:
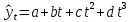
Для построения полиномиальной модели 3-го порядка была применена программа MS Excel:
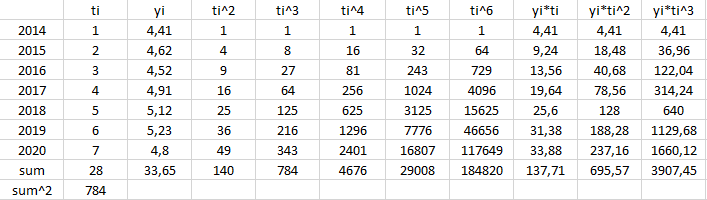
Рисунок 10 – Результаты расчёта полиномиальной модели 3-го порядка в программе MS Excel
Для расчёта параметров уравнения составим систему уравнений следующего вида:
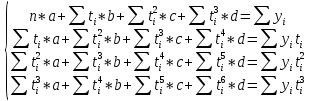
Получим следующую систему уравнений:
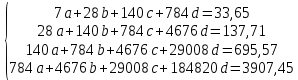
В результате использования метода Гаусса для решения составленной системы уравнений были получены следующие корни системы уравнений:
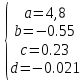
В результате была получена полиномиальная модель 3-го порядка для исследуемой статистики:
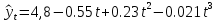
Согласно полученной модели, построим прогноз на период 2022-2023г. (согласно правилу, что количество прогнозных точек приблизительно равно трети от исследуемого периода) (рис. 11).
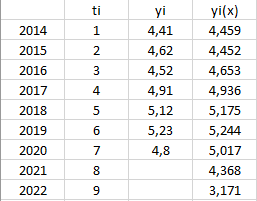
Рисунок 11 – Прогноз по полиномиальной модели 3-го порядка
Сопоставим полученную математическую модель с фактическими данными на графике (рис. 12).
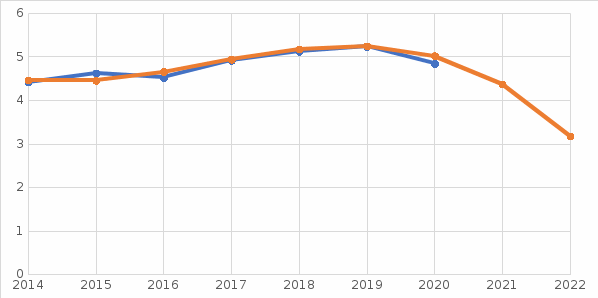
Рисунок 12 – График распределения исходных данных и полиномиальной модели 3-го порядка
Проведём анализ полученной модели для определения её достоверности (рис. 13).
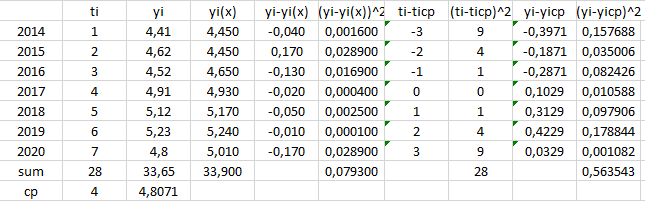
Рисунок 13 – Анализ полученной полиномиальной модели 3-го порядка
Для оценки качества выбранной модели рассчитывается коэффициент детерминации по следующей формуле:
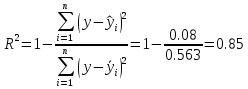
Стандартная ошибка:
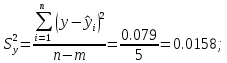
Расчёт полной дисперсии:
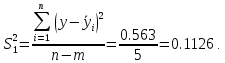
Так как коэффициент детерминации равен 85%, то можно сделать вывод о том, что данная модель является приемлемой.
Для окончания решения прогностической задачи был определён доверительный интервал:
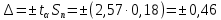
где
 – среднее квадратическое отклонение прогноза, которое вычисляется по формуле:
– среднее квадратическое отклонение прогноза, которое вычисляется по формуле: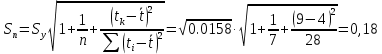
где
 – период упреждения.
– период упреждения.Таким образом, прогноз на период с 2021 по 2023 годы имеет вид:
| 2022 | 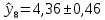 |
| 2023 | 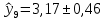 |
2.4. Выбор оптимальной прогнозной модели
В сводной таблице представлены коэффициенты детерминации для всех построенных моделей:
Таблица 1 – Сводная таблица коэффициентов детерминации
| Прогнозная модель | Коэффициент детерминации |
| Линейная модель | 0,52 |
| Полиномиальная модель 2-го порядка | 0,66 |
| Полиномиальная модель 3-го порядка | 0,85 |
Из сводной таблицы следует, что все модели являются приемлемыми.
Наиболее близким к единице коэффициентом детерминации обладает полиномиальная модель третьего порядка. Следовательно, прогноз следует строить именно на ее основе.
Заключение
В ходе работы было проанализировано состояние объема перевозок грузов воздушным транспортом. Объектом исследования был выбран весь сектор авиаперевозок, на основе данных Росавиации. На основании её статистики по объёмам перевозок грузов были построены различные прогнозные модели, целью которых является определение приблизительных показателей на ближнесрочную перспективу.
В результате выполнения работы была определена наиболее приемлемая модель, а также построены точечные и интервальные прогнозы.
По итогу выполнения работы была достигнута поставленная цель работы, а также выполнены основные задачи исследования.
Для выполнения работы использовалась программа Microsoft Excel.
Список используемой ЛИТЕРАТУРЫ
-
Орехов Н.А., Левин А.Г., Горбунов Е.А. Математические методы и модели в экономике. Учебное пособие для вузов / Под ред. проф. Н.А. Орехова – М.: ЮНИТИ-ДАНА, 2004. -
Моделирование сложных вероятностных систем: учеб. пособие / В. Г. Лисиенко, О. Г. Трофимова, С. П. Трофимов, Н. Г. Дружинина, П.А. Дюгай. Екатеринбург: УРФУ, 2011. 200 с. -
Хемди А.Т. Введение в исследование операций. – М.: Издательство ―Вильямс, 2005 – 912с.