Файл: Влияние качества напряжения сети на работу асинхронного двигателя.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 23
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
. Для исследования переходных процессов в АД необходимо будет изменять значения частоты питающего напряжения, что затрудняет использование блок-функций из стандартной библиотеки Simulink. Для решения этой проблемы необходимо реализовать пользовательский блок. Реализовать такой блок можно используя методику моделирования передаточных функций, изложенную в [1].
На рисунке 3 приведена разработка математической модели частотного регулирования. Согласно приведенной блок-схема (рис.3.) вычисление параметров схемы замещения приведена на рис. 4
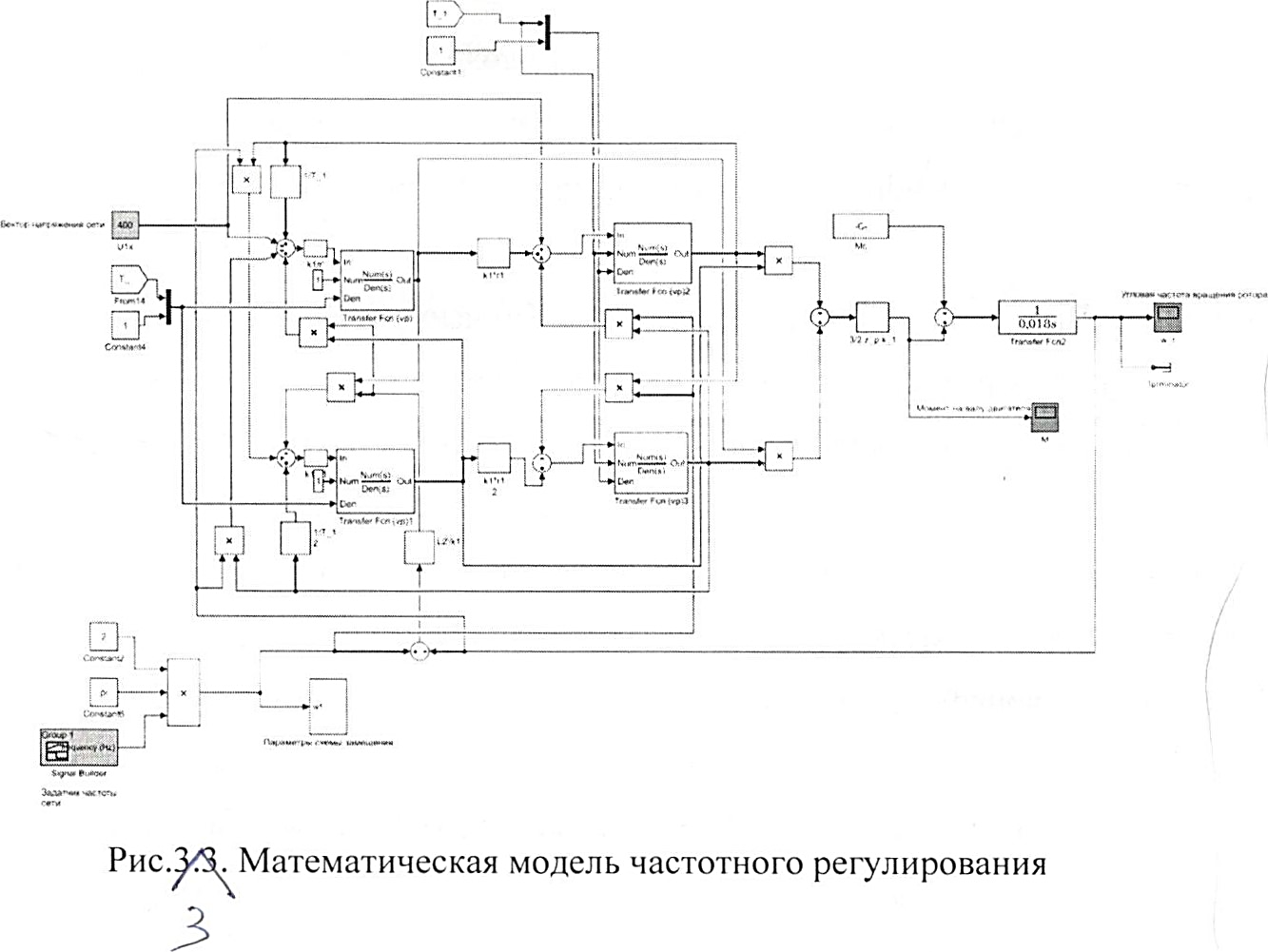
Рис.3. Математическая модель частотного регулирования
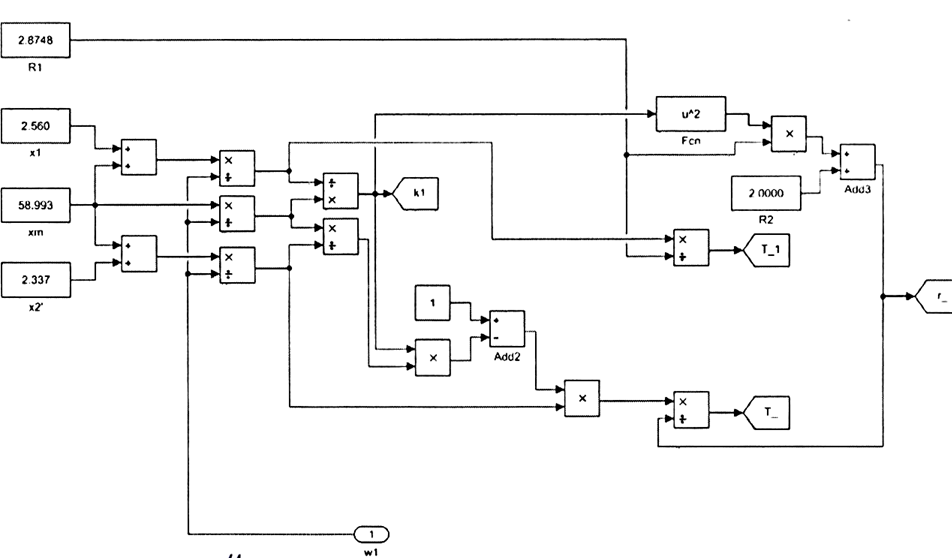
Рис. 4. Вычисление параметров схемы замещения.
Выходными характеристиками математической модели являются угловая скорость вращения ротора
и электромагнитный момент 
.
Частота сети задается функцией от времени f = F(t). Функция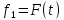 
приведена на рис 5.
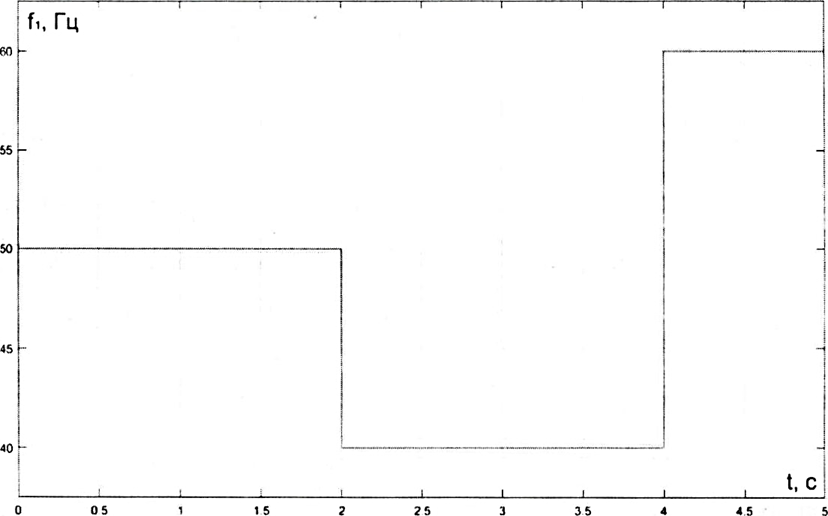
Рис. 5. График функции частоты тока сети от времени
На рисунке 6 приведен график угловой скорости вращения ротора = F(t). График изменения момента асинхронной машины от времени = F(t) приведен на рисунке 7.
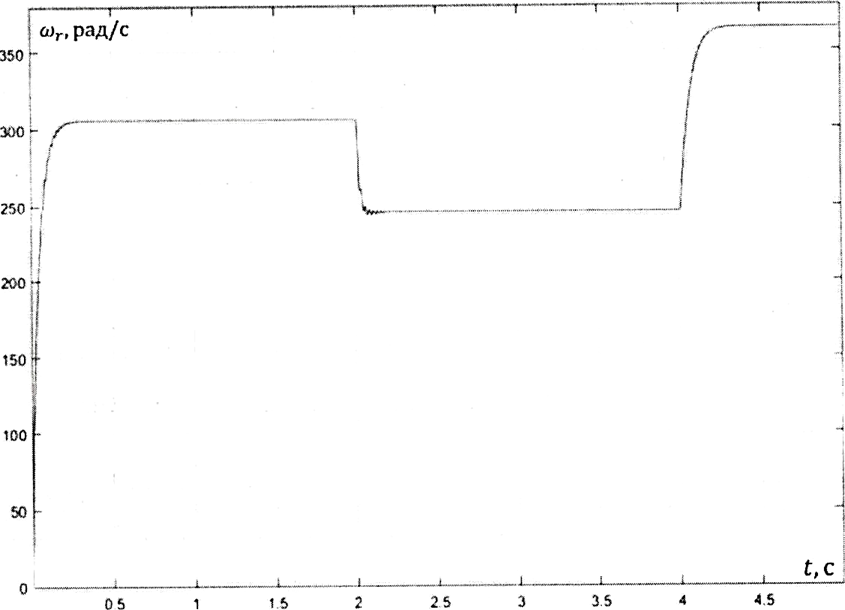
Рис.6. График угловой скорости вращения ротора.
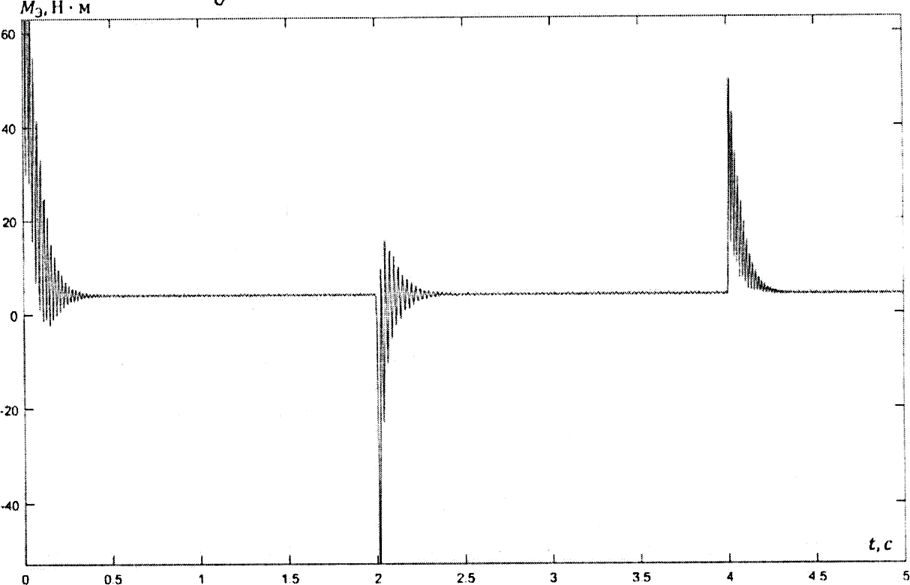
Рис.7. График изменения момента асинхронной машины
Для исследования асинхронного двигателя также удобна система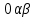
ортогональных координат, неподвижных относительно статора. Это удобство объясняется тем
, что в такой системе все электромагнитные величины, связанные с осью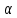
, равны соответствующим величинам фазы А естественной системы[6]. Система дифференциальных уравнений асинхронного двигателя в неподвижной системы координат 
[6]:
(18)
г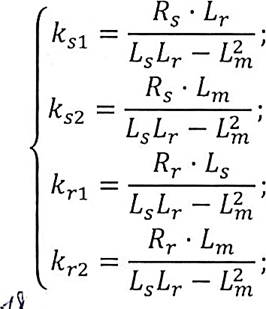
де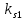
, 
, 
, 
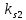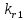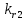определяются из уравнений:
Система уравнений (18) дает полную математическую модель АД. На основе вышеперечисленных уравнений методом Рунге-Кутта вычислим значения электромагнитного момента Мэ и угловую скорость вращения ротора .
Результаты расчетов получены программой блок- схема алгоритма работы программы для вычисления параметров асинхронного двигателя при разных значениях частоты питающей сети, приведена на рисунке 8. Подробный алгоритм работы программы приведен на рис 9.
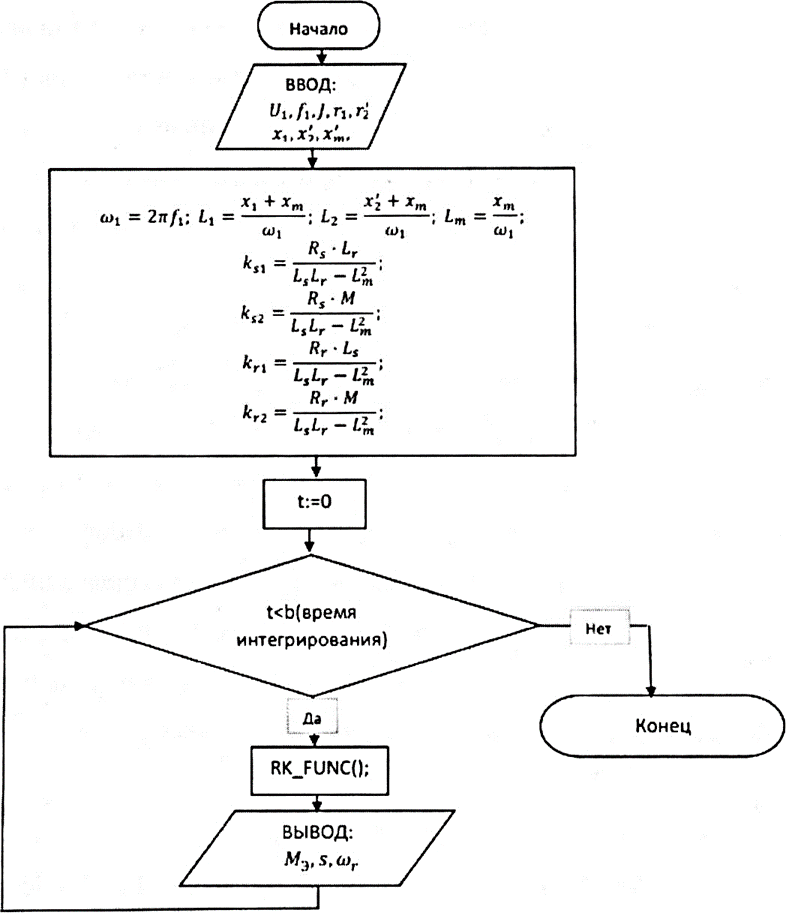
Рис. 8. Блок-схема алгоритма работы программы для вычисления параметров асинхронного двигателя при разных значения частоты питающей сети.
Рис.9. Функция численного интегрирования
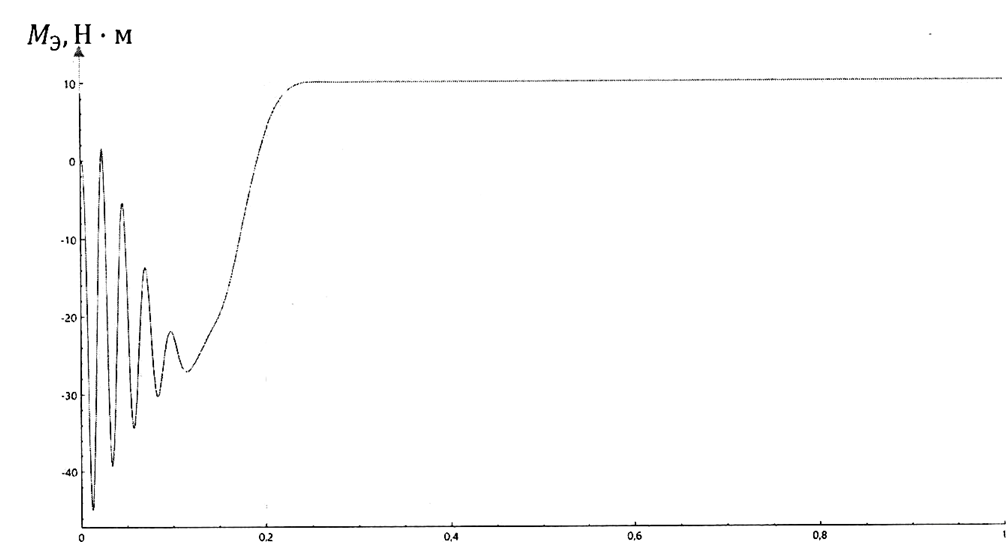
t,c
Рис.10. График изменения момента асинхронной машины
рад
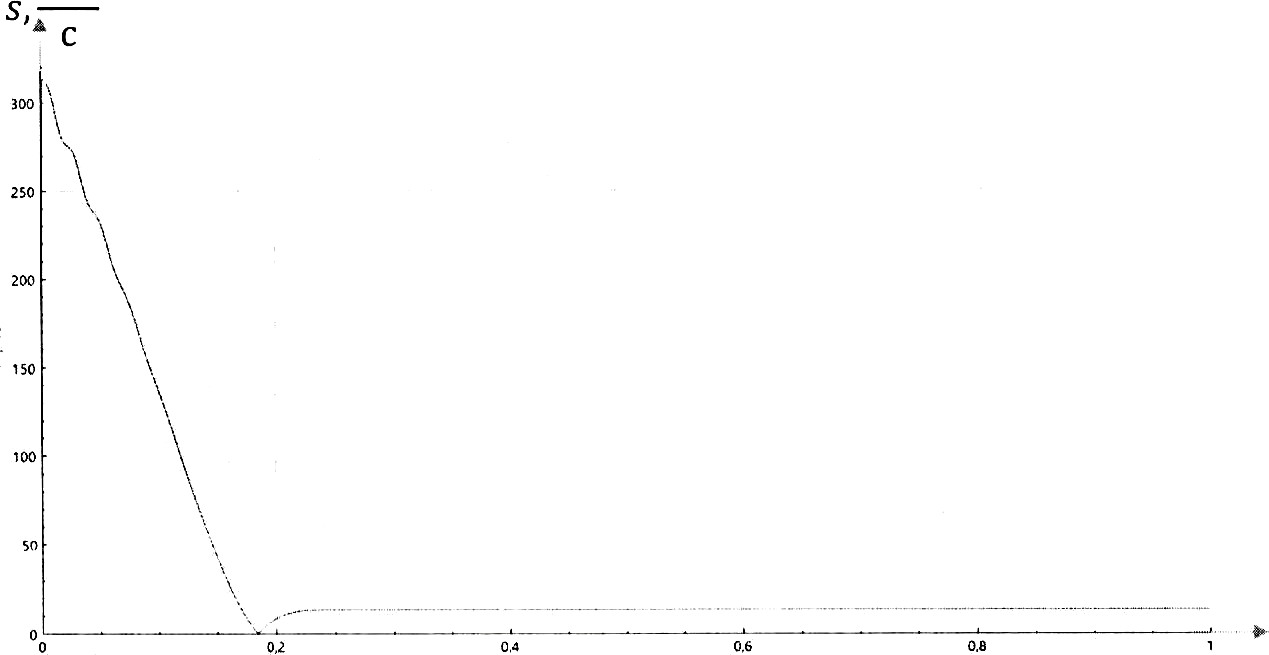t, c
Рис. 11. График изменения абсолютного скольжения асинхронной машины
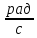
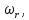
t t,c
Рис. 12 График изменения угловой скорости вращения ротора асинхронной машины
Выводы
На основе исследования режима работы асинхронного двигателя можно сделать следующие выводы:
1. Исследование работы асинхронного двигателя показывает, что основными факторами влияющим на устойчивость двигателя является его загрузка по активной мощности и значение внешнего сопротивления системы. Повышение этих показателей приводит к понижению запаса устойчивости.
2. Компенсация реактивной мощности оказывает благоприятное влияние на статическую устойчивость асинхронного двигателя.
З. При полной компенсации реактивной мощности (tan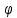
= 0) ухудшается динамическая устойчивость двигателя. Следовательно, в узлах где присутствуют асинхронные двигатели рекомендуется не полностью компенсировать реактивную мощность.
Построена векторная математическая модель частотного управления асинхронным электродвигателем. Данная модель позволяет моделировать переходные процессы механических характеристик асинхронный двигателей. В отличии от стандартной модели, реализованной в пакете Simulink, данная модель позволяет учитывать изменение параметров схемы замещения при изменении питающей сети. Простая реализация модели позволяет ее применять для исследования поведения асинхронных машин, перед их использованием в тех или иных режимах. На основе математической модели АД составлена программа для расчета механических характеристик при изменении частоты сети.
Список литературы
1. Акимов Л.В. Динамические параметры асинхронных двигателей частотно-регулируемых электроприводов / Л.В. Акимов, В.О. Котляров, Д.Г. Литвиненко// Электрические машины и аппараты. -2011.-№3.-с72
2.Булгаков А.А. Частотное управление асинхронными двигателями: Учебное пособие. СПБ: СПБ ГУ ИТМО,2006,-94с
3. Е.И. Визгина Математическая модель асинхронного двигателя большой мощности// Вестник Чувашского университета.- 2011.№3. –с.85.
4.Китаев В.Е. Электрические машины Ч II. Машины переменного тока: Учебное пособие. М.;Высш. школа, 1978.- 184с.
5.Усольцев А.А. Частное управление асинхронными двигателями : Учебное пособие. СПб: СПбГУ ИТМО, 2006,-94с
На рисунке 3 приведена разработка математической модели частотного регулирования. Согласно приведенной блок-схема (рис.3.) вычисление параметров схемы замещения приведена на рис. 4
Рис.3. Математическая модель частотного регулирования
Рис. 4. Вычисление параметров схемы замещения.
Выходными характеристиками математической модели являются угловая скорость вращения ротора
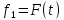и электромагнитный момент . Частота сети задается функцией от времени f = F(t). Функция приведена на рис 5. Рис. 5. График функции частоты тока сети от времени
На рисунке 6 приведен график угловой скорости вращения ротора
= F(t). График изменения момента асинхронной машины от времени = F(t) приведен на рисунке 7. Рис.6. График угловой скорости вращения ротора.
Рис.7. График изменения момента асинхронной машины
Для исследования асинхронного двигателя также удобна система
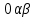ортогональных координат, неподвижных относительно статора. Это удобство объясняется тем
, что в такой системе все электромагнитные величины, связанные с осью
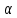, равны соответствующим величинам фазы А естественной системы[6]. Система дифференциальных уравнений асинхронного двигателя в неподвижной системы координат [6]: (18)г
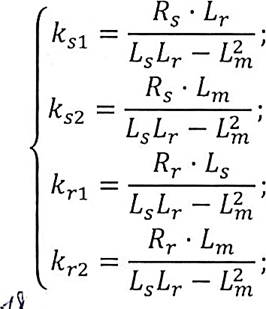
де
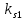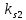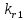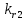, , , определяются из уравнений:Система уравнений (18) дает полную математическую модель АД. На основе вышеперечисленных уравнений методом Рунге-Кутта вычислим значения электромагнитного момента Мэ и угловую скорость вращения ротора
.Результаты расчетов получены программой блок- схема алгоритма работы программы для вычисления параметров асинхронного двигателя при разных значениях частоты питающей сети, приведена на рисунке 8. Подробный алгоритм работы программы приведен на рис 9.
Рис. 8. Блок-схема алгоритма работы программы для вычисления параметров асинхронного двигателя при разных значения частоты питающей сети.
Рис.9. Функция численного интегрирования
t,c
Рис.10. График изменения момента асинхронной машины
рад
t, cРис. 11. График изменения абсолютного скольжения асинхронной машины
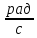
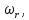
t t,c
Рис. 12 График изменения угловой скорости вращения ротора асинхронной машины
Выводы
На основе исследования режима работы асинхронного двигателя можно сделать следующие выводы:
1. Исследование работы асинхронного двигателя показывает, что основными факторами влияющим на устойчивость двигателя является его загрузка по активной мощности и значение внешнего сопротивления системы. Повышение этих показателей приводит к понижению запаса устойчивости.
2. Компенсация реактивной мощности оказывает благоприятное влияние на статическую устойчивость асинхронного двигателя.
З. При полной компенсации реактивной мощности (tan
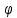= 0) ухудшается динамическая устойчивость двигателя. Следовательно, в узлах где присутствуют асинхронные двигатели рекомендуется не полностью компенсировать реактивную мощность.Построена векторная математическая модель частотного управления асинхронным электродвигателем. Данная модель позволяет моделировать переходные процессы механических характеристик асинхронный двигателей. В отличии от стандартной модели, реализованной в пакете Simulink, данная модель позволяет учитывать изменение параметров схемы замещения при изменении питающей сети. Простая реализация модели позволяет ее применять для исследования поведения асинхронных машин, перед их использованием в тех или иных режимах. На основе математической модели АД составлена программа для расчета механических характеристик при изменении частоты сети.
Список литературы
1. Акимов Л.В. Динамические параметры асинхронных двигателей частотно-регулируемых электроприводов / Л.В. Акимов, В.О. Котляров, Д.Г. Литвиненко// Электрические машины и аппараты. -2011.-№3.-с72
2.Булгаков А.А. Частотное управление асинхронными двигателями: Учебное пособие. СПБ: СПБ ГУ ИТМО,2006,-94с
3. Е.И. Визгина Математическая модель асинхронного двигателя большой мощности// Вестник Чувашского университета.- 2011.№3. –с.85.
4.Китаев В.Е. Электрические машины Ч II. Машины переменного тока: Учебное пособие. М.;Высш. школа, 1978.- 184с.
5.Усольцев А.А. Частное управление асинхронными двигателями : Учебное пособие. СПб: СПбГУ ИТМО, 2006,-94с