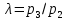Коэффициентом полезного действия (η) теплового двигателя называется отношение работы (W), производимой машиной за цикл, к количеству теплоты Q₁ получаемому машиной за этот цикл:

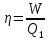
По первому началу термодинамики:


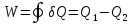
где Q₂ — абсолютное значение количества теплоты, отдаваемого рабочим телом за цикл, поэтому

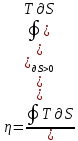
где 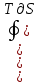берется по участкам цикла, на которых ∂S>0.

Для графического изображения процессов воспользуемся энтропийной диаграммой на плоскости с осями координат S, Т. На этой диаграмме величина 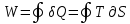равна площади цикла, а 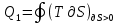определяет площадь, ограниченную предельными адиабатами 1А и ЗВ, осью абсцисс и элементами цикла с ∂S>0 (часть кривой цикла 1, 2, 3 на рис. 1).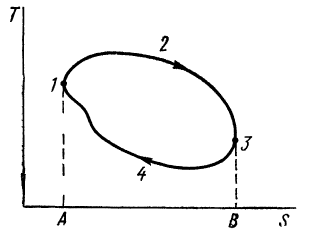



Рисунок 1

Рисунок 2

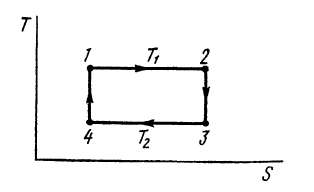
Вычислим КПД цикла Карно, состоящего из двух изотермических и двух адиабатных процессов. На диаграмме S, Т этот цикл изображен на рис. 2. На изотерме 1—2 теплота Q₁ берется от теплоотдатчика, на изотерме 3—4 теплота отдается тепло - приемнику. Эти теплоты и работа за цикл равны:
) , )


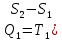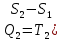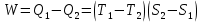
и, следовательно, КПД цикла Карно:

---

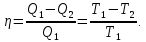
Отсюда видно, что КПД цикла Карно не зависит от природы рабочего вещества и предельных адиабат, а определяется только температурами теплоотдатчика и теплоприемника (первая теорема Карно). Из формулы (1) следует также, что влияние изменения температур Т₁ и Т₂ на значение КПД цикла Карно различно:



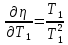
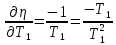
и так как T₁>T₂, то 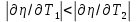. Таким образом, изменение температуры теплоотдатчика в меньшей степени влияет на изменение КПД цикла Карно, чем изменение температуры тепло - приемника.

Чем ниже температура Т₂ теплоприемника при данной температуре Т₁ теплоотдатчика, тем выше КПД цикла Карно. Однако цикл Карно с температурой Т₂ теплоприемника, равной 0 К, осуществить невозможно, так как это противоречило бы второму началу термодинамики (теплота Q₁, взятая у нагревателя, в таком цикле полностью превращалась бы в работу). Невозможность по второму началу цикла Карно с температурой теплоприемника Т₂ =0 К выражается не в том, что 0 К недостижим (этот вопрос не решается вторым началом), а в том, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм . Таким образом, второму началу не противоречит достижение 0 К, но цикл Карно с температурой теплоприемника T₂ =0 К невозможен.

По этой причине порочны все выводы и доказательства, основывающиеся на использовании и анализе цикла Карно с T₂=0 К. Например, неверным является утверждение о том, что для осуществления полного превращения теплоты в работу с помощью периодически действующей тепловой машины надо было бы располагать холодильником, температура которого равна 0 К, и что, поскольку такого холодильника нет, периодически действующая машина может превращать в работу только часть теплоты. В действительности же даже при наличии холодильника с температурой 0 К вечный двигатель второго рода невозможен, так как при

---

T₂=0 К цикл Карно вырождается.

Как устанавливает третье начало термодинамики, 0 К недостижим, и поэтому цикл Карно с температурой холодильника T₂=0 К осуществить тем более невозможно.

Заметим, что, допуская возможность цикла Карно с температурой холодильника T₂=0 К, можно прийти к неверному выводу о том, что уже по второму началу изотермический процесс при 0 К одновременно является и адиабатным. В самом деле, предполагая, что цикл Карно с T₂=0 К осуществим, из формулы (1) получаем:

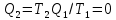
в то время как из второго начала этот вывод без дополнительных предположений не следует.

Действительно, при элементарном изотермическом изменении какого-либо параметра х по второму началу имеем:

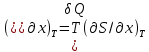
Отсюда видно, что если при T→0 К производная 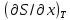изменится по закону 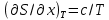, где с = const, то изотермический процесс при температуре T = 0 К не будет адиабатным, если же 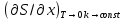то изотермический процесс при температуре T = 0 К будет адиабатным. Сказать, как изменяется S при различных процессах, когда T→0 К, второе начало ничего не может, и поэтому нельзя утверждать, что уже по второму началу все процессы при 0 К являются адиабатными. К такому выводу можно прийти или в результате неверного предположения о возможности цикла Карно с T₂ = 0 К, или при дополнительном предположении, что изменение энтропии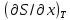

---

при 0 К конечно, хотя и отлично от нуля. По третьему началу поэтому нулевая изотерма совпадает с нулевой изоэнтропой, а следовательно, и с адиабатой.

Теорема Карно указывает путь повышения КПД тепловых машин. Она сыграла руководящую роль в развитии основ теплотехники. Хотя ни одна применяемая в технике тепловая машина не работает по циклу Карно, значение этого цикла состоит в том, что он имеет наибольший КПД по сравнению с циклами, работающими в тех же температурных пределах, и является мерой КПД всех других циклов.

Если машина при заданных внешних условиях работает по некоторому циклу и получает при необратимом цикле то же количество теплоты Q₁, что и при обратимом, то, поскольку работа W_нр за необратимый цикл меньше работы W обратимого цикла КПД необратимой машины 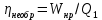меньше КПД обратимой машины 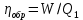(вторая теорема Карно):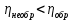


Проблема промышленной выработки электроэнергии является одной из важнейших задач развития экономики. В настоящее время основную часть электроэнергии ( — 80%) вырабатывают паротурбинные электростанции и около 20% — гидроэлектростанции. В турбинах внутренняя энергия топлива вначале преобразуется в механическую энергию вращения, а потом в генераторах в электрическую энергию. Такое двухступенчатое преобразование теплоты в электроэнергию, связанное с использованием быстро- движущихся частей, не позволяет повысить температуру пара выше 600—650°С, вследствие чего КПД паротурбинных электростанций не превосходит 40—42%. Поэтому уже давж> ведутся исследования прямого (безмашинного) преобразования внутренней энергии в электроэнергию.

В настоящее время наибольшее научно-техническое развитие получил магнитогидродинамический метод (МГД-метод) прямого преобразования энергии. Идея этого метода основана на том, что при пересечении проводником линий индукции в нем возникает ЭДС. В МГД-генераторе таким проводником является электропроводящий газ (плазма). Высокотемпературный газ (2500— 3000°С) в МГД-генераторе выполняет двойную роль: в сопле перед генератором внутренняя энергия газа преобразуется в кинетическую энергию потока, т. е. газ является термодинамическим рабочим телом, а в генераторе кинетическая энергия потока преобразуется в электрическую энергию, т. е. газ выполняет роль силовой обмотки электрической машины. Можно поэтому говорить, что МГД-генератор представляет собой совмещенную с тепловым двигателем электрическую машину, а термодинамический цикл энергетической установки с МГД-генератором принципиально ничем не отличается от известных циклов газо- и паротурбинных установок. Использование высокой температуры рабочего вещества (которую вполне выдерживают неподвижные части генератора) приводит к генерации электроэнергии МГД-методом с КПД до 50-60%.

---

Цикл Рейтлингера - обобщённый замкнутый Термодинамический цикл теплового двигателя или холодильной установки с регенерацией теплоты. Так же как и цикл Карно позволяет достигать максимума подводимой в цикле теплоты при заданной экстремальной температуре цикла. Термодинамический КПД Цикла Рейтлингера равен КПД Цикла Карно. Цикл состоит из двух изотермических процессов и двух политропных процессов.

Рабочее тело в ходе цикла:

1. 
   сжимается в политропном процессе с одновременным получением тепла из регенератора, показатель политропы n≠1;
   
2. 
   расширяется в изотермическом процессе с одновременным получением тепла от нагревателя, показатель политропы n=1;
   
3. 
   расширяется в политропном процессе с одновременной отдачей тепла регенератору, показатель политропы n≠1;
   
4. 
   сжимается в изотермическом процессе с одновременной отдачей тепла холодильнику, показатель политропы n=1.
   

В наиболее известных регенеративных циклах:

• 
  Цикл Стирлинга показатель политропы n=∞, т.е. регенеративный теплообмен осуществляется при постоянном объёме (Изохорный процесс);
  
• 
  Цикл Эрикссона пользуется показатель политропы n=0, и его регенератор работает при постоянном давлении (Изобарный процесс).
  

Цикл Ха́мфри (Humphrey. В русской транскрипции также пишут Гэмфри или Гемфри) — термодинамический цикл, описывающий рабочий процесс клапанного пульсирующего воздушно-реактивного двигателя

Идеальный цикл Хамфри состоит из процессов:

• 
  1—2 адиабатическое (изоэнтропийное) сжатие рабочего тела за счёт напора встречного потока воздуха (при открытом клапане):
  
• 
  2—3 изохорический нагрев при сгорании топлива в замкнутом объёме (при закрытом клапане):
  
• 
  3—4 адиабатическое расширение;
  
• 
  4—1 изобарическое (при постоянном давлении) охлаждение.
  

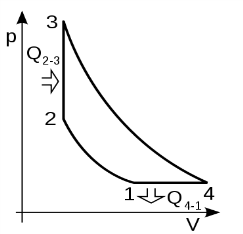
Рисунок 3
Термический коэффициент полезного действия цикла может быть выражен уравнением:


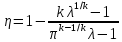
Здесь k - показатель адиабаты, 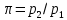— степень повышения давления в адиабатическом процессе 1—2,

---

Смотрите также файлы

• Образом выбранный нами инновационный путь требует от нас анализа модели развития.docx

• Название района.docx

• Общая часть Характеристика, назначение и классификация грузовых станций Специальная часть.docx

• Человек и общество.docx

• Пояснительная записка курсовой работы по дисциплине гтм Проект гидротехнических мероприятий с элементами ландшафтного дизайна на территории садовопаркового участка Смоленской области.docx