Файл: Решение По формуле, где f наращенная сумма p вложенная сумма r.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 30.11.2023
Просмотров: 636
Скачиваний: 30
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа Анализ денежных потоков
Вариант 3
-
В финансовом договоре клиента с банком предусмотрено погашение долга в размере 250 тыс. руб. через 180 дней при взятом кредите в 200 тыс. руб. Определите доходность такой операции для банка, если банк использует простые обыкновенные проценты.
Решение:
По формуле:
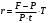 , где
, гдеF – наращенная сумма;
P – вложенная сумма;
r – простая процентная ставка;
t – продолжительность финансовой операции в днях;
Т – количество дней в году.
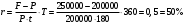
Ответ: 50% годовых.
2)Банк за 20 дней до срока погашения учел вексель на сумму 40 тыс. руб. Доход банка составил 800 руб. Какую простую учетную ставку использовал банк, если считать в году 360 дней?
Решение:
По формуле:
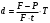 ,где
,гдеd – простая учетная ставка;
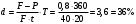
Ответ: 36%.
3)Клиент поместил 500 тыс. руб. в банк на 2 года под процентную ставку 10% годовых. Определите наращенную за это время сумму при начислении сложных процентов: а) ежегодно; б) ежеквартально; в) ежемесячно.
Решение:
S=P(1+
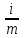 )n*m
)n*mГде: S – наращенная сумма; Р – первоначальная сумма на которую начисляется процент; i – номинальная годовая процентная ставка, выраженная десятичной дробью; n – число лет; m – число периодов начисления процентов в течение года; n*m – число периодов начисления процентов за весь срок контракта
а) Ежегодное начисление процентов:
S = 500000(1+0,1)2=605000 руб.
б) Ежеквартальное начисление процентов:
S = 500000 (1+
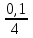 )2*4=609201 руб.
)2*4=609201 руб.в) Ежемесячное начисление процентов:
S = 500000 (1+
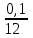 )2*12=609712 руб.
)2*12=609712 руб.4)В банк 5 июля предъявлен для учета вексель на сумму 200 тыс. руб. со сроком погашения 5 сентября того же года. Банк учитывает вексель по сложной учетной ставке 20% годовых, считая год равным 360 дней и проводя приблизительный подсчет дней. Определить сумму, которую получит векселедержатель, и доход банка.
Решение:
P=F· (1 –d)n,
при F= 200 000;d= 0,2;n= 60/ 360,
Р = 200 000 · (1 – 0,2)0,17=192600 руб.
D=F–P,
D =200 000 – 192 600 = 7400 руб.
Сумма, которую получит векселедержатель192 698,5 руб.
Доход банка 7400 руб.
5) Банк учитывает вексель по простой учетной ставке 22% годовых. Какой величины должна быть сложная учетная ставка с ежемесячным учетом, чтобы доход банка при учете векселя не изменился?
Решение:
J=m
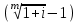 ,
,где: J - сложная учетная ставка, m – число периодов учета, I – простая учетная ставка
j = 12(
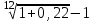 ) = 0,2005 или 20%
) = 0,2005 или 20%6) Два векселя: один номинальной стоимостью 20 000 руб. и сроком погашения 10 июня; другой номинальной стоимостью 50 000 руб. и сроком погашения 1 августа заменяются одним с продлением срока погашения до 1 октября. Определить номинальную стоимость нового векселя при использовании простой учетной ставки 8% годовых.
Решение:
Поскольку срок погашения нового векселя позже, чем сроки погашения объединяемых векселей, то на сумму 20 000 руб. в течении 113 дней (с 10 июня по 1 октября) происходит наращение капитала по простой учетной ставке 8%; на сумму 50 000 руб. в течении 61 дней (с 1 августа по 1 октября) также происходит наращение капитала по простой учетной ставке 8% годовых. Поэтому номинальная стоимость нового векселя равна:
F = 20000 · (1 – 113 / 360)-1 + 50000 · (1 – 61 / 360)-1 = 89 347, 72 руб.
7) На некоторую сумму, помещенную на депозит в банк, в течение 4-х лет будут начисляться непрерывные проценты. По прогнозам инфляция в это время каждый год будет составлять 6%, 7%, 8% и 9%. Какова должна быть сила роста за год, чтобы сумма вклада через четыре года по своей покупательной способности не уменьшилась?
Решение:
Представим, что х- размет вклада. Через 4 года, с учетом инфляции, эта сумма превратится в:
S4=
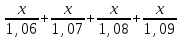
Пусть m – сила роста за 1 год, тогда:
x-m4>
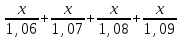
Разделим на х:
m4>
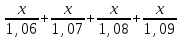
m4>
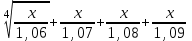 >1,44 следовательно, нужен прирост более 144% в год
>1,44 следовательно, нужен прирост более 144% в годОтвет: 144%
8) В банк на депозит внесено 5000 долл., срок депозита — три года, сложная ссудная ставка равна 9% годовых. Ставка налога на начисленные проценты равна 3%. Определить
наращенную сумму с учетом налога на проценты, сумму уплаченного налога и реальную доходность финансовой операции.
Решение:
F=P(1+r*n), где
t - ставка налога на проценты
N – общая сумма налога
F- наращенная сумма до выплаты налога на проценты
Ft - наращенная сумма после выплаты налога на проценты
P – вложенная сумма
n – продолжительность финансовой операции
r - сложные ссудные проценты
F = 5000(1+0,09*3)=6350
N=(F - P) t
N=(6350-5000)0,03=40,5
Ft =F – N
Ft=6350-40,5=6309,5
9) Раз в квартал делается взнос в банк по схеме постнумерандо в размере 400 долл. Банк ежемесячно начисляет сложные проценты по ставке 5% годовых. Какая сумма будет на счете через 6 лет?
Решение:
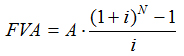
где A – размер платежа;
i – процентная ставка за период;
N – количество периодов.
А=400; N = 24 (6 лет по 4 платежа)
FVA=400*((1+0,004167)24-1)/0,004167=10074,41у.е.
10) Какую сумму необходимо поместить в банк под сложную процентную ставку 8% годовых, чтобы в течение 5 лет иметь возможность в конце каждого года снимать со счета 300 тыс. руб., исчерпав счет полностью, при следующих условиях: 1) банк начисляет сложные проценты ежеквартально; 2) банк начисляет сложные проценты ежемесячно?
Решение: При нахождении искомой суммы во всех случаях необходимо определить приведенную стоимость Р-срочного аннуитета постнумерандо при Р=1,
А=300 тыс. руб., n=5.
-
При начислении процентов по кварталам m=4, mn=4*5=20, r/m=8%/4=2%, m/p=4/1=4
PVpst=A
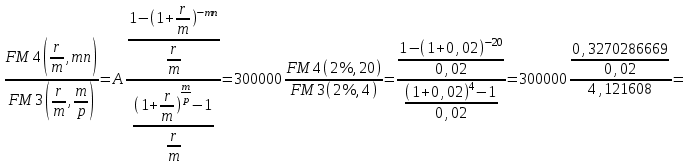
=300000*3,967=1190100 руб..
-
2) При начислении сложных процентов ежемесячно m=12, mn=12*5=60, r/m=8%/12=0,6667 %, m/p=12/1=12
PVpst=A
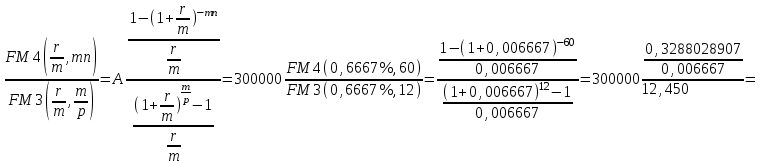
= 300000*3,961=1188300 руб.
11) Вам необходимо накопить 25 тыс. долл. за 8 лет. Каким должен быть ежегодный взнос в банк (схема пренумерандо), если банк предлагает 10% годовых. Какую сумму нужно было бы единовременно положить в банк сегодня, чтобы достичь той же цели?
Решение
Будущая стоимость постоянного аннуитета пренумерандо определяеся по формуле:
где А – искомый ежегодный взнос в банк, r=0,1 – процентная ставка (10%), n=8лет.
Подставляем известные данные:
25000 = A*FM3(10%,8)*(1+0,1)
25000 = А*11,436*1,1
А = 1987 (долл.).
Если денежный поток представляет собой регулярные начисления процентов на вложенный капитал по схеме сложных процентов, то в основе оценки наращенного денежного потока лежит формула нахождения будущей стоимости:
FV=PV*(1+r)n
25000 = РV * (1+0,1)8
PV = 11663 (долл.).
Ответ: 11663 (долл.).
12) Некоторая фирма создала фонд в размере 10 млн руб. для премирования
своих работников. Фирма предполагает ежегодно выплачивать работникам
1 млн руб. Найти срок использования фонда, если банк начисляет ежегодно
сложные проценты по ставке 6% годовых.
Решение
Поток ежегодных выплат из фонда представляет собой аннуитет, срок которого можно выразить по формуле: , где PVpst =10 млн.руб. – приведенная стоимость аннуитета, r=0.06 – процентная ставка (6%), А=1 млн.руб. – периодические денежные платежи. n=-ln1-101*0.06ln1+0.06=15.7 (лет). Ответ. Срок использования фонда 15,7 лет.
13) Какую сумму необходимо положить на депозит, чтобы в течение 15 лет
снимать со счета в начале каждого года по 10 тыс. долл., если банк начисляет проценты по сложной учетной ставке 8% годовых? Как изменится
ответ, если банк будет начислять проценты по сложной ссудной ставке 8%
годовых?
Решение
Формула для нахождения приведенной стоимости аннуитета пренумерандо по сложной ссудной ставке:
,
где r - ссудная ставка, А – постоянный платеж.
Для перехода к эквивалентной учетной ставке воспользуемся формулой:
d=r1+r,
где d - учетная ставка.
Формула для нахождения приведенной стоимости аннуитета пренумерандо по сложной ссудной ставке:
PVpre=A*FM4r1+r,n*(1+r1+r).
Приведенная стоимость по сложной учетной ставке:
PVpre=10000*FM40,081+0,08,15*1+0,081+0,08=10000*FM47,4%,15*1,074=10000*8,9*1,074=95586 (руб.).
Приведенная стоимость по сложной ссудной ставке:
PVpre=10000*FM48%,15*1+0,08=10000*8,560*1,08=92448 (руб.).
Ответ : 95586 руб, 92448 руб
14) Необходимо выкупить полугодовую ренту с платежами в 50 тыс. руб., срок
ренты — 10 лет; сложные проценты по ставке 10% начисляются по полугодиям. Определить сумму выкупа ренты.
15) За 5 лет необходимо накопитъ 2 млн руб. Какой величины должен быть
первый вклад, если предполагается каждый год увеличивать величину денежного поступления на 200 тыс. руб. и процентная ставка равна 8% годовых? Денежные поступления осуществляются в начале каждого года.
Решение
Воспользуемся формулой для оценки будущей стоимости аннуитета пренумерандо: FV = (A + z / r)FM3(r,n) –zn / r, при FV = 2000000; z = 200; r = 0,08; n = 5 А = (2000000 + 0,08 * 5 * 200) / FM3(8%,5) – 200/0,08 = 2000080/1+0,085-10,08- 2500 =337 939 руб. Ответ: величина первого вклада равна 337 939 руб.
16) Месторождение полезных ископаемых будет разрабатываться в течение 8
лет, при этом ожидается, что доходы от эксплуатации месторождения составят в среднем 300 млн руб. в год. Определите приведенную стоимость
ожидаемого дохода при использовании сложной процентной ставки 10%
годовых и в предположении, что отгрузка и реализация продукции будут
непрерывны и равномерны.
Решение
В условии говорится о равномерной отгрузке и реализации продукции в течение года, поэтому интенсивность потока выручки будет постоянной величиной, равной 300 млн . руб. в год. Считая, что денежные поступления происходят непрерывно, воспользуемся формулой для определения приведенной стоимости аннуитета при непрерывном поступлении платежей и непрерывном начислении процентов:
,
где А – постоянная сумма доходов, - процентная ставка, n – количество лет.
PV=300*1-e-0.1*80.1=1652 (млн.руб.).
Ответ
. руб. в год. Считая, что денежные поступления происходят непрерывно, воспользуемся формулой для определения приведенной стоимости аннуитета при непрерывном поступлении платежей и непрерывном начислении процентов:
,
где А – постоянная сумма доходов, - процентная ставка, n – количество лет.
PV=300*1-e-0.1*80.1=1652 (млн.руб.).
Ответ: 1652 (млн.руб.).
17) Определить текущую (приведенную) стоимость бессрочного аннуитета
постнумерандо с ежемесячными поступлениями в сумме 10 тыс. руб., если предлагаемый государственным банком процент по срочным вкладам
равен 14% годовых, начисляемых ежеквартально.
Решение
Приведенная стоимость бессрочного аннуитета постнумерандо с денежными поступлениями p=12 раз за базовый период и начислением сложных процентов m=4 раз за базовый период определяется по формуле: . PVpst=100001+0,144412-1=867066 (руб.). Ответ. Текущая стоимость бессрочного аннуитета 867066 руб.
18) Определить сумму, которую необходимо поместить на счет в банке, чтобы
в течение 16 лет в конце каждого двухлетнего периода иметь возможность
снимать со счета 100 тыс. руб. и концу срока снять все деньги со счета,
если банк начисляет на вклады 1) ежегодно сложные проценты по ставке
8% годовых; 2) ежеквартально сложные проценты по ставке 8% годовых;
3) непрерывные проценты с силой роста 8% годовых.
Решение
Во всех случаях надо определить приведенную стоимость постоянного аннуитета с A = 100 тыс. руб., периодом u = 2 года и сроком n = 16 лет: