Регрессиялық талдау.

Айталық, бізде және екі параметрдің n мәндер жұбы бар болсын. Яғни, бір ғана объектінің екі параметрі өлшенген. Осы параметрлердің арасында қандай да бір мәнді байланыс бар ма деген сұраққа жауап беру керек.

және кездейсоқ шамалары өзара тәуелді немесе тәуелсіз болуы мүмкін. Тәуелділіктің екі түрі бар: функционалдық және статистикалық. Математикада айнымалысының айнымалысынан функционалдық тәуелділігі деп - тің әрбір мүмкін мәніне қандай бір белгілі ереже бойынша - тің бір ғана мүмкін мәні сәйкес қойылатын түріндегі тәуелділікті айтады.

Алайда, егер және кездейсоқ шамалар болса, онда олардың арасында статистикалық деп аталатын тәуелділіктің басқа түрі болуы мүмкін. және кездейсоқ шамаларының мәндерінің қалыптасуына әртүрлі факторлар әсер етеді. Осы факторлардың әсер етуі нәтижесінде және нақты мәндері қалыптасады. Айталық, және - ке бірдей факторлар, мысалы әсер етсін, онда және бір-бірімен толық сәйкестікте болады және функционалды байланысады. Енді айталық, Х – ке , ал -ке тек қана және факторлары әсер ететін болсын. және екеуі де кездейсоқ шамалар, бірақ олардың екеуіне бірдей әсер ететін және ортақ факторлары бар болғандықтан, олар өзара байланысты және бұл байланыс функционалдыбола алмайды, себебі: кездейсоқ шамалардың біреуіне ғана әсер ететін факторы және мәндерінің арасындағы тікелей (функционалдық) тәуелділікті бұзады. Бұл жағдайдағы байланыс сынаудан сынауға дейін өзгеріп отыратын кездейсоқ байланыс. Мұндай байланысты статистикалық деп атайды. Бұл жағдайда - тің әрбір мәніне функционалдық тәуелділіктегі сияқты - тің бір ғана мәні емес, қандай да бір мәндер жиыны сәйкес келуі мүмкін.

Анықтама 1. Егер бір кездейсоқ шаманың өзгеруіне екінші кездейсоқ шаманың таралу заңының өзгеруі сәйкес келсе, онда олардың арасындағы тәуелділік статистикалық деп аталады.

Анықтама 2. Егер бір кездейсоқ шаманың өзгеруіне екінші кездейсоқ шаманың орта мәнінің өзгеруі сәйкес келсе, онда олардың арасындағы статистикалық тәуелділік корреляциялық деп аталады.

Корреляциялық тәуелділікпен байланысқан кездейсоқ шамаларды корреляцияланған деп атайды.

Корреляциялық тәуелділіктің мысалдары: дененің салмағымен бойдың ұзындығының арасындағы тәуелділік: бойдың ұзындығының (Х) әрбір мәніне дене салмағының ( ) мәндер жиыны сәйкес келеді.

• сыртқы факторлардың әсері мен аурудың арасындағы тәуелділік, мысалы, ауаның шаң – тозаңдығы, радиация деңгейі, күн көзінің өтімділігі және т. б.;

• аңдардың салмағы мен олардың қандарындағы гемоглобиннің мөлшері арасындағы тәуелділік;

• объектіге егілген препараттың мөлшерімен оның қандағы ерітіндісінің арасындағы тәуелділік;

Сол сияқты корреляция

• ионданған сәуле шығару дозасы мен мутация санының арасында;

• адам шашының пигменті мен көзінің түсі арасында;

• студенттердің жіберген дәрістері мен емтихандағы бағаларының

---

арасында бар.

Табиғатта ең жиі кездесетін тәуелділік – ол корреляциялық тәуелділік. Себебі зерттеліп отырған көрсеткіштерді анықтайтын өте көп әртүрлі факторлар бір-біріне әсер ету арқылы әрдайым байланыста болады.

1. Корреляциялық тәуелділік

- тің - ке тәуелділігін

(1)

түріндегі теңдеу арқылы сипаттауға болады, мұндағы - Х шамасының мәніне сәйкес келетін шамасының шартты орта мәні, ал - қандай да бір функция. (1) теңдеу - тің - ке таңдама регрессия теңдеуі деп аталады.

функциясын - тің - ке таңдама регрессиясы деп, ал оның графигін - тің - ке регрессиясының таңдама сызығы деп атайды.

Дәл осы сияқты - тің - ке регрессиясының таңдама теңдеуі түрінде болады.

Регрессия теңдеуінің түріне және оған сәйкес сызықтық түріне байланысты қарастырылып отырған шамалардың арасындағы корреляциялық тәуелділіктің түрін анықтайды. Ол – сызықты, квадратты, көрсеткіштік болуы мүмкін.

[немесе ] регрессия функциясының түрін таңдап алу – маңызды сұрақ болып табылады. Мысалы, сызықты немесе сызықты емес (көрсеткіштік, квадраттық, логарифмдік және т.б.)

Практикада регрессия функциясының түрін координата жазықтығында бақылаудың ( ) мәндер жұбының барлығына сәйкес келетін нүктелер жиынын тұрғызу арқылы анықтауға болады.

0. Сызықтық регрессия

Регрессия функциясының, яғни - тің - ке (немесе - тің - ке) тәуелділігінің моделінің түрін таңдап алғаннан кейін, мәселен, сызықтық моделін, моделдің коэффициенттерінің нақты мәндерін анықтау қажет.

және әртүрлі мәндері бойынша түріндегі шексіз көп тәуелділікті алуға болады, яғни координата жазықтығындағы шексіз көп түзулер тұрғызуға болады, ал бізге бақылап отырған мәндерге өте жақын, ең тиімді түрде сәйкес келетін тәуелділік қажет. Яғни, ең жақсы коэффициенттерді таңдау керек.

Ең кіші квадраттар әдісі (ЕКӘ)

сызықтық функциясын бақылау нәтижесінде алынған мәндерге қатысты іздейміз. Бақылау мәндеріне өте жақын сәйкес келетін функцияны табу үшін ең кіші квадраттар әдісін қолданамыз.

Мынадай белгілеулер енгіземіз: - теңдеуі бойынша есептелінген мәндер,

- бақылау нәтижесінде өлшелініп алынған мәндер,

- өлшелініп алынған мәндер мен теңдеу бойынша есептелінген мәндердің айырмасы, .

Ең кіші квадраттар әдісінде өлшелініп алынған мәндері мен теңдеу бойынша есептелінген мәндерінің айырмасы ең аз (минимальды) болуы талап етіледі. Яғни, а және коэффициенттерін бақылап отырған мәндердің түзу сызықты регрессияның мәндерінен ауытқуының квадраттарының қосындысы өте аз болатындай етіп іздейміз:

.

Бұл - фукнкциясы а және аргументтеріне тәуелді екі айнымалының функциясы болып табылады. - функциясын туындының көмегі арқылы экстремумға зерттей отырып, бұл функция минимальды мәнді, егер а және коэффициенттері мынадай жүйенің шешімі болған жағдайда қабылдайтынын дәлелдеуге болады.

---

(*)

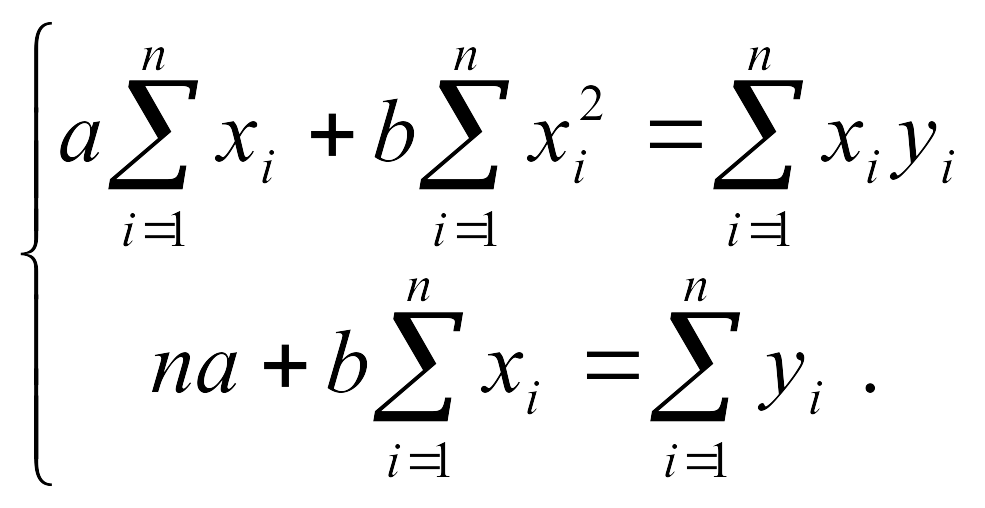Бұл жүйе ең кіші квадраттар әдісінің қалыпты теңдеулер жүйесі деп аталады.

Егер қалыпты теңдеулердің екі жағын да n – ге бөлсек, онда

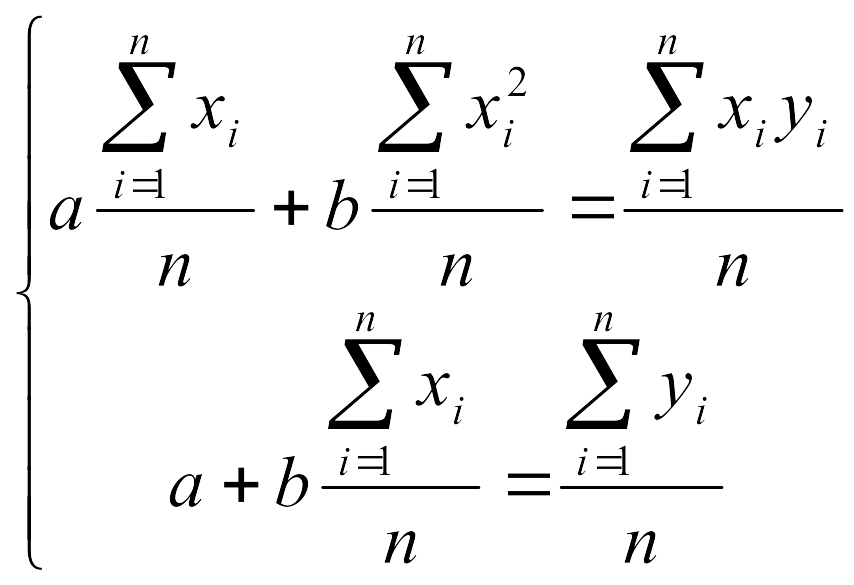
аламыз.

, (**)

екенін ескерсек,

аламыз. Бұдан , а- ның мәнін бірінші теңдеуге қою арқылы

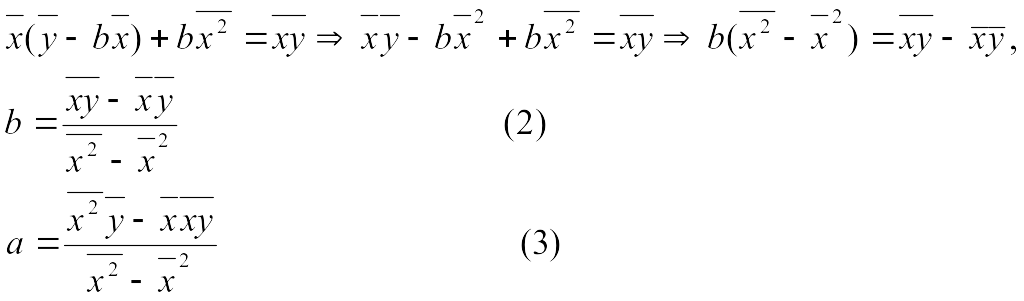
аламыз. - регрессия коэффициенті, а- регрессия теңдеуінің бос мүшесі.

Алынған түзу теориялық регрессия сызығының бағасы болып табылады.

.

Сонымен, сызықтық регрессияның теңдеуі.

Регрессия тура және кері болуы мүмкін.

Егер бірінші параметрдің мәндері өскенде, екінші параметрдің мәндері өсетін болса, онда ол тура регрессия, ал бір параметрдің мәндері өскенде, екінші параметрдің мәндері кемитін болса, онда ол – кері регрессияны білдіреді.

1-мысал. n елді мекендерінде тәулігіне тұщы суды санитарлы-тұрмыстық мұқтаждыққа пайдаланудың Х (л/адам) берілген деңгейіне жалпы ауру-сырқаулықтың (%) деңгейінің көптеген мәні сәйкес келеді. (% - ке шаққанда). Бұл жағдайда Х-тің өсуіне - ң кемуі сәйкес келетіні байқалады. Бұл – кері, теріс корреляциялық байланыс. (1 сурет).

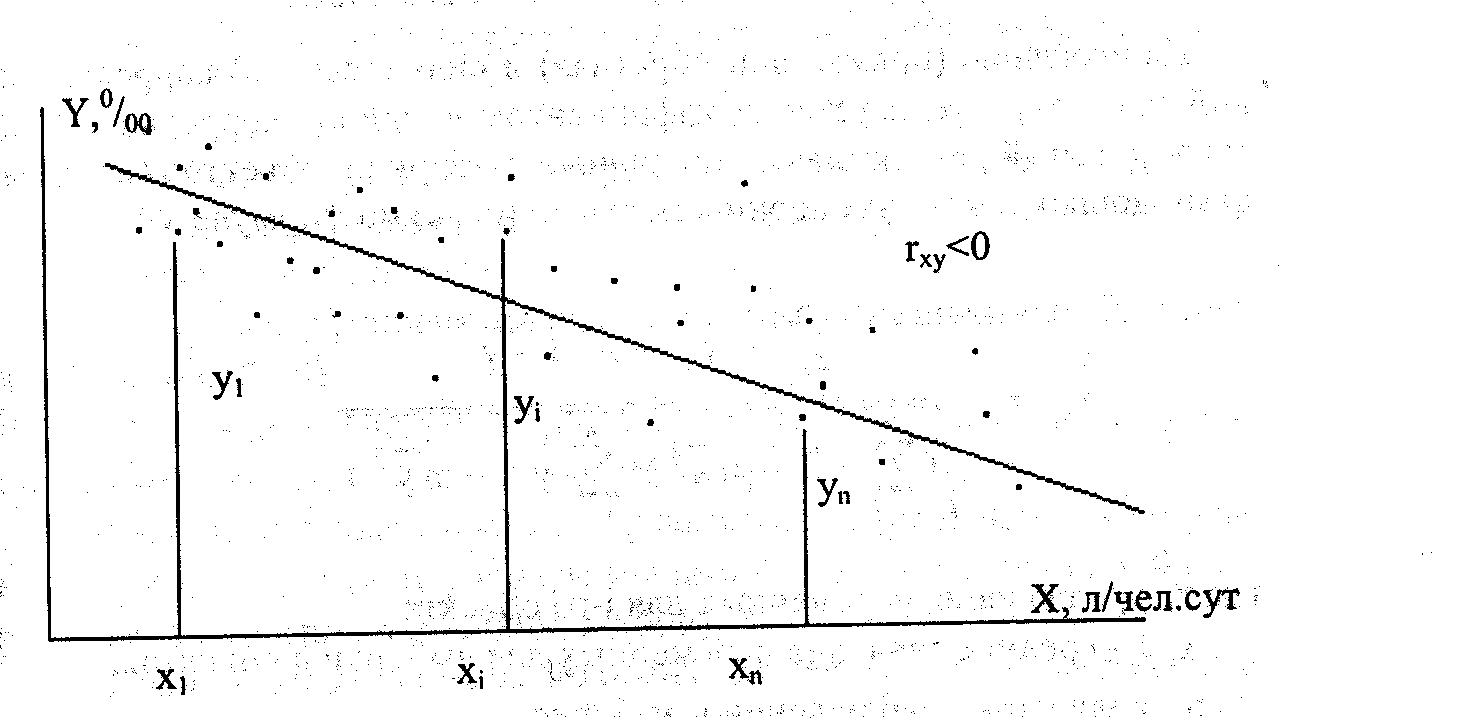
1-сурет. Х факторы мен параметрінің арасындағы кері корреляциялық байланысты бақылау өрісі.

2
-мысал. Өндіріс аймағындағы жұмыс орнының тығыздығы Х (адам) өскен сайын жұқпалы ауру деңгейінің (% пен) өсуі – тура, оң корреляциялық байланыстың мысалы болып табылады (2 сурет).

2-сурет. Х факторы мен параметрінің арасындағы тура корреляциялық байланысты бақылау өрісі.

Регрессия коэффициентінің мәнділігі туралы жорамалды тексеру

Біз бақылау нәтижесінде алынған өлшемдерді сипаттайтын модельді алдық, енді оның дұрыс екендігін анықтау керек.

Регрессиялық талдаудың моделі: мұндағы түрінде болады. - бойынша ығысуды сипаттайтын параметр, - регрессия коэффициенті, функция графигінің Х бойынша ығысуын сипаттайтын параметр, - кездейсоқ айнымалының корреляциялық тәуелділікпен байланыспаған (коррелденбеген) қателіктері.

Регрессиялық талдауда регрессия коэффициентінің және бос мүшесінің мәнділігі туралы жорамалды тексереді.

1. және жорамалдарын анықтаймыз.

: (айнымалылар арасында сызықтық тәуелділік жоқ)

: .

2. мәнділік деңгейін береміз.

3. Критерийдің статистикасы

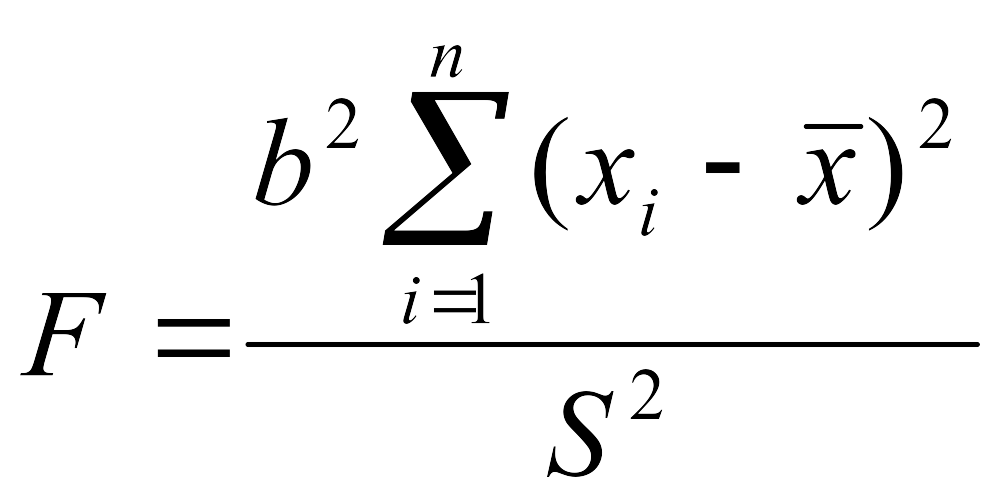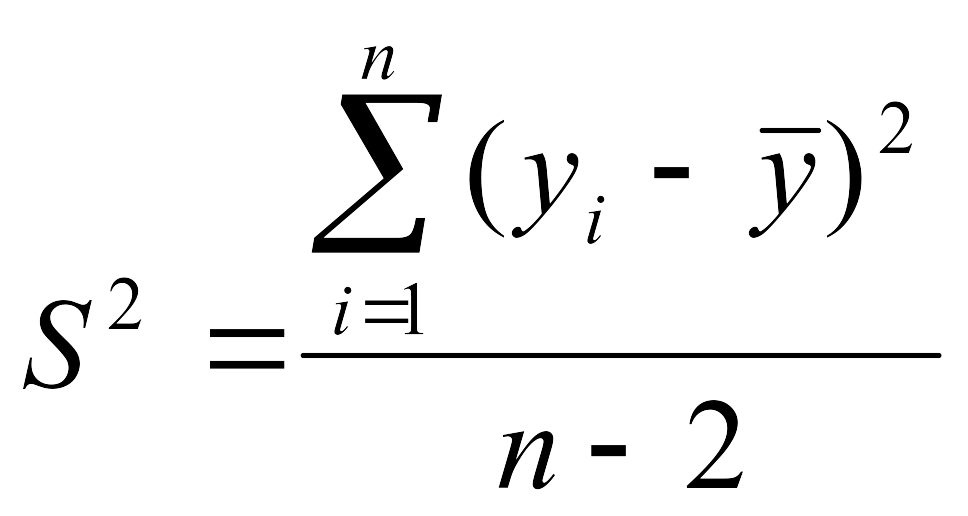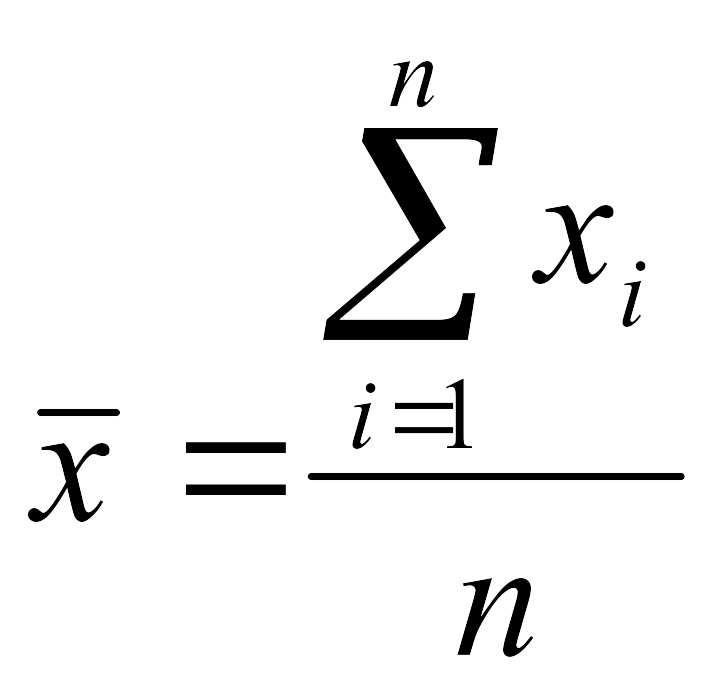, мұндағы , және .

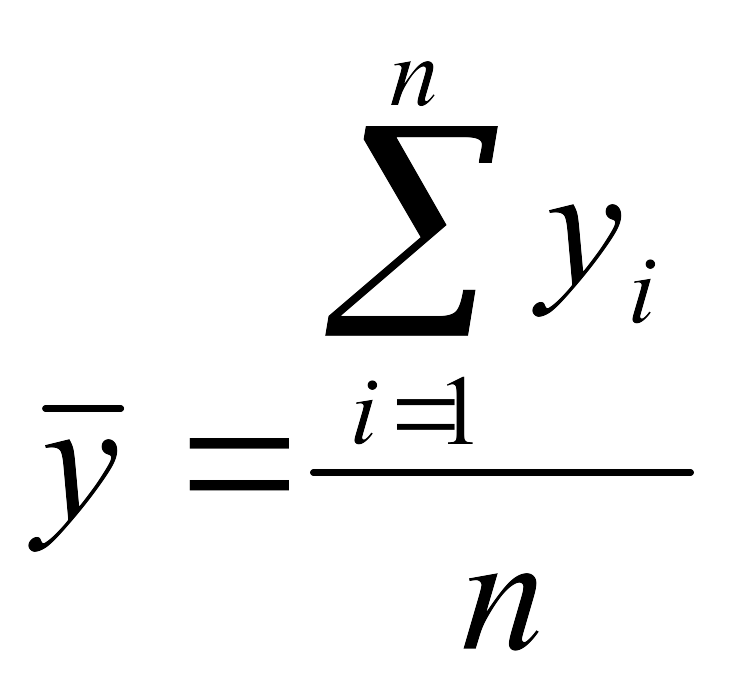4. Критикалық нүктелер және критикалық аймақ . F статистикасы 1 және (n-2) бос дәрежелерімен Фишер таралуына тең.

5. Егер , онда Н₀ теріске шығарылады, яғни сызықтық тәуелділік мәнді деген қорытынды жасауға болады.

Егер , онда бізде Н₀- ді қабылдамауға негіз жоқ, яғни сызықтық тәуелділік – мәнді емес немесе берілгендерді сызықтық регрессия моделімен сипаттауға болмайды.

Сызықтық корреляция.

Корреляциялық талдау.

Корреляциялық талдау Х және кездейсоқ шамаларының арасындағы байланыстың дәрежесін анықтаумен айналысады.

Екі кездейсоқ шамалар үшін тәжірибе нәтижесінде алынған деректердің корреляциялық талдауы мынадай негізгі тәсілдерді қарастырады:

---

1. Корреляциялық таңдама коэффициентін есептеу.

2. Корреляциялық кесте құру.

3. Байланыс мәнділігі жөніндегі статистикалық жорамалды тексеру.

Анықтама. Егер және регрессия функцияларының екеуі де сызықтық болса, онда Х және кездейсоқ шамаларының арасындағы корреляциялық тәуелділік сызықтық корреляция деп аталады.

Корреляцияның таңдама коэффициенті.

Кездейсоқ шамалар арасындағы корреляциялық тәуелділіктің ерекшеліктерін толық сипаттау үшін бұл тәуелділіктің түрін анықтау және ол сызықтық тәуелділік болған жағдайда оның күшін регрессия коэффициентінің шамасы бойынша бағалау жеткіліксіз. 3-суретте екі сызықтық корреляциялық тәуелділіктің -тің Х- ке графиктік суреттемесі келтірілген және регрессияның сәйкес түзу сызықтары бейнеленген.

y Одной из важных задач медицинского исследования является изучение связи между фактором, воздействующим на организм, и параметром – откликом на это воздействие, а также моделирование этого параметра в зависимости от действующего фактора. Эта задача решается методами корреляционного и регрессионного анализа.

а) x б) x

3-сурет

Мұндағы және Х шамаларының арасында корреляциялық тәуелділіктің күші бірдей (ол регрессия сызықтарының сәйкес түзулерінің ОХ осіне енкею бұрыштарының теңдігінен шығады). Алайда 3 а) сур. кескінделген корреляциялық тәуелділік үшін бақылау нүктелерінің регрессия сызығына қарасты шашылуы, 3 б) сур. кескінделген корреляциялық тәуелділікке қарағанда аз. Мұндай жағдайда, қарастырылып отырған корреляциялық тәуелділіктер тығыздығымен ерекшеленеді деп айтады, және 3 а) сур. кескінделген корреляциялық тәуелділік 3 б) сур. келтірілген корреляциялық тәуелділікке қарағанда тығызырақ деп саналады.

Мысалы, орта мектеп оқушыларының жас мөлшері ( ) мен олардың мектепте оқып жатқан оқу жылының (Х) арасындағы корреляциялық тәуелділік, сол сияқты жоғары оқу орнындағы студенттерінің жас мөлшерінің оқу жылына тәуелділігіне қарағанда тығыздау болатыны айқын, себебі жоғары оқу орнында бір жылда оқып жатқан студенттердің арасында жас мөлшерлерінде бір сыныпта оқитын оқушыларға қарағанда үлкен алшақтық (шашылу) болатыны байқалады.

Таңдама бақылау нәтижелері бойынша Х және шамаларының арасындағы сызықтық корреляциялық тәуелділіктердің тығыздығын бағалау үшін сызықтық корреляцияның таңдама коэффициенті ұғымы енгізіледі, және ол

(4)

формуласымен анықталады, мұндағы және - Х және шамаларының сәйкес таңдама орта квадраттық ауытқулары және олар

(5)

формулаларымен есептелінеді. Айта кету керек, сызықтық корреляцияның таңдама коэффициенті -ң негізгі мағынасы, ол сәйкес сызықтық корреляцияның бас коэффициентінің эмпирикалық бағасын береді:

---

(6)

формулаларын ескерсек, - тің Х- ке сызықтық регрессиясының таңдама теңдеуі мына түрде болады:

(7)

мұндағы (регрессия коэффициенті)

Сол сияқты Х - тің -ке сызықтық регрессияның теңдеуін жазуға болады:

(8)

Сызықтық корреляцияның таңдама коэффициентінің негізгі қасиеттері

1. Сызықтық корреляциялық тәуелділікпен байланыспаған екі шаманың корреляция коэффициенті нөлге тең.

2. Сызықтық корреляциялық тәуелділікпен байланысқан екі шаманың корреляциялық коэффициенті 1-ге тең, егер тәуелділік тура (өспелі) болса және -1-ге тең, егер тәуелділік кері (кемімелі) болса;

3. Сызықтық корреляциялық тәуелділікпен байланысқан екі шаманың корреляциялық коэффициентінің абсолюттік шамасы 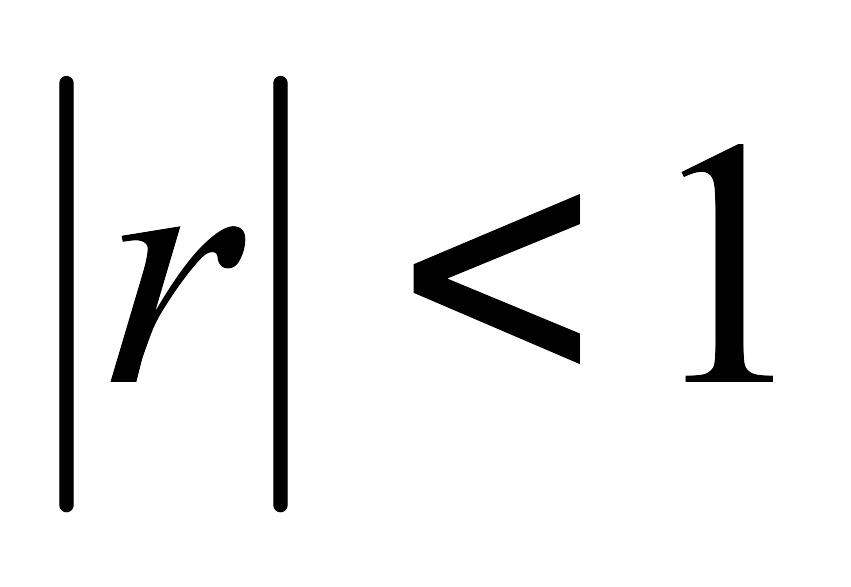теңсіздігін қанағаттандырады. Егер корреляциялық тәуелділік өспелі болса, онда корреляция коэффициенті оң, егер корреляциялық тәуелділік кемімелі болса, онда корреляция коэффициенті теріс.

4. 1-ге неғұрлым жақын болса, 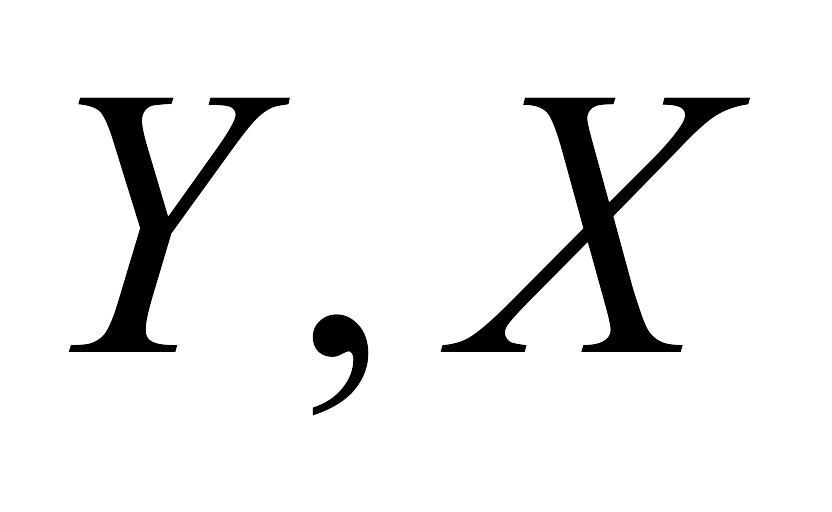шамаларының арасындағы түзу сызықты корреляция соғұрлым тығызырақ.

Корреляциялық байланыс сипатына қарай тура және кері, күшіне қарай күшті, орташа, әлсіз болуы мүмкін.

Параметрлер арасындағы байланыстың күші мен сипаты.

Байланыс күші	Байланыс сипаты
	Тура (+)	Кері (-)
Толық	1	-1
Күшті	0,7 ден 0,999 ге дейін	-0,7 ден -0,999 ге дейін
Орта	0,699 ден 0,3 ге дейін	-0,699 ден -0,3 ге дейін
Әлсіз	0,299 ден 0 ге дейін	-0,299 ден 0 ге дейін
Байланыс жоқ	0	0

Корреляцияның таңдама коэффициентінің

мәнділігі туралы жорамалды тексеру.

Статистикалық өзара байланыс жөнінде сөз болғанда, оның бар болуы немесе жоқ болуы, бағытының болуы (оң немесе теріс) және күшінің сипатымен (күшті, әлсіз) анықталады. Егер зерттеу нәтижесінде нөлдік жорамал теріске шығарылмаса, онда «өзара байланыс жоқ». Нөлдік жорамал теріске шығарылған жағдайда кездейсоқ шамалардың арасында байланыс бар делінеді.

1. Н₀ және Н₁ жорамалдарын тағайындайық:

(яғни, корреляция жоқ),

.

2. мәнділік деңгейін береміз.

3. Критерияның статистикасы:

4. мұндағы - бос дәрежесімен Стьюдент таралуы болатын статистика.

5. болғанда Н₀ жорамалы: мәнділік деңгейімен теріске шығарылады. Демек, параметрлердің арасында мәнді корреляция бар.

болғанда Н₀ жорамалын теріске шығаруға негіз жоқ, яғни параметрлердің арасында мәнді корреляция жоқ.

3 мысал. х және у шамаларының өлшем нәтижелері кестеде берілген.

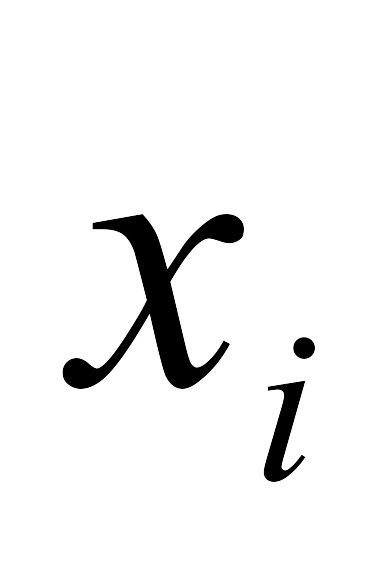
	-2	0	1	2	4
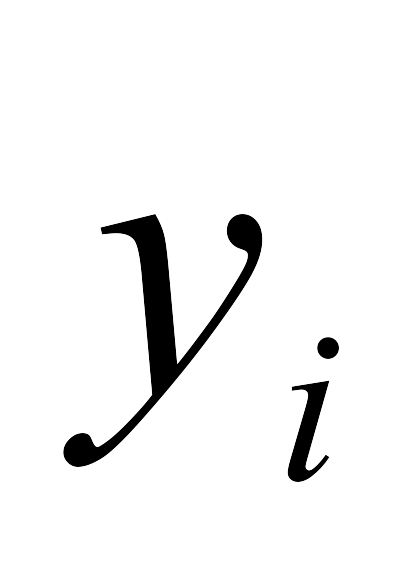
	0,5	1	1,5	2	3

1) y-ң x-қа түзу регрессиясының таңдама теңдеуін;

2) Регрессия сызығын тұрғызу;

3) Корреляцияның таңдама коэффициентін есептеу;

4) Корреляциялық тәуелділіктің сипаты мен күшін анықтау.

Шешуі. Мұнда n=5

1) а) Х пен -тің арасында сызықты тәуелділігі бар деп ұйғарып, ең кіші квадраттар әдісімен және коэффициенттерін табамыз.

---

Смотрите также файлы

• Методические рекомендации для практических занятий.doc

• 4 курс тесты экзамен гастро рус.docx

• 4 курс тесты экзамен кардио рус.doc

• Организации фармацевтической деятельности.doc

• 3_kurs_OFD_kaz.doc