Министерство образования и науки Украины

Приазовский государственный технический университет

Кафедра электроснабжения промышленных предприятий

Троицкая Л.К.
Методические указания

к практическим занятиям
" Электродинамические усилия"
по курсу «Электрические аппараты» для студентов специальности 6.050701 - электротехнические системы электропотребления, дневной, заочной и дистанционной формы обучения


Мариуполь, 2007 г.

Министерство образования и науки Украины

Приазовский государственный технический университет

Кафедра электроснабжения промышленных предприятий
Троицкая Л.К.

Методические указания

к практическим занятиям
" Электродинамические усилия"

по курсу «Электрические аппараты» для студентов специальности 6.050701 - электротехнические системы электропотребления, дневной, заочной и дистанционной формы обучения

Утверждено на заседании

Кафедры "Электроснабжения

промышленных предприятий"

Протокол № 1 от 17.10. 2007


Мариуполь, 2007 г.

УДК 621.313 (076.5)

Методические указания к практическим занятиям «Электродинамические усилия» по курсу «Электрические аппараты» для студентов специальности 6.050701 – электротехнические системы электропотребления дневной, заочной и дистанционной форм обучения /Составили: Л.К. Троицкая – Мариуполь, ПГТУ, 2007 г.
Кафедра электроснабжения промышленных предприятий

Составили: Ст. преподаватель

Троицкая Л. К.
Ответственный за выпуск: Зав. каф. профессор,

докт. техн. наук

Жежеленко И.В.

Рецензент: доцент, к. т. н.

Гаврилов Ф. А.

Утверждено на заседании кафедры «Электроснабжение промышленных предприятий».

Протокол № 1 от " 17 " 10 2007 г.

Содержание

ВВЕДЕНИЕ	5
1. Расчёт электродинамических усилий с использованием закона Био-Савара-Лапласа	6
2. Расчет электродинамических усилий по энергетическим формулам	6
3. Расчет электродинамических усилий при переменном токе	7
4. Примеры решения задач	11
5. Задачи для самостоятельного решения	18
Литература	32
Приложения	34

---

Введение

Решение задач по курсу «Электрические аппараты» требует очень большого объёма дополнительных справочных данных, которые разбросаны по разным справочным изданиям. Кроме этого часто бывают необходимыми для решения каких-либо вопросов расчетные формулы или алгоритмы.

Учитывая, что материалов по курсу «Электрические аппараты» в библиотеке университета недостаточно, издание методических указаний к практическим занятиям, справочных материалов по теоретическим основам электрических аппаратов может оказать действенную помощь студентам дневной, заочной и дистанционной форм обучения по специальности «Электротехнические системы электропотребления» (6.050701), а также студентам других родственных специальностей университета и студентам техникумов.

Справочные данные имеются в двух формах: печатное издание и электронный вариант.

Электродинамические усилия
Электродинамические усилия – это усилия, возникающие в токопроводящих элементах под воздействием с магнитного поля при прохождении по ним электрического тока.
1. Расчёт электродинамических усилий с использованием закона Био-Савара-Лапласа
Электродинамические усилия от действия тока в линейных проводниках можно рассчитать в общем виде по формуле

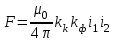; (1.1)

,

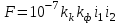где 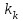- коэффициент контура, который зависит от геометрических размеров проводников и взаимного пространственного расположения, определяется аналитически (см. Приложения 3);

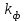- коэффициент формы, который определяется по кривым Двайта, (см. рис. П4), учитывает несимметричность магнитного поля вокруг токопроводящих элементов, где поперечное сечение отлично от круглого, и зависит от формы поперечного сечения, в частности, для проводника круглого сечения 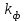=1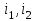

- токи, протекающие по проводникам, А

F- усилие, действующее на проводник, Н
При взаимодействии параллельно расположенных проводников разной длины, силы, действующие на них, одинаковы. Точки приложения равнодействующих сил не находятся в их середине и определяются графоаналитическим путем.

---

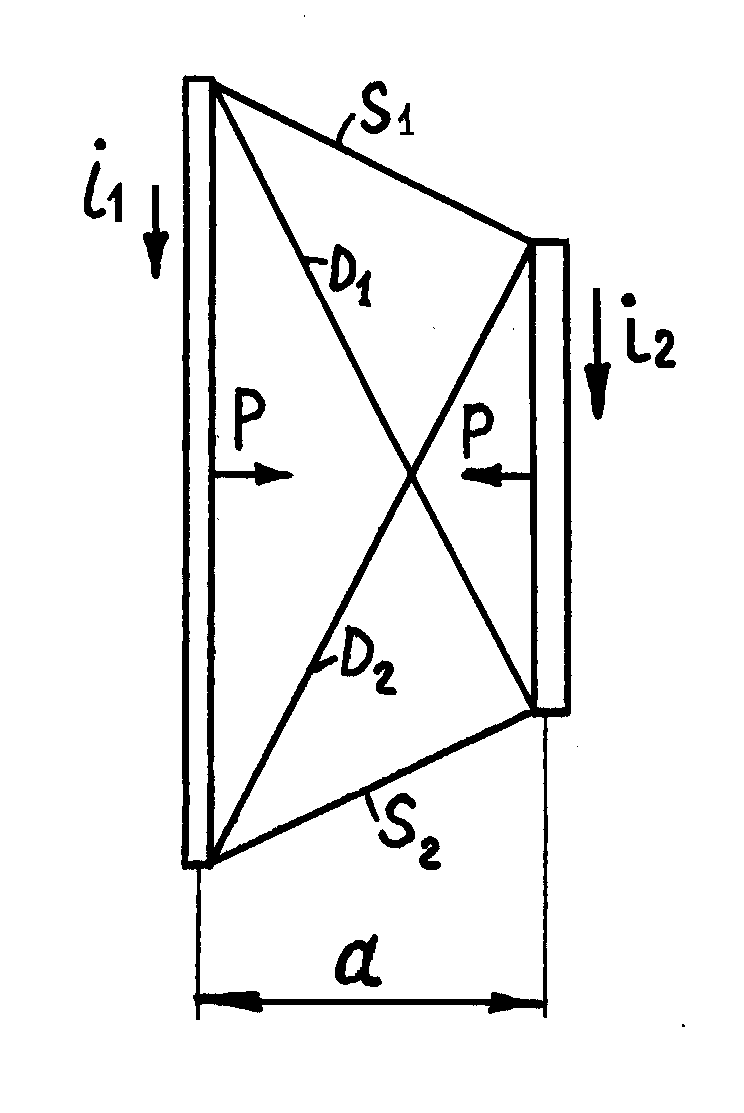
Рисунок 1.1 – Поясняющий рисунок.

2. Расчет электродинамических усилий по энергетическим формулам
Приведенные в этом параграфе зависимости дают возможность освоить метод расчета усилий по энергетическому принципу для наиболее часто встречаю­щихся на практике случаев, т. е. для параллельных шин, полубесконечных петель, катушек, витков, где индуктивность или взаимоиндуктивность контуров может быть выражена как функция координаты, в направлении которой вычисляется сила взаимодействия. При этом использу­ются следующие расчетные формулы и соотношения.

Обобщенное усилие, действующее на проводник при i = const,

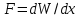, (2.1)

где W — электромагнитная энергия системы, Дж;

x — обобщенная координа­та, м.

В линейных системах, поскольку

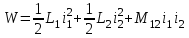; (2.2)

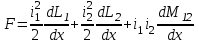, (2.3)

где L — индуктивность системы, Гн.

Электродинамическое усилие в проводниках при изменении поперечного сечения (усилие Двайта)

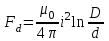, (2.4)

где D, d — соответственно диаметры большего и меньшего поперечного сече­ния, м;

₀ — магнитная проницаемость вакуума, Гн/м

3. Расчет электродинамических усилий при переменном токе
В данном параграфе приведены зависимости для расчета электродинамических усилий, когда по проводникам протекает переменный ток. Так как усилия, действующие на проводники при переменном токе, изменяются во времени, то возникает необходимость в определении и правильном выборе собственной частоты колебаний элементов электрических аппаратов, подвергающихся

---

воздействию этих усилий. Необходимо правильно рассчитать значения мак­симальных усилий, которые зависят от вида и места короткого замыкания в системе. При этом используются следующие расчетные формулы и соотношения.

Электродинамическое усилие между двумя проводниками в однофазной системе

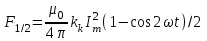, (3.1)

где ₀ = 410^-7— магнитная проницаемость вакуума, Гн/м;

 = 2f — угловая частота тока, с^-1;

I_m — максималь­ное значение тока при синусоидальном законе его изменения, A;

k_k — коэффициент контура электродинамических усилий;

f — частота тока, Гц.

Закон изменения тока при однофазном коротком замыкании

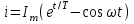, (3.2)

где T—постоянная затухания апериодической составляющей тока, с.

Значение ударного тока короткого замыкания

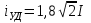, (3.3)

где I — действующее значение установившегося тока короткого замыкания, А.

Значение максимального отталкивающего усилия, действующего на крайние проводники в трехфазной системе при расположении проводников в одной плоскости на одинаковом расстоянии друг от друга:

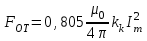. (3.4)

Значение максимального отталкивающего и притягивающего усилий, действующих на средний проводник в трехфазной системе при расположении проводников в одной плоскости на одинаковом расстоянии друг от друга:

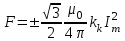. (3.5)

Значение максимального притягивающего усилия, дей­

---

ствующего на крайние проводники в трехфазной системе при расположении проводников в одной плоскости на оди­наковом расстоянии друг от друга,

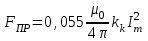; (3.6)

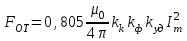. (3.7)

На среднем проводнике 2 (см. рис. 1.1)

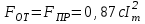. (3.8)

С учётом свободной составляющей тока трёхфазного короткого замыкания.

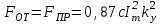. (3.9)
Для двух произвольно расположенных параллельных проводников разной длины (см. рис. 1.1) получена формула

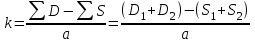, (1.2)

где D – сумма диагоналей трапеции, построенной по размерам взаимодействующих проводников;

S – суммарная длина боковых сторон этой трапеции;

a – расстояние между проводниками.



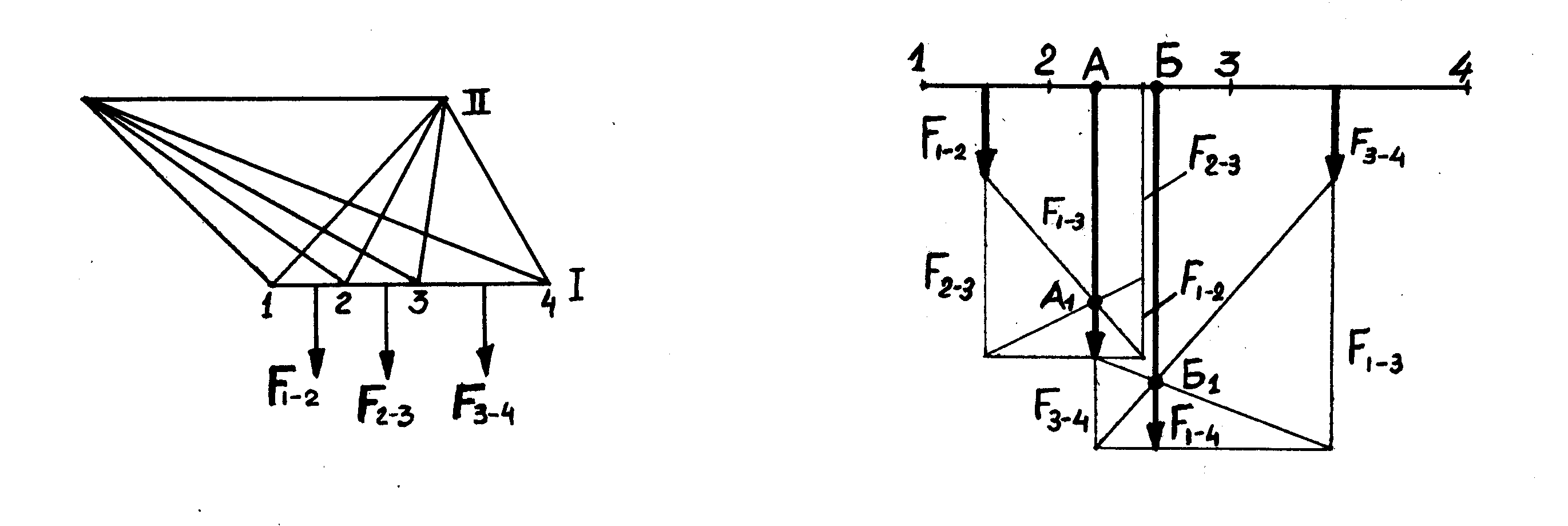
а) б)

Рисунок 1.2 – Определение равнодействующей ЭДУ
При взаимодействии как угодно параллельно расположенных проводников разной длины силы, действующие на них, одинаковы. Точки приложения равнодействующих сил не находятся в их середине и определяются графоаналитическим путем. Рассмотрим определение точки приложения равнодействующей для отрезка I . Отрезок I разбивается на участки (рис. 1.2 а), длина которых тем меньше, чем больше ожидаемое значение индукции на участке. После этого находятся ЭДУ F_1-2 , F_2-3 , F_3-4 , действующие между участками 1-2 , 2-3 , 3 - 4 и проводником II и приложенные посредине этих участков. Для этого вектор F_1-2 продолжаем на длину, равную F_2-3 , а вектор F_2-3 - на длину, равную F_1-2 . На полученных отрезках стоится прямоугольник (рис. 1.2 б). Конец вектора F_1-2 соединяется с нижней правой вершиной, а конец вектора F_2-3 с нижней левой вершиной прямоугольника. Прямая, проведённая параллельно вектору F_1-2 через точку пересечения А₁ является результирующим вектором F_1-3 с точкой приложения А. Аналогично находится равнодействующая векторов F_1-3 и F_3-4 с точкой приложения Б.

---

Смотрите также файлы

• тарих кафедрасы.doc

• 1. Основные положения теории защиты информации.docx

• 2 Расчетная часть 1 Проверочный гидравлический расчёт участка газопровода.docx

• Лекция 1 Матрицы и основные действия над ними. Определители Определение. Матрицей.docx

• 1. Антропометрия занимается изучением .docx