Практическая работа №2

Раздел № 4. Введение в математический анализ

Задача №1

Вариант №3

Дано

Построить графики функций

y = - 4x² + 17x - 4, y  ln( x  2 ), y  sin 2x  1, y =x² - |x|

Решение

Построить график функции общего вида

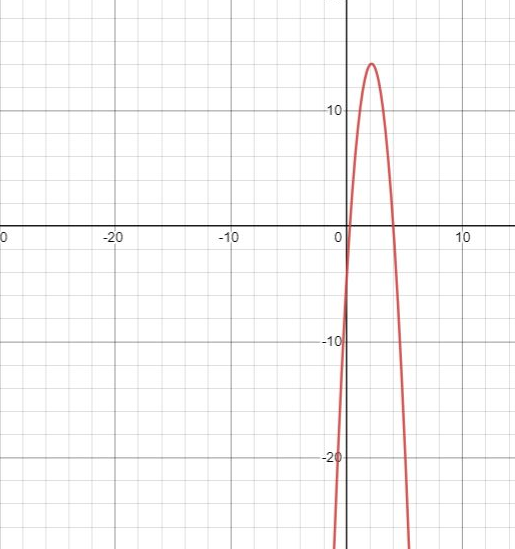
y = - 4 x² + 17x – 4, функция общего вида

x ∈ (− ∞; + ∞)
Для того, чтобы найти экстремумы, нужно решить уравнение:



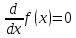
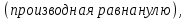
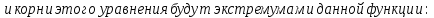
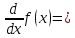первая производная

17−8x = 0


Решаем это уравнение
Корни этого уравнения

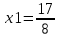Зн. экстремумы в точках:

225

(17/8, ---)

16


Убывает на промежутках

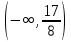Возрастает на промежутках

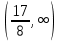Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo

limx→−∞((−4x2+17x)−4) = − ∞

Возьмём предел
значит,
горизонтальной асимптоты слева не существует

limx→∞((−4x2+17x)−4)= − ∞

Возьмём предел
значит,
горизонтальной асимптоты справа не существует

Найдем точки перегибов:

вторая производная

−8=0


Решения не найдены,
возможно перегибов у функции нет

Наклонную асимптоту можно найти, подсчитав предел функции -4*x^2 + 17*x - 4, делённой на x при x->+oo и x ->-oo


Lim

x→−∞ = ∞

---

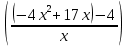Возьмём предел
значит,
наклонной асимптоты слева не существует

Lim

x→−∞ = - ∞
Возьмём предел
значит,
наклонной асимптоты

Проверим чётная или нечётная функция с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:

(−4x2+17x) − 4= − 4x2−17x−4


-Нет

(−4x2+17x) – 4 = 4x2 + 17x + 4


-Нет
значит, функция
не является
ни чётной ни нечётной



y  ln(x  2 )

Строим график y  ln (x)



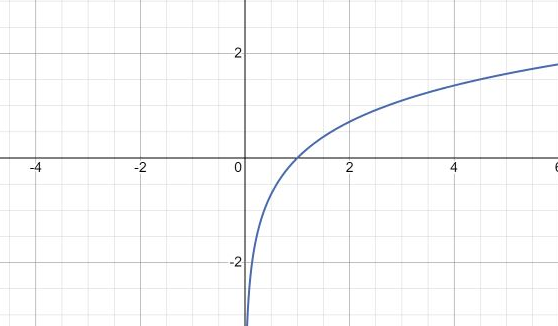
ln (x) = 0 при х=1

ln(x  2 ) = 0 при х = -1, переносим график на 2 деления влево

асимптота х = -2



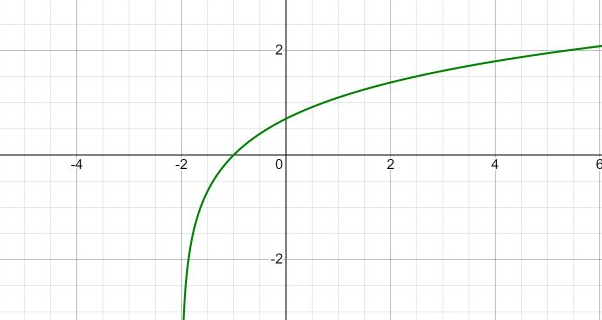
y  sin 2x  1

Строим график y = sin x



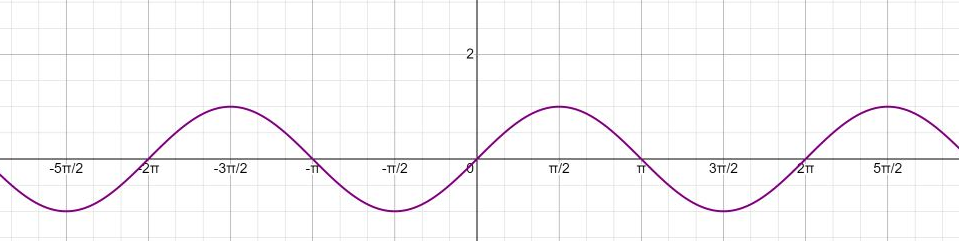
y  sin 2x



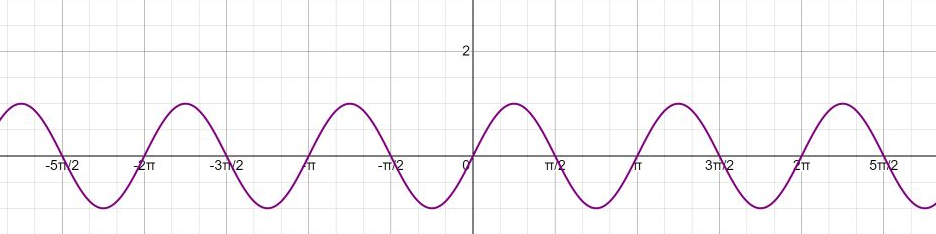
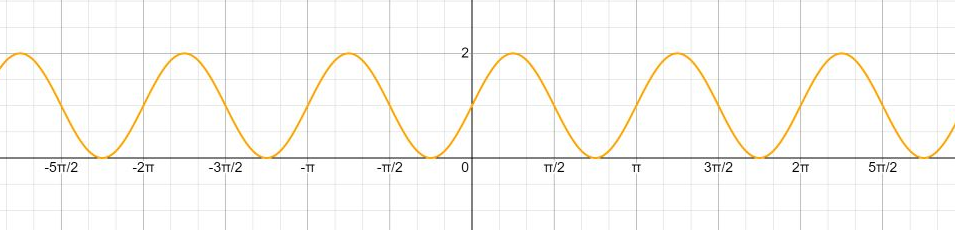
y  sin 2x  1 при sin 2x=1 у =2

при sin 2x=0 у = 1

при sin 2x= -1 у = 0



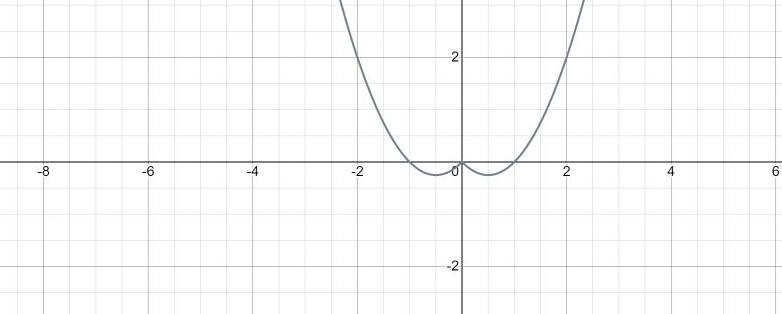
y =x² - |x| график четный

y |х| = y |-х| симметричен



Задание №2

Записать уравнения кривых в полярных координатах и построить их.

Вариант 14

y  0,5, x² + y² = 12, x² +y² = x, x² + y² = - y

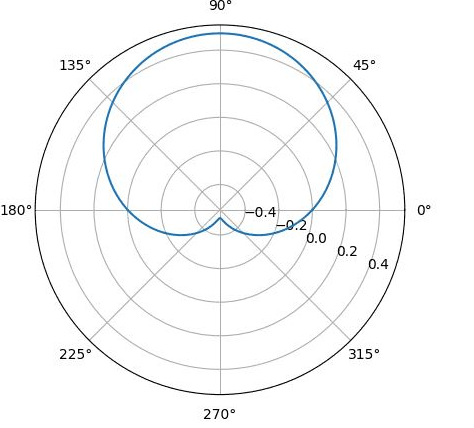
y  0,5

Вводим полярные координаты

y=r·sin φ

x=r·cos φ, получим r·sin φ= ½

r =1/2 sin φ



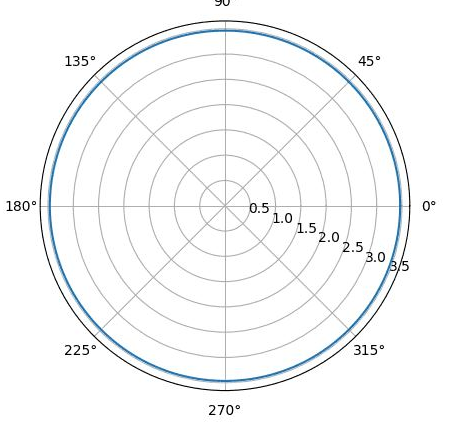
x² + y² = 12,

x=r·cos φ

y=r·sin φ

r²·cos² φ + r²· sin² φ

r²· = 12 r = ±√12 r = √12



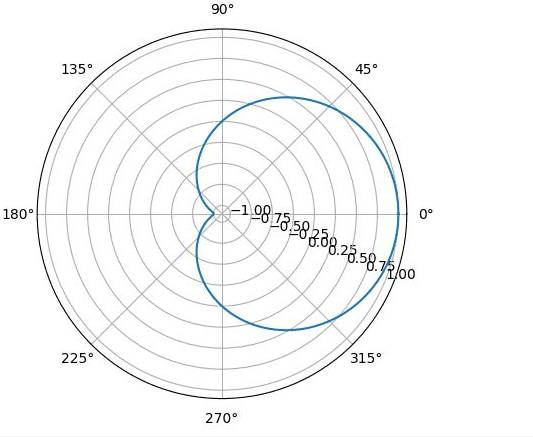
x² +y² = x

r² = r·cos φ

r = cos φ



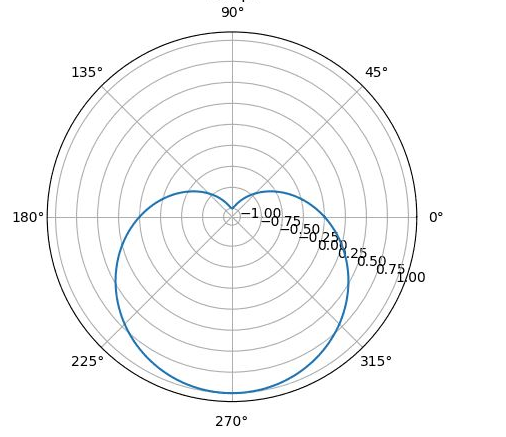
x² + y² = - y

r² = r (-sin φ)

r = - sin φ

---

Задание №3

Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.

Вариант 20

1. 
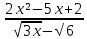   Lim 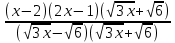= Lim = Lim =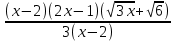
   

x→2 x→2 x→2

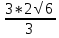= = 2√6

2. 
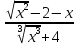   Lim = Lim 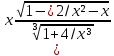= = Lim 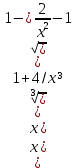= = 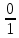0
   

x→∞ x→∞ x→∞
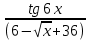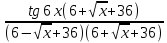3) Lim = Lim = Lim =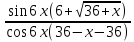

x→0 x→0 x→0

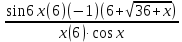= Lim = Lim 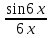∙ 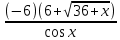= -6 ∙ 12 = -72

x→0 x→0
I замечательный предел Lim 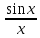= 1

x→0

)

4. 
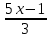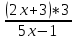
   Lim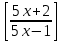 2х+3 = Lim 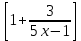2х+3 = Lim 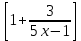= 6/5
   

x→∞ x→∞ x→∞
II замечательный пробел Lim равен е ≈ 2, 718281828459045

x→∞

Lim 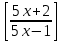2х+3 = е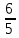

x→∞

4. 
    lim x (lnx – ln(x – 4)) = Lim x ∙ ln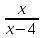 = Lim∙ln 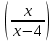² = Lim∙ln 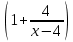² -
   

---

x→∞ x→∞ x→∞ x→∞
= ln∙Lim

---

Смотрите также файлы

• Тема 4 Вскрытие и освоение.pptx

• Анализ результатов опросаанкетирования обучающихся 6 класса мбоу Ясеновская сош.docx

• Методические указания к практическим занятиям по дисциплине Педагогика высшей школы.pdf

• Контрольная работа по биологии для учащихся 5 классов i.doc

• Организационно методические основы реабилитации Определение понятия реабилитация.pptx