Добавлен: 01.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 22
Задача 1.
На вход двухпроводной части стандартного канала ТЧ магистральной сети подается измерительный сигнал с уровнем
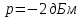. В некоторой точке канала измеренный уровень этого сигнала 
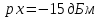. Чему равен относительный уровень в этой точке канала?Для решения задачи применим формулу:
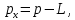
где:
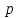- уровень сигнала на входе канала, равный -2 дБм., 
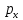- измеренный уровень сигнала в точке канала, равный - 15 дБм., 
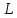- потери на протяжении канала.Подставляя значения в формулу, получим:
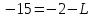
Следовательно, потери на протяжении канала L равны:
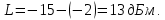
Тогда относительный уровень в этой точке канала равен:
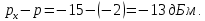
Ответ: Относительный уровень в этой точке канала равен -13 дБ.
Задача 2.
Определить значения несущих частот в первой и второй ступенях преобразования. Исходный сигнал имеет полосу частот 360 − 408 кГц. В первой ступени преобразования сигнал переносится в полосу частот 612 − 660 кГц, используемая боковая − верхняя. Во второй ступени преобразования выделяется нижняя боковая в диапазоне частот 12 − 60 кГц.
Для определения значений несущих частот в первой и второй ступенях преобразования, учитывая заданные полосы частот, следует использовать концепцию смещения несущей частоты и принцип суперпозиции частот.
-
В первой ступени преобразования:
Исходный сигнал имеет полосу частот 360 − 408 кГц. Сигнал переносится в полосу частот 612 − 660 кГц, используя верхнюю боковую. Первая несущая частота в первой ступени будет равна сумме верхней границе полосы частот исходного сигнала и верхней границы полосы частот в первой ступени:
-
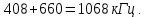
Во второй ступени преобразования:
Выделяется нижняя боковая в диапазоне частот 12 − 60 кГц. Значение несущей частоты во второй ступени будет определяться положением этой нижней боковой частоты. В данном случае, несущая частота во второй ступени будет равна нижней границе диапазона частот нижней боковой модуляции: Несущая частота во второй ступени = 12 кГц.
Таким образом, значения несущих частот в первой и второй ступенях преобразования будут:
-
В первой ступени: 1068 кГц. -
Во второй ступени: 12 кГц.
Задача 3.
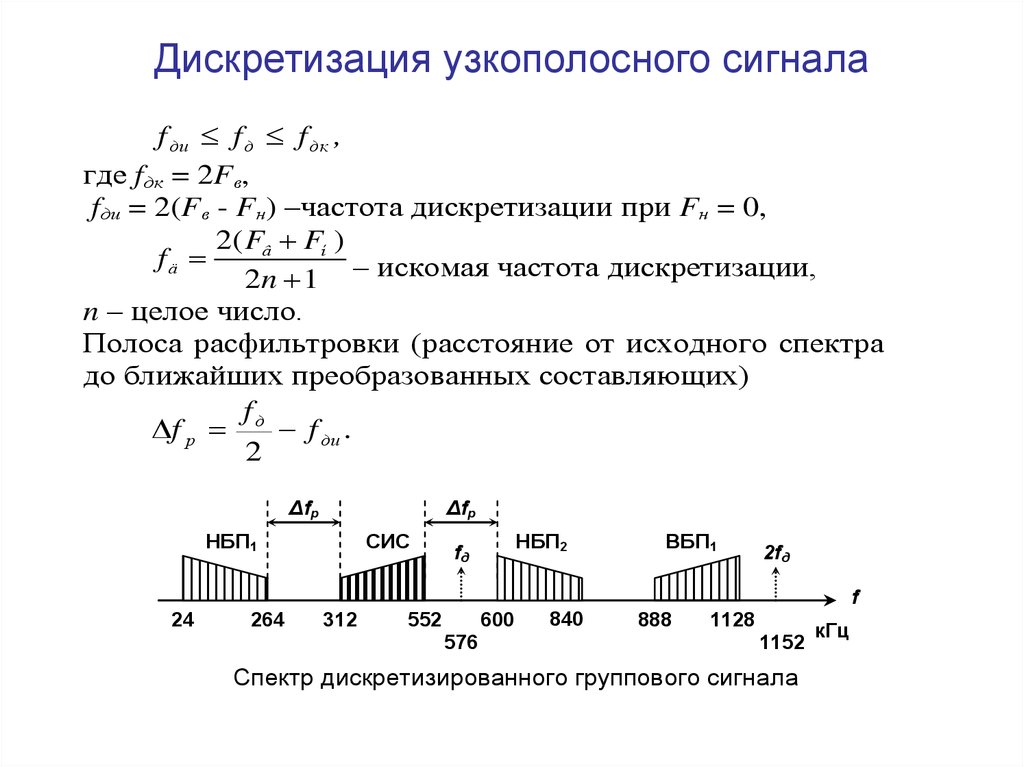
Дискретизации во времени подвергается групповой сигнал, занимающий полосу частот от 250 до 320 кГц. Частота дискретизации равна 240 кГц. Определить максимально допустимую ширину полосы расфильтровки фильтра на выходе канала системы передачи с ВРК, при которой не будет наблюдаться искажений дискретизации.
Исходя из теоремы Котельникова, которая утверждает, что для восстановления сигнала по его дискретным отсчетам необходимо использовать частоту дискретизации как минимум в два раза больше максимальной частоты сигнала. В данном случае максимальная частота группового сигнала составляет 320 кГц, а используется частота дискретизации 240 кГц, что не соответствует условиям теоремы.
Задача 4.
На вход 8 – разрядного кодера системы связи с ИКМ с нелинейной 13 – сегментной шкалой квантования типа А=87,6 и минимальным шагом квантования, равным 8 мВ, поданы импульсы АИМ – 2, амплитудные значения которых равны +356 мВ, -793 мВ. Какова структура кодовых групп, образующихся на его выходе, если в кодере используется цифровой компрессор?
Для сигнала
, 
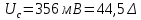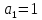, т.к. 
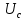положительно.Определение номера сегмента:
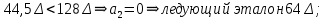
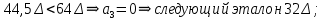
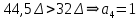
001 – нижняя граница сегмента
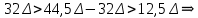4 эталона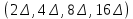 
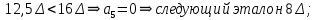
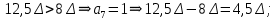
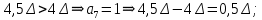
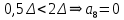
8-разрядная кодовая комбинация на выходе цифрового компрессора – 10010110,
код после экспандирования – P0000001WXYZ1.
Для сигнала
, 
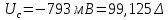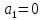, т.к. 
отрицательно.Определение номера сегмента:
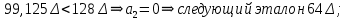
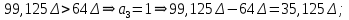
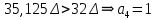
011 – нижняя граница сегмента
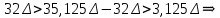4 эталона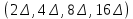 
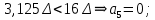
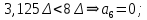
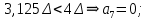
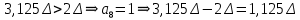
8-разрядная кодовая комбинация на выходе цифрового компрессора – 00110001,
код после экспандирования – P00001WXYZ100.
Матюхин А. Ю. и др. Многоканальные и телекоммуникационные системы. Лабораторный практикум. Ч. 1 - Стр 7 (studfile.net)
