Лабораторная работа №3

«Минимизация логических формул. Получение СДНФ и СКНФ логической формулы с помощью аналитических преобразований»

Цель работы: изучение основных законов и равносильностей алгебры логики, приобретение практических навыков получения МКНФ, МДНФ, СКНФ, СДНФ логических формул.

Ход выполнения лабораторной работы:

1. Получить МКНФ для первой формулы и МДНФ для второй формулы в соответствии с вариантом (уточнить у преподавателя):

№ варианта	Формулы F
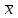	F(x,y)=(( y)(x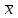y))(( y)( x v y)) F(А,B,C)=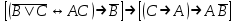
	F(x,y,z)= 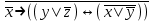F(А,B,C)=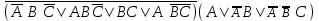
	F(x,y,z)= 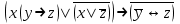F(А,B,C)=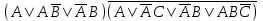
	F(x,y,z)= 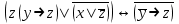F(А,B,C,D)=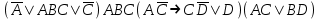
	F(А,B,C,D)= 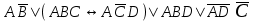F(x,y,z)=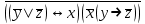
	F(x1, x2, x3)= 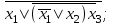F(x,y,z)=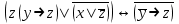
	F(А,B,D)= 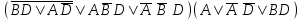F(x,y,z)=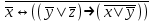
	F(А,B,C,D)= 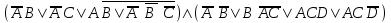F(x,y,z)=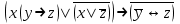
	F(А,B,C)= 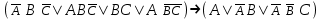F(x1, x2, x3)=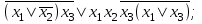
	F(x,y,z)= 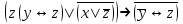F(А,B,C,D)=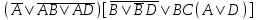
	F(x1, x2, x3) = 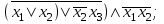F(А,B,C,D) =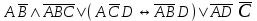
	F(x,y,z)= 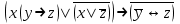(А,B,C,D)=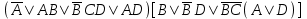
	F(А,B,C)= 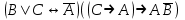F(x1, x2, x3)=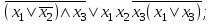
	F(x,y,z)= 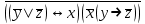F(А,B,C,D)=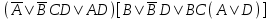
	F(x,y,z)= 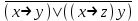F(А,B,C)=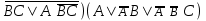
	F(x,y,z)= 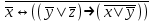F(А,B,C)=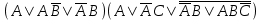
	F(x,y,z)= 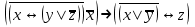F(А,B,C,D)=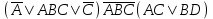
	F(x,y,z)= 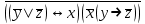F(А,B,C)=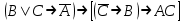
	F(А,B,D)= 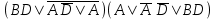F(А,B,C)=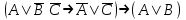
	F(А,B,C)= 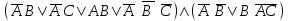F(x,y,z)=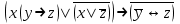
	F(А,B,C)= 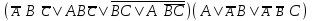F(x,y,z)=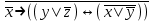
	F(А,B,C)= 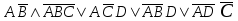F(x,y,z)=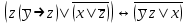
	F(А,B,C,D)= 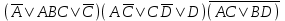F(А,B,C)=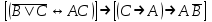
	F(А,B,C)= 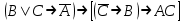F(x, y, z)=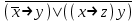
	F(x,y,z)= 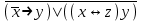F(А,B,C)=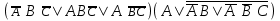
	F(x,y,z)= 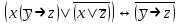F(А,B,C)=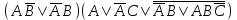
	F(А,B,C)= 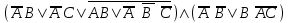F(А,B,C)=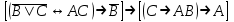
	F(А,B,C)= 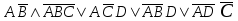F(x,y,z)=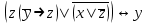

---

2. По каждой из упрощенных формул АНАЛИТИЧЕСКИ (С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЙ) получить их СКНФ и СДНФ соответственно (для первой формулы получить только СКНФ, для второй формулы получить только СДНФ).

3. В пакете схемотехнического моделирования «Electronics Workbench» построить таблицы истинности по исходным формулам (табл.).

а) в EWB получить по ТИ МДНФ для второй формулы; сверить ее с полученной в п.1 формулой;

б) сравнить ТИ исходных формул с полученными СДНФ И СКНФ.

---

Смотрите также файлы

• Тема 10. Цикличность экономической динамики.pdf

• Промежуточная аттестация по обж в 9 классе.doc

• Практическая работа 1 По дисциплине Проектирование информационных систем планирование разработки ис. Диаграммы ганта.docx

• 7модуль тапсырмалары.docx

• Методические рекомендации по воспитанию танцевальной культуры у младшего школьника в детском хореографическом коллективе Выводы по ii главе.rtf