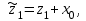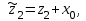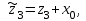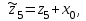ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цифровые логические устройства
Цель работы. Изучить теорию работы цифровых логических устройств и получить навыки их применения в среде программирования LabView.
Дешифраторы
Полный двоичный дешифратор, или декодер (decoder), – это операционный узел ЭВМ комбинационного типа, преобразующий n-разрядный двоичный позиционный код
 в m-разрядный унитарный код, где
в m-разрядный унитарный код, где 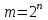 . Унитарный код двоичного n-разрядного числа представляется
. Унитарный код двоичного n-разрядного числа представляется 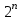 разрядами, только один из разрядов которого равен 1 при нулях на остальных разрядах на любом наборе входных переменных.
разрядами, только один из разрядов которого равен 1 при нулях на остальных разрядах на любом наборе входных переменных. Т
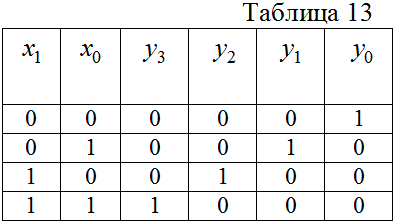
аблица истинности двухразрядного (
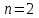 ) дешифратора, имеющего два входа
) дешифратора, имеющего два входа 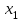 и
и 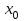 и четыре выхода
и четыре выхода 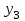 ,
, 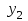 ,
, 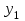 ,
, 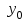 , приведена в табл. 13. По таблице 13 записаны функции описывающие работу дешифратора и представлены в виде
, приведена в табл. 13. По таблице 13 записаны функции описывающие работу дешифратора и представлены в виде 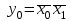 ,
, 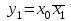 ,
, 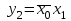 ,
, 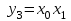 ,
, В
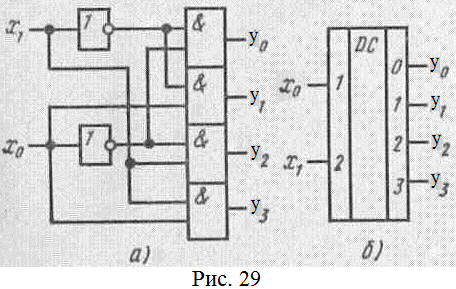
соответствии с системой булевых функций на рис. 29 показаны соответственно функциональная схема дешифратора и его УГО. Инверторы в схеме дешифратора (рис. 29, а) называются адресными формирователями. Они предназначены для того, чтобы каждый вход (
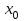 ,
, 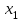 ) представлял собой одну единичную нагрузку. Надпись
) представлял собой одну единичную нагрузку. Надпись
DC на УГО означает decoder. Такой двухразрядный дешифратор иногда называют дешифратором 2х4.
Полные дешифраторы применяются в устройствах управления для дешифрации операций или микрокоманд в управляющие сигналы, а в запоминающих устройствах для выбора ячейки памяти при записи или считывании информации и др.
Кроме полных, дешифраторы могут быть и неполными, реализующими
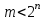 выходов. Такие дешифраторы используются, например, для преобразования двоично-десятичного кода в код, предназначенный для управления десятичным индикатором (дешифраторы 4х10).
выходов. Такие дешифраторы используются, например, для преобразования двоично-десятичного кода в код, предназначенный для управления десятичным индикатором (дешифраторы 4х10). По наличию синхровхода C дешифраторы подразделяются на нестробируемые и стробируемые. Для введения входа стробирования в дешифратор логические элементы И (рис. 29, а) должны содержать три входа. Стробирующий дешифратор при
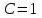 работает в соответствии с таблицей истинности табл. 13, а при
работает в соответствии с таблицей истинности табл. 13, а при 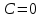 выходные сигналы дешифратора будут равны нулю.
выходные сигналы дешифратора будут равны нулю. Для построения многоразрядных дешифраторов применяют каскадное соединение дешифраторов меньшей разрядности.
Н
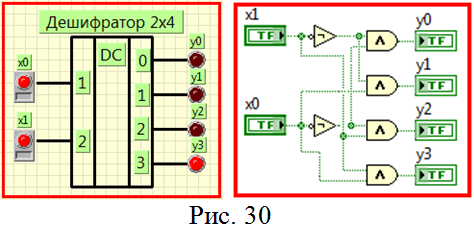
а рис. 30 представлен ВП для исследования принципа действия дешифратора 2х4. Набирая комбинацию входных воздействий с помощью кнопок
 и
и  , исследуем реакцию дешифратора на светодиодных индикаторах
, исследуем реакцию дешифратора на светодиодных индикаторах 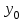 -
- 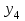 согласно таблице истинности (табл. 13).
согласно таблице истинности (табл. 13). Шифраторы
Шифратор, или кодер (coder), – это операционный узел ЭВМ комбинационного типа, выполняющий функцию, обратную дешифратору, т.е. преобразует унитарный код в двоичный позиционный. Он имеет
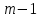 входов и n выходов
входов и n выходов (
 ).
). З
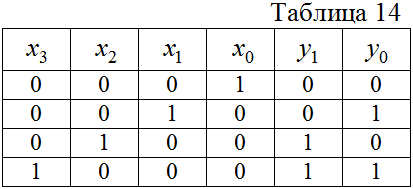
акон функционирования шифратора для
 приведен в табл. 14. При подаче единичного сигнала на один из входов (только на один) на выходе появляется двоичный код номера возбужденного входа.
приведен в табл. 14. При подаче единичного сигнала на один из входов (только на один) на выходе появляется двоичный код номера возбужденного входа. На основании таблицы истинности шифратора (табл. 14) можно записать булевые функции в виде
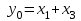
,
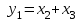
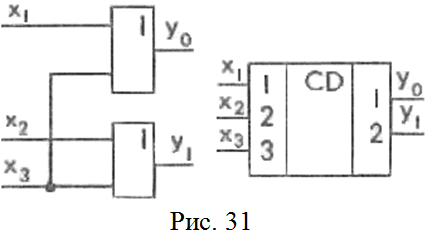
По полученным логическим выражениям разработана функциональная схема шифратора. Функциональная схема шифратора и его УГО показаны на рис. 31. Надпись CD на УГО означает coder.
Д
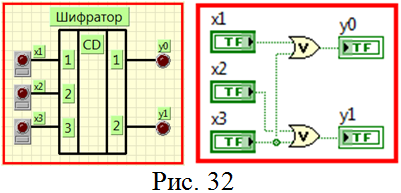 ля исследования принципа действия простейшего шифратора c двумя выходами разработан ВП, представленный на рис. 32. Кнопки
ля исследования принципа действия простейшего шифратора c двумя выходами разработан ВП, представленный на рис. 32. Кнопки  ,
,  и
и  с индикаторами предназначены для формирования входного воздействия, а светодиодные индикаторы –
с индикаторами предназначены для формирования входного воздействия, а светодиодные индикаторы –  и
и  для отображения реакции шифратора на входное воздействие.
для отображения реакции шифратора на входное воздействие. Преобразователи кодов
Преобразователь кода – функциональный узел, преобразующий m-разрядный двоичный код в n-разрядный. Рассмотренные выше дешифраторы и шифраторы представляют собой простейшие преобразователи кодов.
П
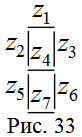
римером преобразователя кодов служит микросхема, преобразующая четырехразрядные двоичные наборы в сигналы управления сегментным десятичным индикатором на светодиодах. Внешний вид семисегментного (выполнен на семи светодиодах
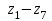 ) десятичного индикатора показан на рис. 33. Такое расположение сегментов индикатора, выполненных на светодиодах, позволяет воспроизводит десятичные цифры от 0 до 9. Например, на индикаторе высвечивается нуль тогда, когда горят светодиоды
) десятичного индикатора показан на рис. 33. Такое расположение сегментов индикатора, выполненных на светодиодах, позволяет воспроизводит десятичные цифры от 0 до 9. Например, на индикаторе высвечивается нуль тогда, когда горят светодиоды 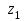
,
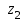 ,
, 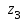 ,
, 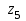 ,
, 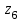 и
и 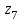 , а единица – когда горят светодиоды
, а единица – когда горят светодиоды 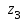 и
и 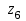 .
. В качестве примера рассмотрим систему отображения информации (СОИ), состоящую из семисегментного десятичного индикатора, четырех светодиодов и десяти кнопочных выключателей без фиксации. При нажатии на одну из кнопок (кроме кнопки с номером нуль) вводится единичная информация на соответствующий вход шифратора системы отображения информации. Шифратор, содержащий 9 входов и 4 выхода, преобразует унитарный код {
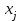 } в двоичный позиционный {
} в двоичный позиционный {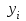 }, согласно табл. 15.
}, согласно табл. 15. 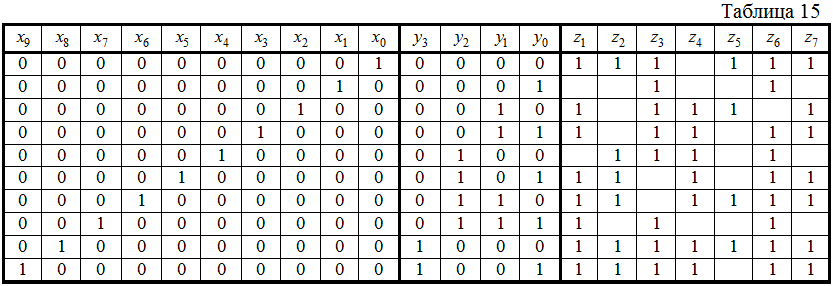
На основании таблицы можно записать логические уравнения, описывающие функционирование шифратора и представить в виде
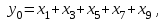
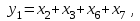
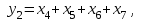
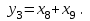
Индикатор из четырех светодиодов
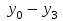 предназначен для отображения двоичных чисел, получаемых на выходе шифратора.
предназначен для отображения двоичных чисел, получаемых на выходе шифратора. Когда не нажата ни одна из девяти кнопок (с номерами 1-9) на выходе шифратора формируется комбинация чисел из нулей. При этом светодиоды семисегментного индикатора не будут гореть, т.е. отображать десятичные числа.
Для отображения нуля на десятичном индикаторе будет использована кнопка с номером 0 и специальная схема формирования и отображения нуля на семисегментном индикаторе.
Для формирования и отображения чисел от 1 до 9 будем синтезировать преобразователь кодов. Двоичному набору
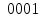
на выходе шифратора соответствует десятичное число единица, т.е.
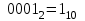 . При этом на десятичном индикаторе должны гореть светодиоды
. При этом на десятичном индикаторе должны гореть светодиоды  и
и  . Это в табл. 15 во второй строчке в столбцах
. Это в табл. 15 во второй строчке в столбцах  и
и  отмечено единицами. Для высвечивания на индикаторе числа 2 должны гореть светодиоды
отмечено единицами. Для высвечивания на индикаторе числа 2 должны гореть светодиоды  ,
,  ,
, 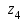 ,
, , и
, и  . Это в третьей строке таблицы в соответствующих столбцах отмечено единицами. Рассуждая аналогично, заполнены все строки таблицы.
. Это в третьей строке таблицы в соответствующих столбцах отмечено единицами. Рассуждая аналогично, заполнены все строки таблицы. Первая строка таблицы будет использована специальной схемой формирования и отображения нуля.
В соответствии с табл. 15 закон функционирования преобразователя кодов представляется в виде
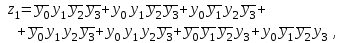
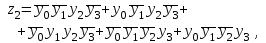
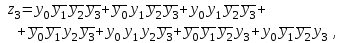
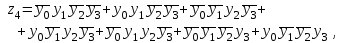
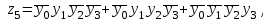
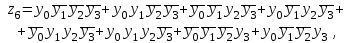
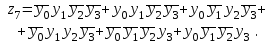
Переключательные функции приведены в совершенной дизъюнктивной нормальной форме (СДНФ) и представляют собой дизъюнкцию (логическая сумма) определенного числа элементарных конъюнкций (логическое умножение). Используя известные методы минимизации переключательных функций, например, метод Квайна, полученные переключательные функции могут быть значительно упрощены.
На основании первой строки табл. 15 формирование нуля кнопкой 0 представляется как: