ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Тема: Определение тангенса и котангенса угла
Составьте конспект, ответив на вопросы:
1. Дайте определение тангенса и котангенса любого угла.
2. Запишите знаки тангенса, котангенса по четвертям.
3. Запишите формулы четности, нечетности тангенса, котангенса.
4. Запишите период тангенса, котангенса
5. Выполните задания:
-
Определите знаки следующих выражений:
а) sin 5̊ ·cos 115̊ ·tg 225̊ ·ctg 235̊
б) cos 68̊ ·sin 246̊ ·tg 135̊ ·ctg235̊
в) tg 35̊ · tg 135̊ ·tg 235̊ ·ctg 72̊
-
Вычислите:
а) 2sin30̊ -tg45̊ +2ctg45̊ +cos90̊
б) 3 – sin2π – 2cos
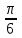 + 3tg
+ 3tg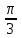 - 4ctg
- 4ctg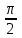
в) ctg 3660̊ г) tg
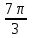 д) ctg
д) ctg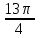
е) tg(-45̊ ) ж) сtg(-240̊ )
з) tg
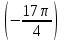 л) tg
л) tg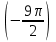
Литература: Лисичкин В.Т. Математика в задачах с решениями: учебное пособие, Лань 2020., Стр.32-38
Режим доступа: https://e.lanbook.com/reader/book/126952
Срок выполнения – до 20 ноября 2020г.
Выполненные задания присылать на электронную почту:
2021.ivanova@mail.ru
Тема письма: Воробьев А., ОЖЭС-112, 16 ноября
Определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Тангенс угла (tg αtg α) - отношение противолежащего катета к прилежащему.
Котангенс угла (ctg αctg α) - отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
П
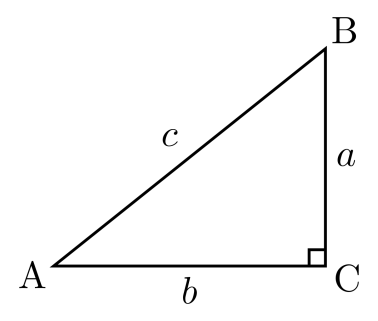 риведем иллюстрацию.
риведем иллюстрацию. В треугольнике ABC с прямым углом С тангенс угла А равен отношению катета BC к катету AС.
В треугольнике ABC с прямым углом котангенс угла А равен отношению катета АC к катету ВС.
Определения тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений тангенса и котангенса - вся числовая прямая, то есть эти функции могут принимать любые значения.
О
 пределения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от −∞ до +∞.
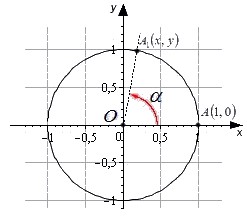
пределения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов. Угол поворота в градусах или радианах выражается любым действительным числом от −∞ до +∞. Можно дать определение тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x, y).
Тангенс угла поворота α - это отношение ординаты точки A1(x, y) к ее абсциссе.
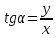
Котангенс угла поворота α - это отношение абсциссы точки A1 (x, y) к ее ординате.
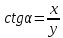
Синус и косинус определены для любого угла поворота, т.к. абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, −1). В таких случаях выражение для тангенса
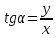 просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.Важно помнить!
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°⋅k, k∈Z
Котангенс определен для всех углов, кроме α=180°⋅k, k∈Z (α=π⋅k, k∈Z)
При решении практических примеров не говорят "синус угла поворота α". Слова "угол поворота" просто опускают, подразумевая, из контекста и так понятно, о чем идет речь.
Знаки тангенса и котангенса по четвертям
Рассмотрим единичную окружность и определи знаки тангенса и котангенса по четвертям
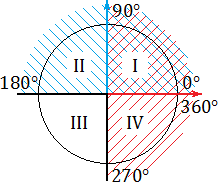 Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс).
Синим цветом обозначено положительное направление оси OY (ось ординат), красным — положительное направление оси OX (ось абсцисс). tg α > 0, если угол α лежит в I или III координатной четверти. Это следует из определения: ведь tg α = y : x , поэтому он положителен лишь там, где знаки x и y совпадают. Это происходит в I координатной четверти (здесь x > 0, y > 0) и III координатной четверти ( x < 0, y < 0).
Во II и IV координатных четвертях тангенс угла отрицательный (т.к. знаки х и у не совпадают)
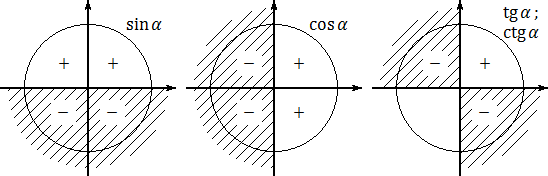
Для наглядности отметим знаки тригонометрической функции —тангенса — в координатной плоскости. Знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.
Получим следующую картинку:
| Периодичность функций tg φ и ctg φ | |||
| Мы знаем, что тангенс угла φ равен ординате соответствующей точки В на оси тангенсов . При повороте вектора ОА, образующего с осью абсцисс угол φ, на 180° против часовой стрелки вектор изменит свое направление на противоположное, но соответствующая точка В на оси тангенсов останется прежней. Поэтому не изменится и тангенс угла. | 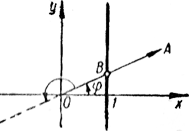 | ||
| Следовательно, при любом φ tg (φ + 180°) = tg φ. Это означает, что функция tg φ является периодической с периодом 180°. Аналогично, для котангенса любого угла φ сtg (φ + 180°) = сtg φ. | |||
| Четность тригонометрических функций. Углы φ и —φ образуются при повороте луча в двух взаимно противоположных направлениях (по часовой стрелке и против часовой стрелки). | 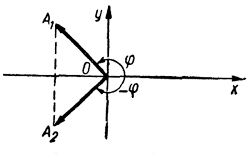 | | |
| Поэтому конечные стороны OA1 и ОА2 этих углов симметричны относительно оси абсцисс. Координаты векторов единичной длины OA1 = (х1 , у1) и ОА2 = (х2, y2) удовлетворяют соотношениям: х2 = х1y2 = —у1 Поэтому cos(—φ) = cosφ, sin (— φ) = —sin φ, Следовательно, синус является нечетной, а косинус — четной функцией угла. | | ||
| Далее имеем: | | ||
| Поэтому тангенс и котангенс являются нечетными функциями угла. | | ||
Значение тангенса, котангенса некоторых углов
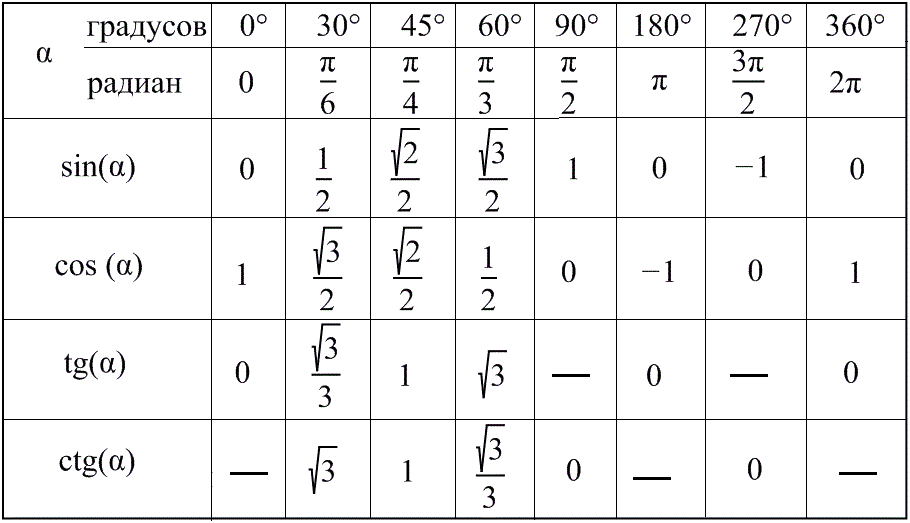
Рассмотрим примеры:
Вычислите:
а) tg 30º +ctg 45º - ctg 60º - 3cos60º =
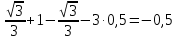
б) tg 225 º = tg(180º + 45º) = tg45º =1 (по свойству периодичности)
в) ctg570º = ctg(180º·3 +30º) = ctg30º =
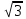
г) tg (-330 º) =- tg330 º = -tg(180 º+ 150 º) = -tg150º = -tg(180º +(-30º)) =-tg(-30º) = - (-
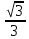 ) =
) = 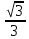
По образцу выполнить задание № 5.