$$$47

Шредингердің стационарлық теңдеуі:

A) Энергияның жуық шамаларына шешімі бар.

B) Кез энергия шамаларына шешімі бар.

C) Қортып шығарылған теңдеу.

D) .

E) .

F) .

G) Сутегі спектріне сәйкес нәтиже береді.

H) Сутегі спектріне қарама - қайшы нәтиже береді.
$$$48

Кванттық механикада физикалық шамаларды оператормен сипаттайды. Анықтама бойынша оператор:

A) Функцияларды сипаттайды.

B) Энергия мәндерін анықтайды.

C) Спинді анықтайды.

D) Дербес функцияларды өзара байланыстырады.

E) Белгілі бір математикалық ереже.

F) Белгілі бір заңдылықтар жиынтығы.

G) Еркін, еріксіз, гармоникалық деп бөлінеді.

H) Сызықты, коммутациялаушы және антикоммутациялаушы деп бөлінеді.
$$$49

Егер кез келген u функциясы үшін , , болса, онда келесі математикалық операциялар нәтижесі ретінде болады:

A) .

B) .

C) .

D) .

E) .

F) .

G) .

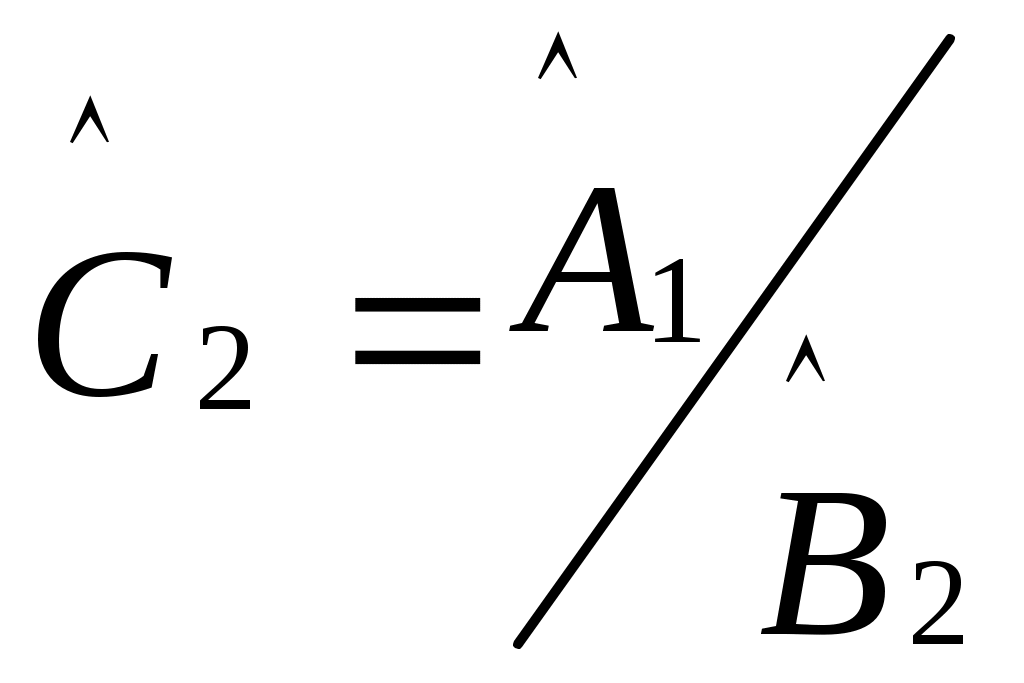H) .
$$$50

Физикалық шамаларды сипаттайтын (кванттық механикада) операторлардын келесі түрлерін бөледі:

A) Қисық сызықты.

B) Гармоникалық.

C) Сызықты емес.

D) Сызықты.

E) Бозондар.

F) Эрмитов.

G) Коммутирленетін және коммутирленбейтін.

H) Фермиондар.
$$$51

Бір қатар операторлар үсынылады А)

---

, Б) , В) , Г) , Д) . Осыдан, және – коммутирленбейтін эрмитов операторлары деп есептесек, онда келтірілген қатарда келесі операторлар эрмитов болады:

A) А.

B) Б.

C) В.

D) Г.

E) Е.

F) А, Б.

G) А, В.

H) А,Г.
$$$52

Сызықтық гармоникалық осциллятордың сипаттамасы бойынша:

A) Осциллятор энергиясы . ............

B) Кездейсоқ тербелістегі бөлшек.

C) Энергия деңгейлерінін арасы бірдей емес.

D) Энергия деңгейлерінін арасы бірдей.

E) Нөлдік энергиясы

F) Нөлдік энергиясы .

G) Нөлдік энергиясы .

H) Нөлдік энергиясы .
$$$53

Бір өлшемді тік бұрышты потенциалдық шұнқырдағы бөлшектін:

A) Жалпы энергиясы нөлге тең.

B) Кинетикалық энергиясы болмайды.

C) Жалпы энергиясы .

D) Деңгейлерінін энергиясы .

E) Деңгейлерінін энергиясы .

F) Энергиясы кез келген мәндер қабылдайды.

G) Энергиясы дискретті мәндер қабылдайды.

H) Энергиясы нөлден артық мәндер қабылдайды.

---

$$$54

Іріктеу ережесіне сәйкес гармоникалық осциллятор қабылдайтын мәндер:

A) .

B) .

C) .

D) .

E) .

F) .

G) .

H) .
$$$55

, , түрінде операторлар жиынтығы берілген болсын, онда кез келген u функциясы үшін олардың түрі:

A) .

B) .

C) .

D) .

E) .

F) .

G) .

H) .
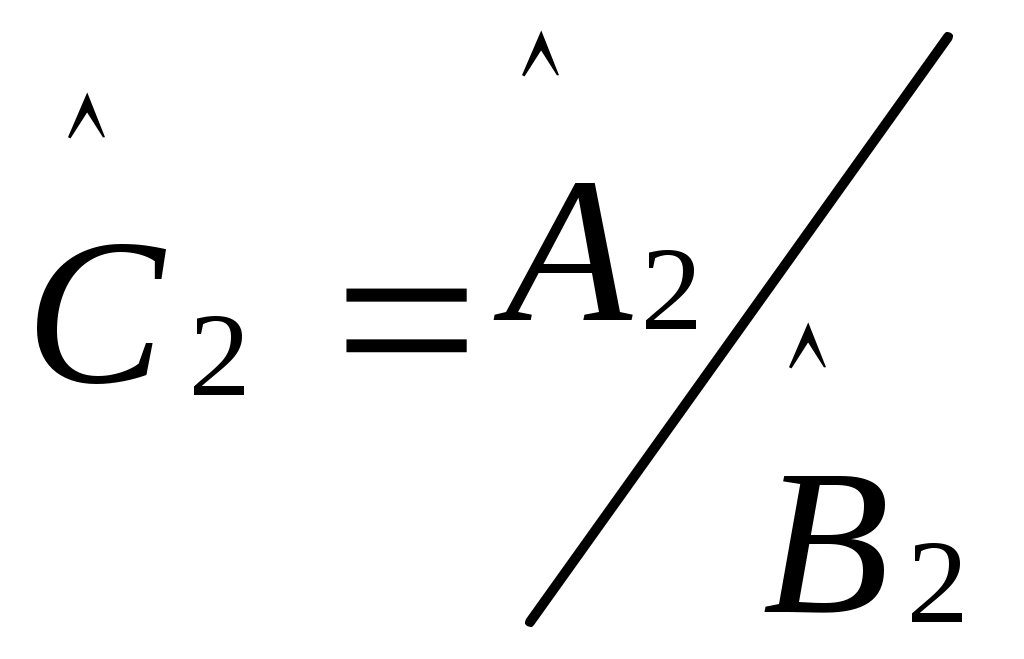$$$56

Ені бір өлшемді тік бұрышты потенциалдық шұнқырдағы электронның үш энергия деңгейін есептеңіз:

A) 4,18 эВ.

B) 11,65 эВ.

C) 37,60 эВ.

D) 8,32 эВ.

E) 33,54 эВ.

F) 55,12 эВ.

G) 22,16 эВ.

H) 51,52 эВ.
$$$57

Ені потенциалдық шұнқырдағы массасы 1 г бөлшектің энергия деңгейлерін есептеңіз. n қандай болғанда осы бөлшектің кинетикалық энергиясы 1 Дж болады?

---

және 16>

---

мәндері арасындағы интервал неге тең (Дж)?:

A) 1,16*10^-20 n² Дж.

B) 0,26*10¹².

C) 0,46*10^-10 Дж.

D) 2,48*10^-16.

E) 2,02*10 Дж.

F) 5,49*10^-61 n² Дж.

G) 1,35*10³⁰.

H) 1,48*10^-30 Дж.
$$$58

Сызықтық гармоникалық осциллятор үшін Шредингер теңдеуінін түрін, энергетикалық деңгейлердің эквидистанттылығын және іріктеу ережесін анықтау керек:

A) .

B) .

C) .

D) .

E) .

F) .

G) .

H) .
$$$59

Толқындық функцияға қойылатын математикалық талаптар бойынша ол:

A) Әртүрлі мәндер қабылдау керек.

B) Кез келген мәнді қабылдау керек.

C) Көп мәнді болу керек.

D) Үзіліссіз болу керек.

E) Дискретті болу керек.

F) Шектелген болу керек.

G) Шектелмеген болу керек.

H) Шексіз болу керек.
$$$60

Электрондар саны Паули принципі (ережесі) бойынша дұрыс көрсетілген деп есептеледі, егер:

A) n=1,l=0 күйде – екі электрон.

B) n=1,l=0 күйде – төрт электрон.

C) n=1,l=1 күйде – екі электрон.

D) n=2,l=1 күйде – екі электрон.

E) n=2,l=0 күйде – екі электрон.

F) n=3,l=1 күйде – алты электрон.

G) n=3,l=0 күйде – алты электрон.

H) n=3,l=2 күйде – алты электрон.
$$$61

Элементар бөлшектер жүйесін сипаттауға кез келген толқындық функция жарамайды, себебі толқындық функция келесі талапқа сәйкес болуы керек:

A) Симметриялы емес анықталған қасиеттерге ие болу.

B) Сызықты.

C) Сызықты емес.

D) Симметриялы.

E) Бір мезгілде симметриялы да, антисимметриялы да.

F) Симметриялық қасиеттерінің мәнісі жоқ.

---

Смотрите также файлы

• Руководство 100 000 руб через 50 дней Как зарабатывать на онлайн фитнесе от уже.pdf

• Отчет о прохождении производственной практики обучающегося Морзовой Алины Витальевны.docx

• Не забывайте, что 1 (1 десятая) это тоже самоечто 10 (десять сотых), даже если вы уверены.pdf

• Времена года.docx

• Реферат по истории мировой литературы человек абсурда в эссе а. Камю миф о сизифе.docx