Файл: Министерство образования республики беларусь белорусский государственный университет.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФАКУЛЬТЕТ РАДИОФИЗИКИ И КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ

Метод стохастического вложения соседей с t-распределениемРефератБыков Георгий АлексеевичСтудент 3 курса, 6 группыcпециальность «компьютерная безопасность»Минск, 2023СодержаниеВведение.................................................................................................3Базовый алгоритм SNE….......................................................................4Проблема скученности и ее решение...................................................5Метод t-SNE..........................................................................................7Вывод.....................................................................................................8Применение...........................................................................................9Программная реализация метода на Python.......................................10Литература: .........................................................................................13

1. 
   Введение
   

Автоматическое уменьшение размерности является важной операцией в машинном обучении как для предварительной обработки данных для других алгоритмов (например, для уменьшения размера входов классификатора), так и в качестве цели самого по себе для визуализации, интерполяции, сжатия и т.д. Существует множество способов "встраивания" объектов, описываемых высокоразмерными векторами или попарными несходствами, в пространство меньшей размерности. Методы многомерного шкалирования [1] сохраняют несходства между элементами, измеряемые либо евклидовым расстоянием, некоторым нелинейным сжатием расстояний, либо кратчайшими путями в графе, как в случае Isomap [2, 3]. Анализ главных компонент (PCA) находит линейную проекцию исходных данных, которая захватывает максимально возможное количество дисперсии. Другие методы пытаются сохранить локальную геометрию (например, LLE [4]) или связать точки высокой размерности с фиксированной сеткой точек в пространстве низкой размерности (например, самоорганизующиеся карты [5] или их вероятностное расширение GTM [6]). Однако все эти методы требуют, чтобы каждый объект высокой размерности был связан только с одним местоположением в пространстве низкой размерности. Это затрудняет раскрытие "многие-к-одному" отображений, в которых один неоднозначный объект действительно принадлежит нескольким отдельным местоположениям в пространстве низкой размерности. В этой статье мы определяем новое понятие встраивания на основе вероятных соседей. Наш алгоритм, стохастическое вложение соседей (SNE), пытается разместить объекты в пространстве низкой размерности таким образом, чтобы оптимально сохранять идентичность соседства и может быть естественно расширен для разрешения нескольких различных изображений с низкими размерностями для каждого объекта.

---

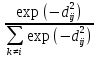
2. Базовый алгоритм SNEДля каждого объекта i и каждого потенциального соседа j мы начинаем с вычисления асимметричной вероятности p_ij того, что i выберет j в качестве своего соседа:p_ij=(1)Расстояния d_ij² могут быть заданы в качестве части определения проблемы (и не обязательно симметричны), или они могут быть вычислены с использованием масштабированного квадрата евклидова расстояния ("сходства") между двумя точками высокой размерности, x_i и x_j:d_ij²= (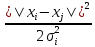2) где σ_i устанавливается вручную или (как в некоторых наших экспериментах) находится методом бинарного поиска значения σ_i, которое делает энтропию распределения соседей равной log k. Здесь k - это эффективное количество локальных соседей или "непонятность", и выбирается вручную.В пространстве низкой размерности мы также используем гауссовские окрестности, но с фиксированной дисперсией (которую мы без потерь общности устанавливаем равной 1/2), так что индуцированная вероятность q_ij того, что точка i выберет точку j в качестве своего соседа, является функцией низкоразмерных изображений y_i всех объектов и задается выражением:q_ij=(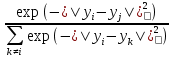3)Цель вложения заключается в наилучшее соответствие между этими двумя распределениями. 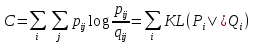Это достигается путем минимизации функции стоимости, которая является суммой расхождений Кульбака-Лейблера между исходными (pij) и вызванными (qij) распределениями по соседям для каждого объекта: (4)Размерность пространства y выбирается вручную (гораздо меньше, чем число объектов).Заметим, что увеличение q_ij, когда p_ij маленький, приводит к потере некоторой вероятности в распределении q, поэтому есть стоимость за моделирование большого расстояния в пространстве высокой размерности с помощью маленького расстояния в пространстве низкой размерности, хотя это менее затратно, чем моделирование маленького расстояния с помощью большого. В этом отношении SNE улучшает методы, такие как LLE [4] или SOM [5], в которых широко разнесенные точки данных могут быть "схлопнуты" в качестве ближайших соседей в пространстве низкой размерности. Интуиция состоит в том, что SNE подчеркивает локальные расстояния, а его функция стоимости четко обеспечивает как сохранение изображений близких объектов рядом, так и сохранение изображений широко разнесенных объектов относительно далеко друг от друга.

---

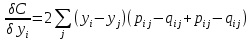
Дифференцирование C трудоемко, потому что y_k влияет на q_ij через нормализующий термин в уравнении 3, но результат простой:(5)Это имеет приятную интерпретацию в виде суммы сил, тянущих yi к yj или отталкивающих его от нее в зависимости от того, наблюдается ли j как сосед чаще или реже, чем ожидалось. Учитывая градиент, существует множество возможных способов минимизации C, и мы только начали поиск лучшего метода. Метод наискорейшего спуска, в котором все точки регулируются параллельно, неэффективен и может застрять в плохих локальных оптимумах. Добавление случайного дрожания, уменьшающегося со временем, находит гораздо лучшие локальные оптимумы и является методом, который мы использовали для примеров в этой статье, хотя он все еще довольно медленный. Мы инициализируем вложение, помещая все низкоразмерные изображения в случайные местоположения, очень близко к началу координат. В разделах 5 и 6 обсуждаются несколько других методов минимизации, включая отжиг перплексии.

3. 
   Проблема скученности и ее решение
   

Хотя SNE создает достаточно хорошие визуализации, он затрудняется функцией стоимости, которую сложно оптимизировать, и проблемой, которую мы называем «проблемой скученности». Здесь я покажу другой способ, называемый «t-SNE» (t-Distributed Stochastic Neighbor Embedding), который облегчит эти проблемы. Функция стоимости, используемая t-SNE, отличается от используемой SNE двумя способами: (1) она использует симметричную версию функции стоимости SNE с более простыми градиентами, которую кратко представили Кук и др. и (2) она использует распределение Стьюдента вместо гауссовского для вычисления сходства между двумя точками в пространстве с низкой размерностью. t-SNE использует t распределение в пространстве с низкой размерностью, чтобы облегчить как проблему скученности, так и проблемы оптимизации SNE. Рассмотрим набор данных, состоящий из точек, лежащих на двумерном изогнутом многообразии, которое приблизительно линейно на малой шкале и вложено в пространство более высокой размерности. Возможно, что малые попарные расстояния между точками можно моделировать довольно хорошо в двумерной карте, что часто иллюстрируется на примерах, таких как набор данных «Swiss roll». Теперь предположим, что многообразие имеет десять скрытых измерений и вложено в пространство гораздо более высокой размерности.

---

Существует несколько причин, по которым попарные расстояния в двумерной карте не могут точно моделировать расстояния между точками на десятимерном многообразии. Например, в десяти измерениях возможно иметь 11 точек данных, которые взаимно находятся на одинаковом расстоянии, и нет способа точно моделировать это на двумерной карте. Связанная проблема - это очень разное распределение попарных расстояний в двух пространствах. Объем сферы, центрированной на точке данных i, масштабируется как r^m, где r - радиус, а m - размерность сферы. Поэтому, если точки данных примерно равномерно распределены в области вокруг i на десятимерном многообразии, и мы пытаемся моделировать расстояния от i до других точек данных на двумерной карте, возникает проблема "скученности": площадь двумерной карты, доступная для размещения среднего удаленных точек данных, будет далеко не такой большой по сравнению с площадью, доступной для размещения близких точек данных. Поэтому, если мы хотим точно моделировать малые расстояния на карте, большинство точек данных будут скучены в узких областях, и неудачная их расстановка на карте приведет к тому, что многообразие будет деформировано.Проблема скученности возникает при попытке визуализации данных с высокой размерностью в двухмерной карте. Для каждой точки данных i нужно соединять пружиной слишком далекие от нее точки на карте, что приводит к очень слабым притягивающим силам. Несмотря на то, что эти силы очень малы, большое количество таких сил приводит к сжатию точек в центре карты, что предотвращает образование промежутков между естественными кластерами. Следует отметить, что проблема скученности не специфична только для SNE, но также возникает в других локальных методах многомерного масштабирования, таких как картирование Сэммона.

3. 
   Метод t-SNE
   

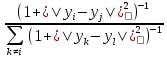
В методе t-SNE мы используем стьюдентовское t-распределение с одной степенью свободы (которое является эквивалентом распределения Коши) в качестве тяжелохвостого распределения в низкоразмерном отображении. Используя это распределение, совместные вероятности qi j определяются какq_ij=(6)Мы используем распределение стьюдентовского t-распределения с одной степенью свободы, потому что

---

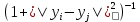
оно обладает особенно хорошим свойством, что приближается к обратному квадратному закону для больших попарных расстояний 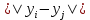в низкоразмерной карте. Это делает отображение совместных вероятностей на карте (почти) инвариантным к изменениям масштаба карты для точек, находящихся далеко друг от друга. Это также означает, что большие кластеры точек, находящиеся далеко друг от друга, взаимодействуют так же, как отдельные точки, поэтому оптимизация происходит одинаково на всех, кроме самых мелких, масштабах. Теоретическое обоснование использования t-SNE основывается на ряде математических теорем.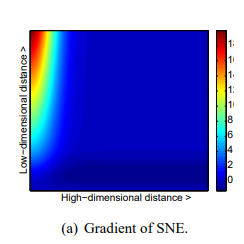



Algorithm : Simple version of t-Distributed Stochastic Neighbor Embedding.

Data: data set X = {x₁, x₂,..., x_n},

cost function parameters: perplexity Perp,

optimization parameters: number of iterations T, learning rate η, momentum α(t). Result: low-dimensional data representation Y (T) = {y₁, y₂,..., y_n}.

begin

compute pairwise affinities p_ij with perplexity Perp (using Equation 1)

set p_ij =

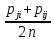
sample initial solution Y (0) = {y₁, y₂,..., y_n} from N (0,10−4 I)

for t=1 to T do

compute low-dimensional affinities qi j (using Equation 4)

compute gradient δC δY (using Equation 5)

set Y (t) = Y (t−1) +η δC δY +α(t) Y (t−1) −Y (t−2)

end

end

3. 
   Вывод
   

Выбор распределения Стьюдента t обусловлен тем, что оно тесно связано с нормальным распределением, так как распределение Стьюдента t является бесконечной смесью нормальных распределений. 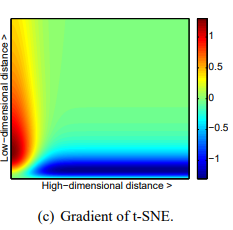Удобство вычислений заключается в том, что вычисление плотности точки в распределении Стьюдента t гораздо быстрее, чем в нормальном распределении, потому что оно не включает экспоненту, хотя распределение Стьюдента t эквивалентно бесконечной смеси нормальных распределений с различными дисперсиями.Во-первых, градиент t-SNE сильно отталкивает несхожие данные, которые моделируются малым попарным расстоянием в низкоразмерном представлении. SNE также имеет такое отталкивание, но его эффект минимален по сравнению с сильными притяжениями в других частях градиента (наибольшее притяжение в нашем графическом представлении градиента составляет примерно 19, тогда как наибольшее отталкивание составляет примерно 1). В UNI-SNE количество отталкивания между несхожими данными немного больше, однако это отталкивание сильно только тогда, когда попарное расстояние между точками в низкоразмерном представлении уже большое (что часто не является случаем, поскольку низкоразмерное представление инициализируется выборкой из гауссовского распределения с очень маленькой дисперсией, центрированного вокруг начала координат).

---