Файл: Отчет по лабораторной работе 3 Выбор процедурного и объектноориентрованного языков программирования для решения квадратного уравнения.docx
Добавлен: 02.12.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации Федерально государственное автономное образовательное учреждение высшего образования «Южно-Уральский государственный университет»
Факультет «Архитектурно-строительный институт»
Кафедра «Водоснабжение и водоотведение»
ОТЧЕТ
По лабораторной работе №3
«Выбор процедурного и объектно-ориентрованного языков программирования для решения квадратного уравнения»
Руководитель работы: ст. преподаватель
______________________/С.В. Сяськов
«____» _____________________ 2020 г.
Автор работы: студент гр. АСЗ-205
__________________/Э.Д. Мирсодиков
«____» _____________________ 2020 г.
Челябинск 2020
Задание
Написать программу для решения квадратного уравнения на процедурном языке программирования и оформить отчет по ней в программе MS Word.
Отчет должен содержать:
- титульный лист
- лист задания
- ГСА
- сравнительный анализ процедурных языков программирования
- выбор языка программирования
- листинг (с комментариями в исходном коде на русском языке)
- экранные формы
- сравнительны анализ объектно-ориентированных языков программирования
- выбор объектно-ориентированного языка программирования на базе их сравнительного анализа
- листинг (с комментариями в исходном коде на русском языке)
- экранные формы
- выводы
- библиографический список
Уравнение вида ax² + bx + c = 0, где а ≠ 0, называют квадратным уравнением.
a – первый коэффициент;
b – второй коэффициент;
c – свободный член уравнения;
a, b, c - действительные числа.
Если, а = 1, то квадратное уравнение называют приведенным.
Если, а ≠ 1, то квадратное уравнение называют неприведенным.
Корни уравнения вида ax² + bx + c = 0 определяют по формуле:
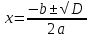
D – дискриминант квадратного уравнения, рассчитывается по формуле:
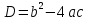
Если D=0, то уравнение имеет один корень.
Если D<0, то уравнение не имеет решения.
Если D>0, то уравнение имеет два корня.
Если b = 0, то квадратное уравнение называется неполным и принимает вид: ax² + c = 0
В этом случае корень уравнения находится по формуле:
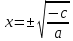
Если с = 0, получим квадратное уравнение без свободного члена вида: ax² + bx = 0, где
корень уравнения равен нулю, х = 0
Графическая схема алгоритма представлена на рисунке 1.
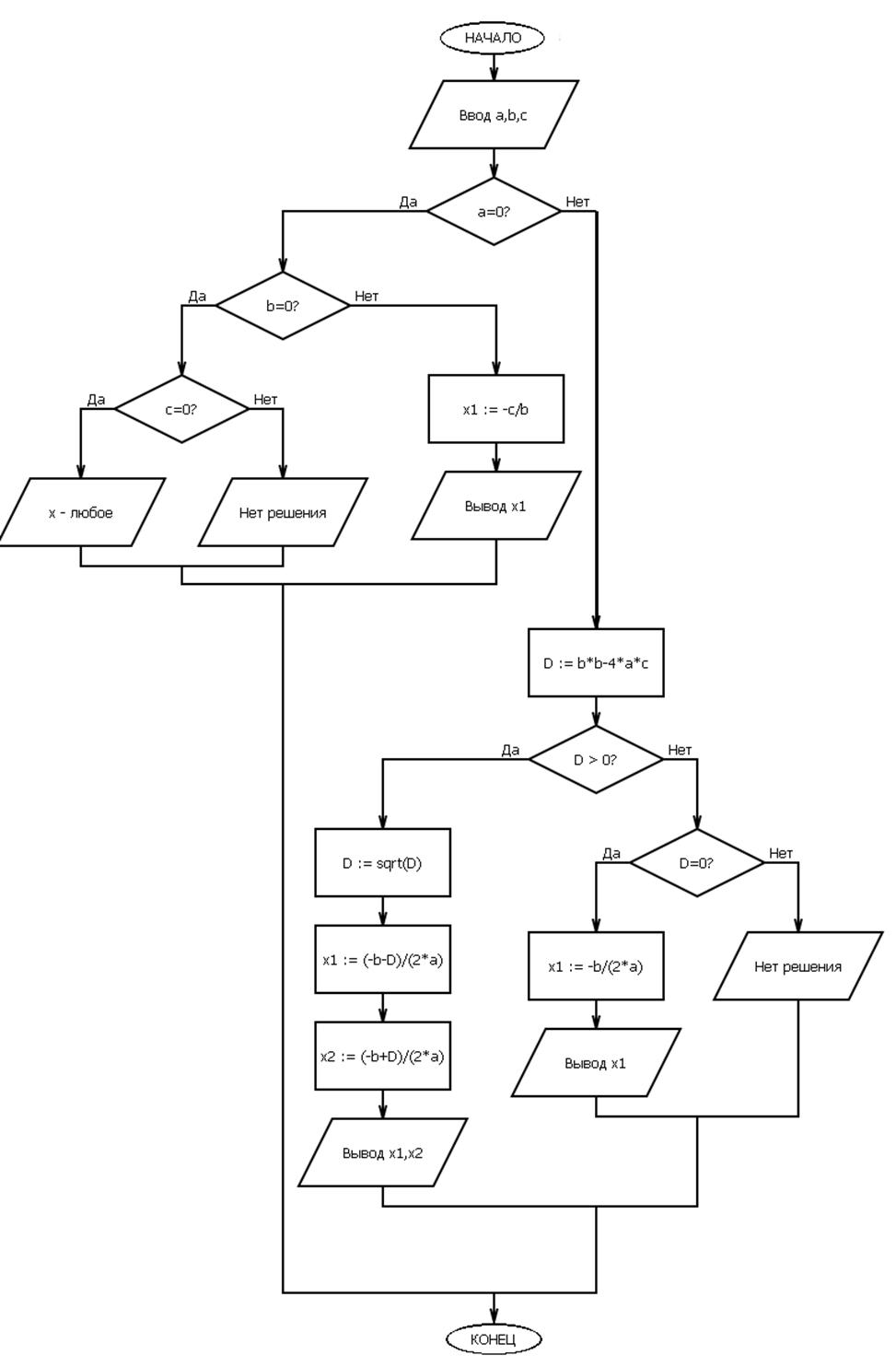
Рисунок 1. Блок-схема
Сравнительный анализ процедурных языков программирования
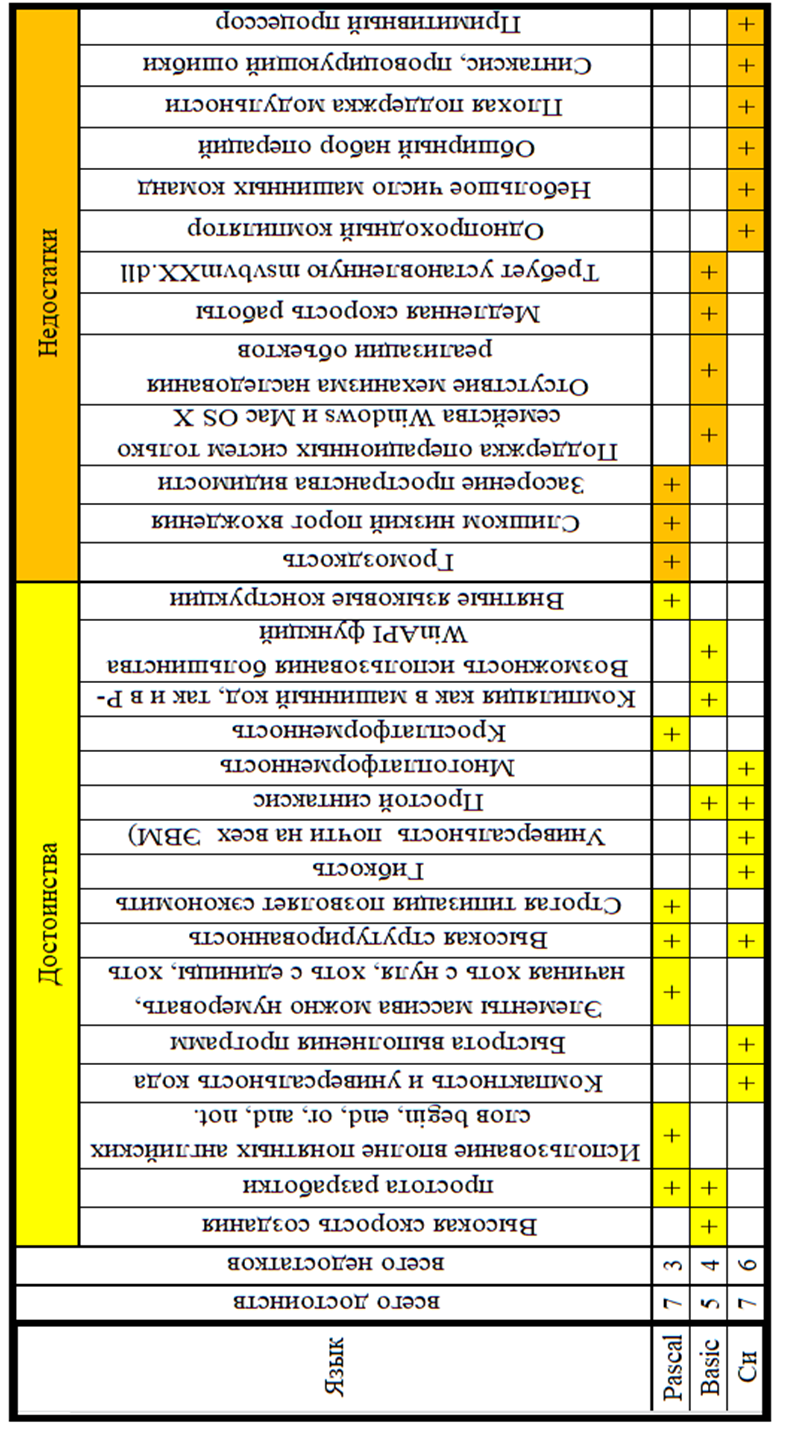
Сравнивая процедурные языки программирования, считаю наиболее оптимальным для решения квадратного уравнения, применения языка Паскаль.
Листинг (с комментариями в исходном коде на русском языке):
Программа на языке Pascal.
Program korni; {Программа называется korni}
Var a, b, c, d: real; {a, b, c – коэффициенты уравнения, d- дискриминант}
x1, x2 : real; {х1, х2 - корни}
begin
writeln (' a');
readln (a);
writeln (' b');
readln (b);
writeln (' c');
readln (c);
if a=0 then writeln {'Для а=0 применение алгоритма невозможно.'}
else begin
d:=b*b-4*a*c;
if d<0 then writeln {Корней нет'};
if d=0 then begin x1:= -b/2/a;
writeln('x=',x1:6:2);
end;
if d>0 then begin
x1:= (-b+sqrt(d))/2/a; x2:= (-b-sqrt(d))/2/a;
writeln ('x1=',x1:6:2, ' x2=',x2:6:2); {‘Корни уравнения:’}
end;
end;
end.
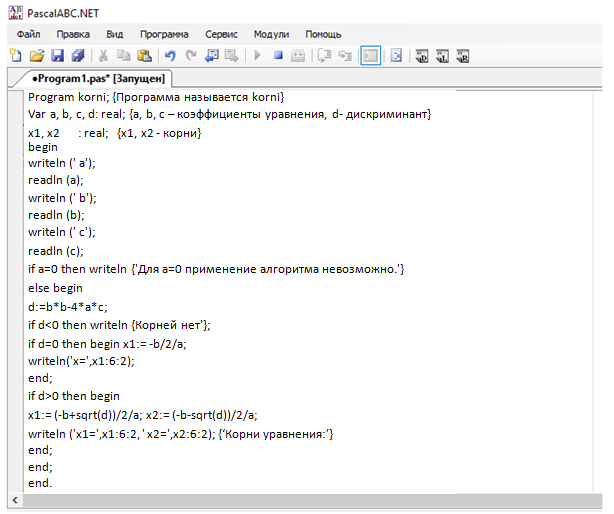
Рисунок 2. Скриншот экрана
Сравнительны анализ объектно-ориентированных языков программирования
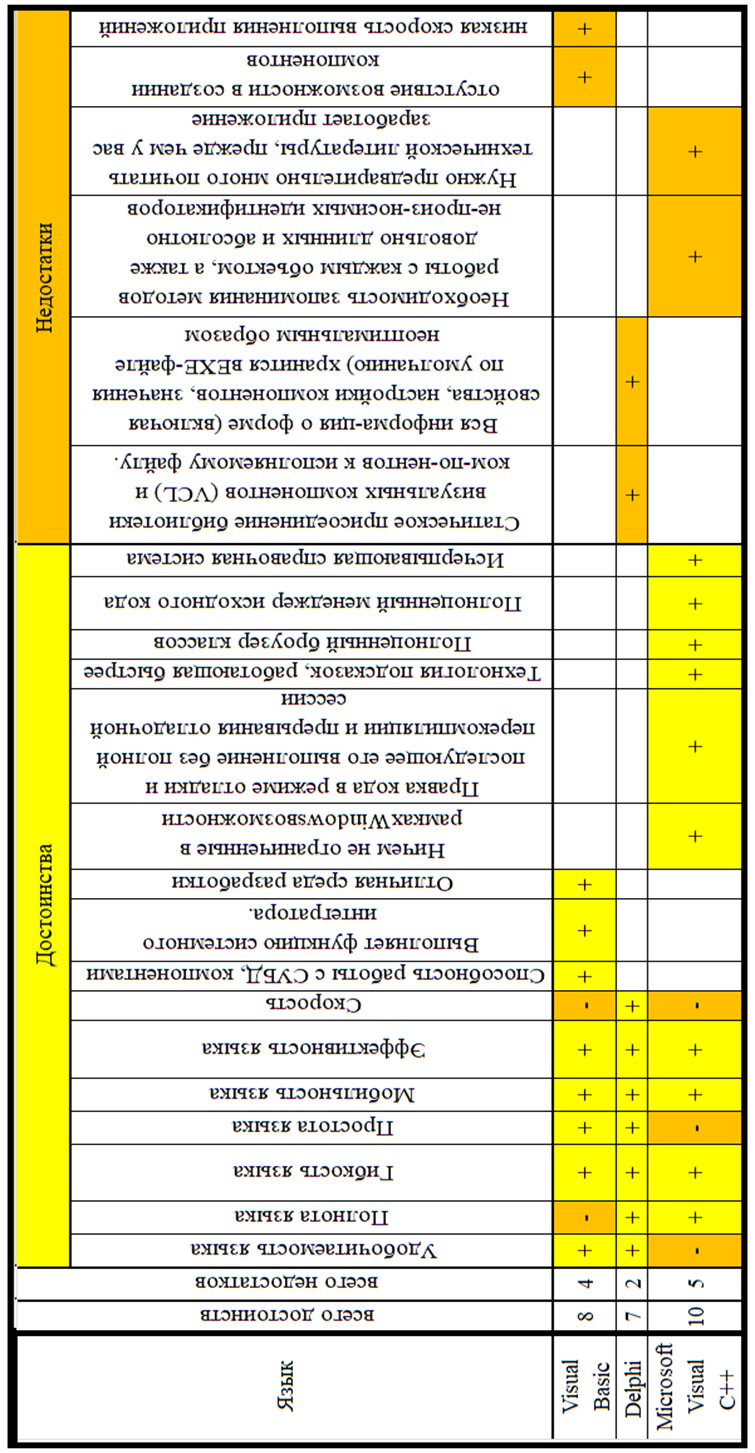
Задача. Составить программу решения квадратного уравнения ax2+bx+c=0.
Учитывая все достоинства и недостатки, считаю наиболее оптимальным применения языка Visual basic
Решение.
Алгоритм.
Запросить значение переменных а, b и c .
Присвоить D значение b2 – 4* a * c .
Если D > 0, то:
Присвоить х1 значение (-b-sqr(D))/2*a
Присвоить х2 значение (-b+sqr(D))/2*a
Сообщить значение х1 и х2
Иначе если D =0, то:
Присвоить х значение (-b)/2*a
Сообщить значение х
Иначе:
Сообщить «Уравнение корней не имеет».
Конец если.
Конец.
Рассмотрим блок-схему решения данной задачи:
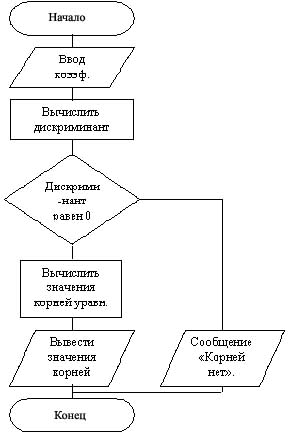
Написаниепрограммногокода
procedure SqRoot(Editi,Edit2,Edit3:tEdit;Label2:tLabel);
var
a,b,c:real; {Коэффициенты уравнения}
d:real; {Дискриминант}
xl,x2:real; {Корни уравнения}
begin
{Ввод исходных данных} a:=StrToFloat(Editl.text);
b:=StrToFloat(Edit2.text);
с:=StrToFloat(Edj.t3.text);
{ Вычисление дискриминанта } d:=Sqr(b)-4*a*c;
if d=0 then begin
Label2.color:=clRed;
Label2.font.color:=clRed;
Label2.caption:='Дискриминант меньше нуля.'+#10+
'Уравнение не имеет корней.' end else
begin
{Вычисление корней}
х1:=(-b+Sqrt(d))/(2*a);
x2:=(-b-Sqrt(d))/(2*а);
{ Вывод результата - значений корней}
Label2.font.color:=clBlack;
Label 2.caption='Корни уравнения:' +#10+'xl=1+FloatToStr(xl)
+#13+'x2='+FloatToStr(x2);
end;
end.
Экранныеформы
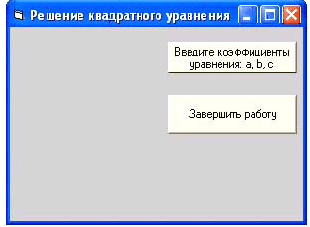
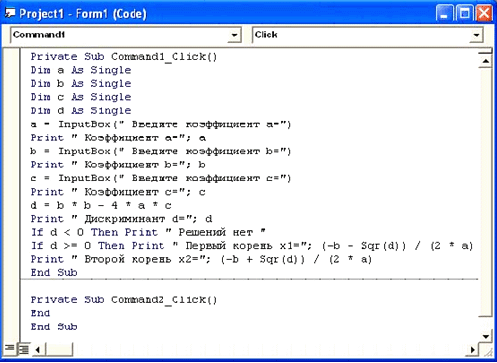
Вывод
Нет самого удобного языка программирования, каждому нужно своё и под определённые нужды. Все они обладают своими положительными и отрицательными качествами, которые будут так или иначе влиять на процесс разработки.
Список использованной литературы
-
Гради Буч «Объектно-ориентированный анализ и проектирование с примерами приложений»
2. Бадд, Т. Объектно-ориентированное программирование в действии / Т. Бадд. - СПб.: Питер, 2011. - 464 с.
3. Буч, Г. Объектно-ориентированный анализ и проектирование с примерами приложений на C++ / Г. Буч; пер. с англ. И. Романовский, Ф. Андреев. - М.: Бином, 2012. - 560 с.
4. Казакова А.Е. Методологические основания развития языков программирования: диссертация по ВАК 09.00.08. - М., 2008. - Режим доступа: dissertCat.com.
5. Дал, У.И. Симула-67: Универсальный язык программирования / У.И. Дал, Б. Мюрхауг, К. Нюгорд; пер. с англ. К.С. Кузьмина, Е.И. Яковлева. - М.: Мир, 2011. - 100 с.
6. https://urok.1sept.ru0>