Файл: Лабораторная работа 1 по дисциплине Вычислительная математика студент группы по 01з.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Федеральное государственное образовательное учреждение высшего образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра программной инженерии
Лабораторная работа №1 по дисциплине
Вычислительная математика
Выполнил: студент группы ПО 01з
Рыков И.Ю.
Проверила: доцент, Кочура Е. П.
Курск 2022
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Получаемое на ЭВМ решение y почти всегда, за редким исключением, содержит погрешность, т.е. является приближенным.
1. Основные источники и классификация погрешностей математического моделирования
а) математическая модель является приближенным описанием реальной научной, инженерной или иной практической задачи;
б) исходные данные содержат погрешности, т.к. они получены в результате измерений или других расчетов;
в) математические методы в большинстве случаев являются приближенными;
г) из-за ограниченности разрядности вычислительной машины и используемых способов представления чисел в ЭВМ при вводе и выводе, а также при выполнении арифметических операций производятся округления, т.е. для представления числа используется меньше разрядов, чем в самом числе. Обычно используются два способа округления: по усечению и дополнению.
Величина погрешности н, соответствующая первым двум причинам называется неустранимой погрешностью. Погрешность м источником которой является вычислительный метод называется погрешностью метода. Погрешность в, возникающая при вводе и выводе чисел, а также при выполнении арифметических операций на ЭВМ, называется вычислительной погрешностью.
Максимальная относительная погрешность округления, возникающая в ЭВМ при вводе и выводе вещественных чисел, а также при выполнении арифметических операций с этими числами называется машинным эпсилон ..
Минимальное по модулю число, представимое в ЭВМ называется машинным нулем. Любое меньшее по модулю число в ЭВМ будет представлено как нуль.
Машинное эпсилон определяется количеством разрядов в ячейке памяти, которое отводится для хранения мантиссы числа, а машинный нуль определяется количеством разрядов, которое отводится для хранения порядка.
2. Абсолютная и относительная погрешность. Количество верных знаков в числе
Пусть a-точное значение некоторой величины, которое может быть и неизвестно, а*-известное приближенное значение этой величины. Положительная величина
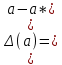называется абсолютной погрешностью величины a. Отношение абсолютной погрешности величины а к ее абсолютному значению называется относительной погрешностью.
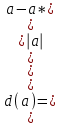(2.1)Максимальное значение (а) называется предельной абсолютной погрешностью и обозначается (а). Соответственно предельная относительная погрешность равна:
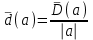. (2.2)Обычно слово “предельное” опускают и под абсолютной и относительной подразумевают абсолютную и относительную предельные погрешности.
На практике, в таблицах часто вместо погрешности указывается количество верных знаков. Количество верных знаков в числе отсчитывается от первой значащей цифры числа до первой значащей цифры абсолютной погрешности.
3. Погрешности арифметических операций:
а) при сложении и вычитании двух величин их абсолютные предельные погрешности складываются:
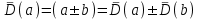. (2.3)б) при умножении и делении двух величин на друга их относительные предельные погрешности складываются:
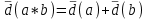, (2.4)
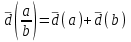. (2.5)в) при возведении в степень приближенной величины ее относительная предельная погрешность умножается на показатель степени:
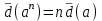. (2.6)4. Погрешность функций
Пусть а-приближенное значение аргумента x функции y=f(x), а а- абсолютная погрешность аргумента, т.е.
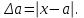
При а<<1 для оценки абсолютной погрешности и относительной погрешностей функции используются следующие определение/
Абсолютной погрешностью функции y называется произведение модуля производной функции на абсолютную погрешность аргумента, а относительной погрешностью функции y называется отношение абсолютной погрешности функции к ее абсолютному значении, т.е.
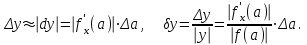(2.7)Аналогичные соотношения можно записать для функции нескольких переменных, например, если U=f(x,y,z), то при:
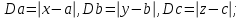
имеет:
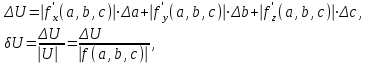(2.8)где
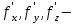частные производные, по соответствующим аргументам.5. Определение машинного нуля и машинного эпсилон.
Для определения машинного нуля необходимо в цикле провести вычисления отношения y=1/xi, xi=10-i, i=1, 2,…. Как только величина xi станет меньше машинного нуля, произойдет деление на нуль. Предыдущее значение xi и будет машинным нулем.
При выполнении операции сложении двух чисел 1+ начиная с некоторого <<1 из-за округления будет получено результирующее число 1. Поскольку точное значение суммы должно быть равно 1+, а получаемое значение равно 1, то для абсолютной погрешности суммы имеем: (1+)=1+-1=. Так как по определению машинное эпсилон есть относительная погрешность округления, то получаем
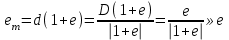.Таким образом, если определить такое наибольшее значение при котором 1+=1, то это значение будем равно ..
С этой целью в цикле достаточно организовать вычисление последовательности: n+1=n/2, n=0,1,..., начиная с 0=1 и проверку выполнения условия 1+n+1=1. Так как при некотором значении n из-за погрешности округления условие 1+n+1=1 будет выполнено
, то имеем =n+1.
ЗАДАНИЕ (вариант 20)
1. Разработать текст программы для вычисления машинного нуля и машинного эпсилон.
2. Провести теоретический вывод формулы для оценки абсолютной и относительной погрешности функции U(x,y,z):
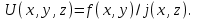
Вид функций f(x,y), (x,z) указан в таблице индивидуальных заданий.
3. Разработать текст программы для вычисления абсолютной и относительной погрешности функции U(x,y,z).
4. На ЭВМ набрать и отладить программу.
5. Провести расчет абсолютной и относительной погрешности функции U(x,y,z), для указанных в таблице значений аргументов, считая, что эти исходные данные имеют относительную погрешность
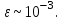Результаты занести в таблицу.6. Для выполнения пункта 5 можно использовать пакеты С++, DELPHY, ТУРБО ПАСКАЛЬ, MATHCAD и др..
using System;
namespace ConsoleApp4
{
class Program
{
private static void Main(string[] args)
{
if (args is null)
{
throw new ArgumentNullException(paramName: nameof(args));
}
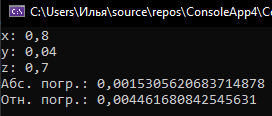
Console.Write(value: "x: ");
float x = float.Parse(s: Console.ReadLine());
Console.Write(value: "y: ");
float y = float.Parse(s: Console.ReadLine());
Console.Write(value: "z: ");
_ = float.Parse(s: Console.ReadLine());
double dU1 =
((Math.Abs(value: 1 / (x * (x - y))) -
(Math.Log10(d: x - y) / Math.Pow(x: x, y: 2))) * (Math.Abs(value: x) * 0.001F)) +
(Math.Abs(value: -(1 / (x * (x - y)))) * (Math.Abs(value: y) * 0.001F));
Console.WriteLine(value:
$"Абс. погр.: {dU1}\n" +
$"Отн. погр.: {dU1 / Math.Abs(value: Math.Log(d: x - y) / x)}");
_ = Console.ReadKey();
}
}
}
| Наименование величины | Численные значения |
| Относительная погрешность функций U | 0,0044 |
| Абсолютная погрешность функций U | 0,0015 |
Ответы на контрольные вопросы:
1. Математическая моделирование – метод исследования объектов и
явлений реального мира с помощью их приближенных описаний на
языке математики.
2. 1) Построение модели
2) Решение математической задачи, к которой приводит модель.
3) Интерпретация полученных следствий из математической модели.
4) Проверка адекватности модели.
5) Модификация модели.
3. а) математическая модель является приближенным описанием реальной
научной, инженерной или иной практической задачи;
б) исходные данные содержат погрешности, т.к. они получены в
результате
измерений или других расчетов;
в) математические методы в большинстве случаев являются
приближенными;
г) из-за ограниченности разрядности вычислительной машины и
используемых способов представления чисел в ЭВМ при вводе и выводе,
а
также при выполнении арифметических операций производятся
округления,
т.е. для представления числа используется меньше разрядов, чем в самом
числе.
4. По виду представления, различают абсолютную, относительную и
приведённую погрешности.
5. Округление — замена числа на его приближённое значение (с
определённой точностью), записанное с меньшим количеством значащих
цифр.
6. Пусть a-точное значение некоторой величины, которое может быть и
неизвестно, а*-известное приближенное значение этой величины.
Положительная величина ∆( a ) = a - a* называется абсолютной
погрешностью величины a. Отношение абсолютной погрешности
величины а
к ее абсолютному значению называется относительной погрешностью.
7. Предельная абсолютная погрешность суммы приближенных чисел равна
сумме предельных абсолютных погрешностей слагаемых, т. е.
Δ u = Δ x + Δ y (1.13)
Из формулы (1.13) следует, что предельная абсолютная погрешность суммы
не может быть меньше предельной абсолютной погрешности наименее
точного из слагаемых, т. е. если в состав суммы входят приближенные
слагаемые с разными абсолютными погрешностями, то сохранять лишние
значащие цифры в более точных не имеет смысла.
8. На практике, в таблицах часто вместо погрешности указывается
количество
верных знаков. Количество верных знаков в числе отсчитывается от первой
значащей цифры числа до первой значащей цифры абсолютной погрешности
9. Машинный нуль — числовое значение с таким отрицательным порядком,
которое воспринимается машиной как ноль. Машинный эпсилон —
числовое значение, меньше которого невозможно задавать относительную
точность для любого алгоритма, возвращающего вещественные числа.