Файл: Самостоятельная работа по геометрии 7 класс Признаки равенства прямоугольных треугольников.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 203

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Самостоятельная работа по геометрии 7 класс «Признаки равенства прямоугольных треугольников»

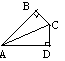1 вариант.

1. Даны два прямоугольных треугольника АВС, АВD (рис 1). Доказать: ∆АВС = ∆АDC.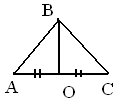

Найти ВАD, если ВС = СD, АСВ = 55°.
Рис 1.

2. Дан ΔАВС, ВО – высота (рис 2).

Доказать: Δ АВО = ΔОВС Рис 2.

Найдите АВ, если А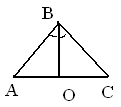= 30° , ВО = 6 см.
3 .Дано ΔАВС – равнобедренный,

ВО – биссектриса ( рис 3).

Доказать: Δ АВО= Δ ОВС

Найдите ВО, если В = 60°, АВ =26 см.

Рис 3.

4. Дан треугольник АВС, где угол В = 90°. Внешний угол при вершине А равен 120°, сторона АВ равна 7 см. Чему равна длина гипотенузы?
5. Один из углов прямоугольного треугольника равен 60 0, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.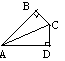
1 вариант.

1. Даны два прямоугольных треугольника АВС, АВD (рис 1). Доказать: ∆АВС = ∆АDC.

Найти ВАD, если ВС = СD, АСВ = 55°.
Рис 1.

2. Дан ΔАВС, ВО – высота (рис 2).

Доказать: Δ АВО = ΔОВС Рис 2.

Найдите АВ, если А= 30° , ВО = 6 см.
3 .Дано ΔАВС – равнобедренный,

ВО – биссектриса ( рис 3).

Доказать: Δ АВО= Δ ОВС

Найдите ВО, если В = 60°, АВ =26 см.

Рис 3.

4. Дан треугольник АВС, где угол В = 90°. Внешний угол при вершине А равен 120°, сторона АВ равна 7 см. Чему равна длина гипотенузы?
5. Один из углов прямоугольного треугольника равен 60 0, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.

Самостоятельная работа по геометрии 7 класс «Признаки равенства прямоугольных треугольников»

2 вариант.

1.Даны два прямоугольных треугольника ∆АВС, ∆АDC

( рис1). АС - биссектриса,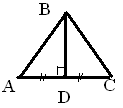

ВАС = 35˚. Доказать: ∆АВС = ∆АDC. Найти ВСD.




Рис 1.

2. Дан ΔАВС, ВD – высота (рис 2)

Доказать: Δ АВD = Δ DВС.

Найдите ВD, если А= 30° , АВ = 16 см. Рис 2.
3. Дан равнобедренный ΔАВС,ВО – биссектриса (рис 3).

Доказать: Δ АВО= Δ ОВС

Н айдите АВ, если А = 60°, АО = 8 см
Рис 3.

4. Дан треугольник АВС, где угол С = 90°. Внешний угол при вершине В равен 150°, сторона АС равна 10 см. Чему равна длина гипотенузы?
5. Один из углов прямоугольного треугольника равен 30 0, а сумма гипотенузы и меньшего катета равна 48 см. Найдите гипотенузу
2 вариант.

1.Даны два прямоугольных треугольника ∆АВС, ∆АDC

( рис1). АС - биссектриса,

ВАС = 35˚. Доказать: ∆АВС = ∆АDC. Найти ВСD.




Рис 1.

2. Дан ΔАВС, ВD – высота (рис 2)

Доказать: Δ АВD = Δ DВС.

Найдите ВD, если А= 30° , АВ = 16 см. Рис 2.
3. Дан равнобедренный ΔАВС,ВО – биссектриса (рис 3).

Доказать: Δ АВО= Δ ОВС

Н айдите АВ, если А = 60°, АО = 8 см
Рис 3.

4. Дан треугольник АВС, где угол С = 90°. Внешний угол при вершине В равен 150°, сторона АС равна 10 см. Чему равна длина гипотенузы?
5. Один из углов прямоугольного треугольника равен 30 0, а сумма гипотенузы и меньшего катета равна 48 см. Найдите гипотенузу

Смотрите также файлы