ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение:
1) ΔАВС - прямоугольный:
АС = ВС = 4 см.2) ΔНВС- прямоугольный:
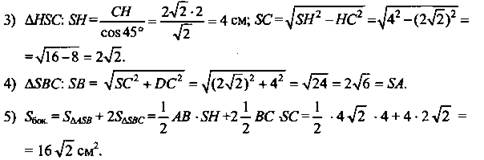
(Ответ:
)№ 3. Дано: ABCDA1B1C1D1 - куб: АВ = а.
Построить: сечение МВ1СК.
Найти: SМВ1СК.
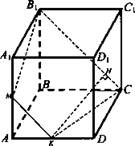
Решение:
1) По свойству секущей плоскости МК || В1С, тогда МВ1СК - искомое сечение.
2) МВ1 = КС, МВ1СК - равнобокая трапеция;
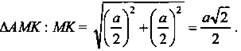
3)
4) ΔKDC - прямоугольный.
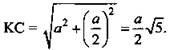
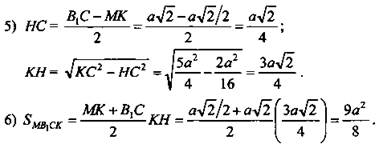
(Ответ:
)III уровень
Вариант I
№ 1. Дано: ABCA1B1C1 - прямоугольная призма; ΔABC: ∠C = 90°; AC = 20 см; ВС = 15 см; SС1H1HC - наименьшее сечение, проходящее через боковое ребро - квадрат.
Найти: Sполн.
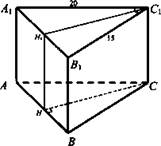
Решение:
1)
2) C1H1 – меньшая высота в ΔA1B1C1;
3)
(Ответ: 1020 см2.)№ 2. Дано: SABCD - пирамида; ABCD - ромб; ∠A = α; АС = d; ∠SHO = β.
Найти: Sполн.
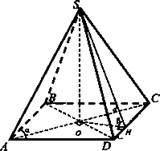
Решение:
1) ΔAOD - прямоугольный:
2) ΔOCH - прямоугольный:
ΔOSH - прямоугольный: 
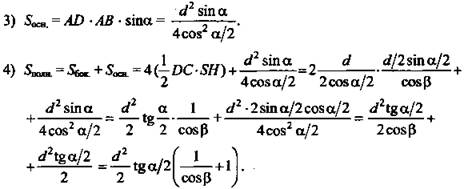
(Ответ :
)№ 3. Дано: ABCDA1B1C1D1 - куб; AB = а; M, К, P - середины ребер AA1, B1C1, CD) соответственно.
Построить: сечение, проходящее через точки М, К, Р.
Найти: Sсeч.
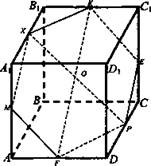
Решение: 1) МХ || PF (так как секущая плоскость пересекает противоположные грани по параллельным отрезкам). Значит,MF || КЕ, ХК || FP. Тогда MXKEPF - правильный шестиугольник:
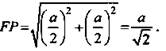
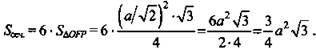(Ответ: 
)Вариант II
№ 1. Дано: ABCDA1B1C1D1 - прямая призма. ΔАВС: АС = ВС = 13 см; АВ = 24 см. НН1С1С - квадрат - наименьшее сечение призмы, проходящее через боковое ребро.
Найти: Sполн.
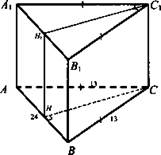
Решение:
1) ΔНВС - равнобедренный.
HC = CC1 = 5 см.2)
(Ответ: Sполн. = 370 см2.)№ 2. Дано: ABCD - ромб; SABCD - пирамида; ∠B = α; ∠SHO = β; SO = Н;
Найти: Sполн.
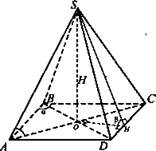
Решение:
1) ΔSOH - прямоугольный;
2) ΔHOD - прямоугольный;
3) ΔODC - прямоугольный;
4) ΔDOC - прямоугольный;
(Ответ: 
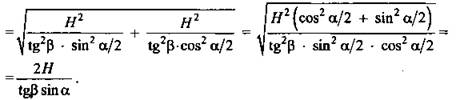
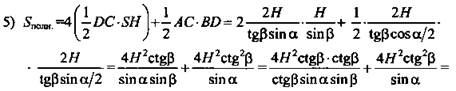
)№ 3.
Аналогично № 3, вариант 1. (Ответ:
)