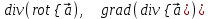Файл: Контрольная работа по дисциплине Дополнительные главы Высшей математики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа по дисциплине «Дополнительные главы Высшей математики»
При выполнении работы студент должен проставить вместо резервированных буквенных параметров индивидуальные анкетные характеристики:
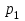 - число букв в полном имени студента,
- число букв в полном имени студента, 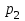 - число букв в полном имени отца студента,
- число букв в полном имени отца студента, 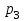 - число букв в фамилии студента. При отсутствии каких-либо анкетных характеристик соответствующее значение параметра следует принимать равным 1. Работу следует выполнить аккуратно. В каждом примере указать тип (название) интеграла.
- число букв в фамилии студента. При отсутствии каких-либо анкетных характеристик соответствующее значение параметра следует принимать равным 1. Работу следует выполнить аккуратно. В каждом примере указать тип (название) интеграла. -
Вычислить интеграл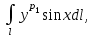 где
где 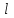 - участок кривой
- участок кривой 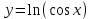 между точками
между точками 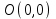 и
и 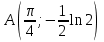 .
. -
Вычислить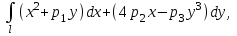 где
где 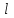 - ломаная АВС:
- ломаная АВС: 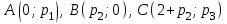 .
. -
С помощью формулы Остроградского-Грина вычислить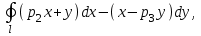 где
где 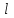 - эллипс
- эллипс 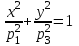
-
Вычислить криволинейный интеграл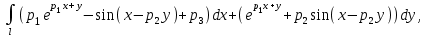 вдоль кривой от точки
вдоль кривой от точки 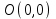 до точки
до точки 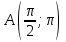
-
Найти работу силы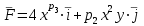 вдоль кривой
вдоль кривой 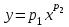 от точки
от точки 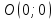 до точки
до точки 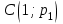
-
Найти массу части поверхности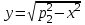 , отсеченной плоскостями
, отсеченной плоскостями 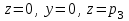 с поверхностной плоскостью
с поверхностной плоскостью 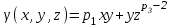
-
Вычислить интеграл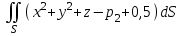 , где
, где 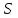 - часть поверхности
- часть поверхности 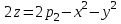 , отсеченная плоскостью
, отсеченная плоскостью 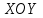
-
Вычислить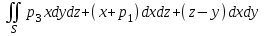 , где
, где 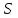 -внешняя часть поверхности
-внешняя часть поверхности 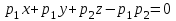 , находящаяся в первом октанте
, находящаяся в первом октанте -
С помощью формулы Остроградского-Гаусса вычислить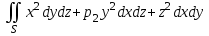 , где
, где 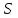 - полная поверхность конуса
- полная поверхность конуса 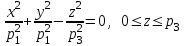
-
С помощью формулы Стокса вычислить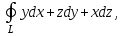 где
где 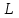 - окружность
- окружность 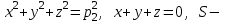 часть плоскости
часть плоскости 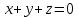 , ограниченная данной окружностью.
, ограниченная данной окружностью. -
Проверить, является ли векторное поле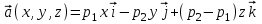 потенциальным, соленоидальным, гармоническим. Если поле потенциально, то найти потенциал поля. Если поле – гармоническое, то найти оператор Гамильтона
потенциальным, соленоидальным, гармоническим. Если поле потенциально, то найти потенциал поля. Если поле – гармоническое, то найти оператор Гамильтона 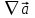
-
Дано векторное поле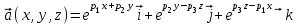 . Необходимо найти
. Необходимо найти