Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования Санкт-Петербургский горный университет Кафедра транспорта и хранения нефти и газа Рассчетно-графическое задание №1 По дисциплине: Основы газового дела ^{(наименование учебной дисциплины, согласно учебному плану)} Тема работы: Расчет газовых смесей

Выполнил: студент гр.	ГРП-21			Лысенко А.И.
	(шифр группы)	(подпись)		(Ф.И.О)
Оценка:
Дата: Проверил
руководитель работы:				Духневич Л.Н.
	(должность)	(подпись)		(Ф.И.О)

Санкт-Петербург 2023 Теоретическая частьГазовая смесь – это смесь отдельных газов, не вступающих между собой в химическое взаимодействие.Природный газ – смесь низкомолекулярных углеводородов, основным компонентом которой является метан, добываемая из осадочных пород Земли.Наиболее частой смесью является воздух, состоящий из азота, кислорода, и прочих примесей, а так же природный газ, в состав которого входят предельные и непредельные углеводороды, азот и другие примеси. Газовые смеси подразделяются на следующие виды: поверочные и градуированные

---

, технические, пищевые, смеси для стерилизации, эксимерные смеси.

В результате процесса горения топлива также получается газовая смесь. Состав этой смеси, или продуктов сгорания топлива, может быть самым разнообразным и зависит как от состава топлива, так и от условий, при которых происходит процесс сгорания (в частности, от количества подводимого воздуха).

Газовые смеси рассматриваются как идеальные газы и подчиняются законам идеальных газов. Уравнением состояния для них служит уравнение Менделеева — Клапейрона. Главным принципом, определяющим свойства газовой смеси, является принцип независимости действия газов в смеси, то есть каждый газ в смеси действует независимо. Следует только иметь в виду, что в формулы для решения задач подставляются значения молекулярной массы смеси, газовой постоянной смеси, объема и давления смеси.

Решение задач на газовые смеси сводится, главным образом, к определению массовых и молярных концентраций компонентов (m_i, r_i), определению средней молекулярной массы смеси (µ_i), теплоемкостей смеси, газовой постоянной, средней температуры смеси, что позволяет судить о составе и дать качественную и количественную характеристику газовой смеси.

Условие задачи

По данным объемного состава природного газа(Вариант 1):

СН₄ = 90,0 %; С₂Н₆ = 8,0 %; С₃Н₈ = 0,6 %;

С₄Н₁₀ = 0,4 %; СО₂ = 0,2 %; N₂ = 0,8 %,

определить среднюю молекулярную массу природного газа, плотность газа в нормальных условиях, массовые концентрации компонентов, их парциальные давления, средние теплоемкости и показатель адиабаты.
Решение

1. 
   Молекулярные массы составляющие смесь газов равны µ (по данным физических характеристик компонентов газа и таблице Менделеева):
   

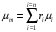
СН₄ = 16,04; С₂Н₆ = 30,07; С₃Н₈ = 44,09;С₄Н₁₀ = 58,12; СО₂ = 44,01; N₂ = 28,02.Молекулярная масса природного газа определяется по уравнению:Зная объемный состав газа, находим его молекулярную массу:

---

2. 
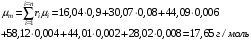
   Плотность газа при нормальных условиях можно определить из закона Авогадро:
   

3. 
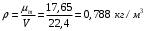
   Массовые и объемные концентрации газа связаны между собой соотношением
   

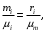
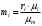
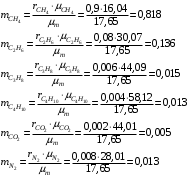
Следовательно:Рассчитаем массовые концентрации компонентов газовой смеси:Округлив до двух значащих цифр, проверим правильность расчета массовых концентраций:

4. 
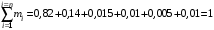
   Парциальные давления отдельных компонентов газа определяются по закону Дальтона из соотношения
   

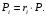
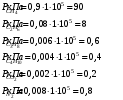
Соответственно, парциальное давление компонентов газа равно:Проверку расчета проведем через закон Дальтона(Общее давление идеального газа равно сумме парциальных давлений его компонентов). Давление газа при нормальных условиях равно 0,1 МПа.

5. 
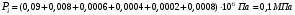
   Средняя теплоемкость подразделяется на массовую и молярную.
   

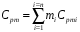
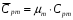
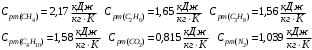
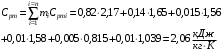
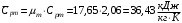
Массовая теплоемкость смеси Молярная теплоемкость смесиПри нормальных условиях теплоемкости компонентов газовой смеси равны:Расчет массовой концентрации при постоянном давлении:Расчет молярной концентрации при постоянном давлении:Теплоемкость смеси газов при постоянном объеме определяется по уравнению Майера (С_p‑С_v=R). Соответственно, массовая и молярная концентрация при постоянном объеме равно:

6. 
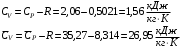
   Используя численные значения теплоемкостей можно определить показатель адиабаты природного газа:
   

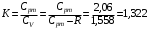
ВыводыГазовая смесь – механическая смесь идеальных газов, не вступающий в химические реакции друг с другом. Компоненты идеального газа занимают весь объем смеси и имеют одинаковую температуру. Основной составляющей природного газа является метан (самый распространенный углеводород), а также другие углеводороды, их производные, полученные путем замещения атомов водорода на другие атомы или группы атомов, и прочие мелкие примеси.

---

Пользуясь данным в условии задачи объемным составом были получены количественные характеризующие значения молекулярной массы 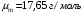, плотности при нормальных условиях 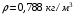, массовые концентрации и парциальные давления каждого отдельного компонента смеси, массовая 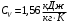и молярная 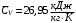концентрация и показатель адиабаты 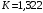газовой смеси.

---

Смотрите также файлы

• Млік абдуллин.docx

• Практическая работа к теме Страна патриотизм Тема занятия День народного единства. Что мы Родиной зовем Класс 5 Опорный конспект разговора о ценности Патриотизм.docx

• Красивый и оригинальный браслет Шамбала является не только неординарным.docx

• 2. 1 Расчет реальных инвестиций Расчет реальных инвестиций на строительство предприятия.docx

• Задача 33876.docx